Visualizzazione di una Curva Cubica Complessa

Ricordiamo che ogni curva cubica complessa non singolare è proiettivamente equivalente ad una cubica di equazione affine Y² = X (X − 1) (X − c), per qualche numero complesso c (diverso da 0 e 1).
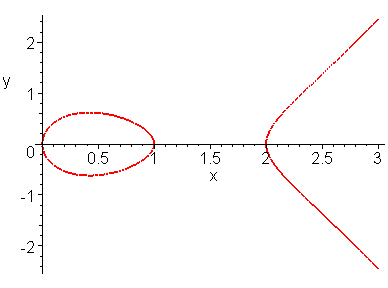Consideriamo, a titolo di esempio, la cubica C di equazione (*) Y² = X (X − 1) (X − 2). L'insieme dei punti del piano affine reale le cui coordinate soddisfano tale equazione è rappresentato nel grafico seguente Grafico cubica

Naturalmente quello che si vede in questo grafico è solamente la parte reale della curva C; ci sono infiniti altri punti che soddisfano l'equazione (*) le cui coordinate sono numeri complessi. Ci poniamo ora il problema di rendere visibile, almeno parzialmente, la parte non reale della curva C.
Consideriamo dunque coordinate complesse ξ e η e poniamo ξ = X + i Y e η = Z + i W, ove X, Y, Z e W sono coordinate reali (e ove i indica una radice quadrata di −1).
L'equazione (*), in coordinate complesse, diventa η² = ξ (ξ − 1) (ξ − 2) la quale, dopo aver sostituito le espressioni ξ = X + i Y e η = Z + i W e dopo aver separato la parte reale da quella immaginaria, si traduce nel seguente sistema di due equazioni nelle quattro indeterminate X, Y, Z e W: Z² − W² − X³ + 3X² + 3XY² − 2X − 3Y² = 0 2ZW − 3X²Y + 6XY + Y³ − 2Y = 0 Queste sono dunque le equazioni della "curva" C in R⁴, nell'identificazione di R⁴ con C² data da (X, Y, Z, W) → (ξ, η). Dal punto di vista reale la curva complessa C è dunque una superficie in R⁴ (cioè ha dimensione 2 sul campo dei numeri reali).
Naturalmente non possiamo visualizzare direttamente un oggetto immerso in uno spazio quadridimensionale! Tuttavia possiamo considerare, ad esempio, la proiezione π : R⁴ → R³, (X, Y, Z, W) → (X, Y, Z) L'immagine della superficie C tramite π è una superficie immersa nell'usuale spazio tridimensionale reale R³; questa può dunque essere visualizzata.
A questo punto il problema che dobbiamo risolvere è quello di determinare l'equazione della superficie π(C) in R³ note le equazioni di C in R⁴. Dato che la proiezione π è definita da π(X, Y, Z, W) = (X, Y, Z), tutto quello che dobbiamo fare è "eliminare" l'indeterminata W dalle equazioni di C (perché?). Ricaviamo dunque W dalla seconda equazione e sostituiamo l'espressione trovata nella prima. Dopo un po' di calcoli si ottiene la seguente equazione: 9X⁴Y² − 36X³Y² + 4X³Z² − 6X²Y⁴ + 48X²Y² − 12X²Z² + 12XY⁴ − 24XY² − 12XY²Z² + 8XZ² + Y⁶ − 4Y⁴ + 4Y² + 12Y²Z² − 4Z⁴ = 0 Il luogo delle soluzioni di questa equazione è dunque la proiezione della curva complessa (cioè della superficie reale) C in R³. Questo luogo geometrico può essere ora facilmente visualizzato con l'ausilio di un calcolatore.
Con il software MAPLE, ad esempio, basta dare i seguenti comandi:

> F := 9*X^4*Y^2 - 36*X^3*Y^2 + 4*X^3*Z^2 - 6*X^2*Y^4 + 48*X^2*Y^2
       - 12*X^2*Z^2 + 12*X*Y^4 - 24*X*Y^2 - 12*X*Y^2*Z^2
       + 8*X*Z^2 + Y^6 - 4*Y^4 + 4*Y^2 + 12*Y^2*Z^2 - 4*Z^4;
> with(plots):
> implicitplot3d( F = 0, X = -2..3, Y = -4..4, Z = -4..4,
       grid = [20,20,20],
       orientation = [-53,70]);

per ottenere il seguente risultato: Grafico cubica 3D

Come si può vedere il risultato non è molto entusiasmante!
Delle immagini molto più dettagliate e realistiche si possono ottenere utilizzando un software di raytracing come, ad esempio, POVRAY.

(cliccare sulle immagini per una versione ad alta risoluzione)

Nell'immagine di sinistra è rappresentata una porzione della superficie π(C). La superficie stessa è parzialmente trasparente, in modo da poter vedere anche le parti nascoste. Si noti la presenza di "autointersezioni"; queste sono dovute alla proiezione π da R⁴ a R³. In realtà la superficie C in R⁴ è non singolare, ma quando essa viene proiettata da R⁴ a R³ due punti che differiscono solo per la coordinata W hanno la stessa immagine; questo genera le "autointersezioni" visibili nelle figure precedenti. La parte della superficie evidenziata in rosso è la sezione reale della curva complessa C (cioè la sezione ottenuta ponendo Y = 0 e W = 0). Questa sezione è precisamente quella mostrata nel primo grafico, all'inizio di questa pagina.
Nella figura di destra, per permettere una visione migliore, è stata rimossa la metà anteriore della superficie (quella corrispondente a Y < 0).
(Per chi fosse interessato, forniamo il codice Povray usato per ottenere le figure precedenti).

Infine, se si hanno a disposizione degli occhiali 3D (quelli con lenti rosse e blu

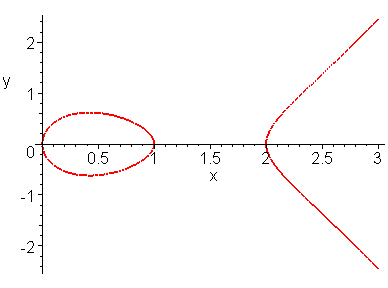
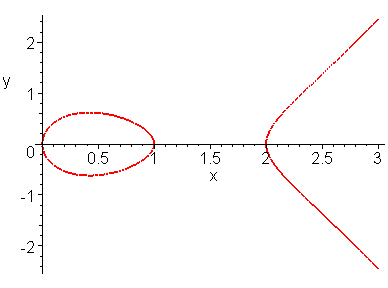
), è possibile vedere una versione tridimensionale (anaglifo) della figura precedente (questo anaglifo è stato ottenuto con il programma Callipygian).