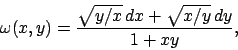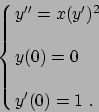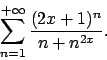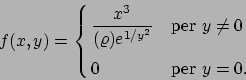Next: About this document ...
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 10.4.2003
- Risolvere il seguente problema di Cauchy:
- Determinare gli estremi della funzione
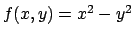 nell'insieme
nell'insieme
- Calcolare il seguente integrale doppio:
dove
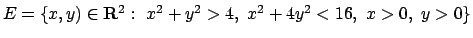 .
.
- Verificare se l'equazione
definisce implicitamente una funzione 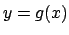 in un intorno
del punto
in un intorno
del punto 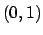 . In caso affermativo, stabilire se
. In caso affermativo, stabilire se 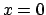 è
punto stazionario di
è
punto stazionario di 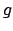 ed eventualmente classificarlo.
ed eventualmente classificarlo.
- Calcolare l'insieme di convergenza della serie
e determinarne la somma.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 4.2.2003
- Risolvere il seguente problema di Cauchy:
- Trovare i punti di massimo e di minimo della funzione
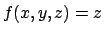 nell'insieme
nell'insieme
- Calcolare il seguente integrale di superficie:
dove
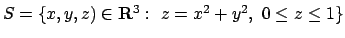 .
.
- Data la funzione
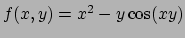 , dire se l'equazione
, dire se l'equazione
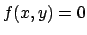 descrive il grafico di una funzione
descrive il grafico di una funzione 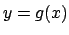 in un intorno
del punto
in un intorno
del punto 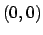 . In caso affermativo, stabilire se
. In caso affermativo, stabilire se 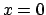 è
punto critico di
è
punto critico di 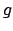 ed eventualmente classificarlo.
ed eventualmente classificarlo.
- Calcolare l'insieme di convergenza della serie
e determinarne la somma.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 14.1.2003
- Risolvere il seguente problema di Cauchy:
- Trovare i punti di massimo e di minimo della funzione
nell'insieme
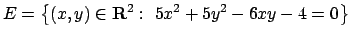 .
.
- Sia
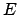 l'intersezione dei cerchi di centri (-1,0) e (1,0)
e raggio
l'intersezione dei cerchi di centri (-1,0) e (1,0)
e raggio 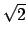 . Calcolare
. Calcolare
- Data la forma differenziale
dire se essa è esatta e, in caso affermativo, determinarne le primitive.
- Sviluppare in serie di McLaurin la funzione
e determinare l'insieme di convergenza della serie ottenuta.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 17.12.2002
- Risolvere il seguente problema di Cauchy:
- Calcolare il seguente integrale triplo:
dove
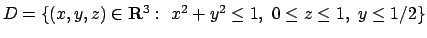 .
.
- Trovare (se esistono) massimo e di minimo assoluti della funzione
nell'insieme
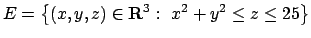 .
.
- Calcolare l'area della superficie ottenuta per rotazione intorno
all'asse
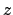 della semicirconferenza:
della semicirconferenza:
- Data la funzione
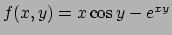 , dire se l'equazione
, dire se l'equazione
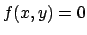 descrive il grafico di una funzione
descrive il grafico di una funzione 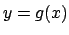 in un intorno
del punto
in un intorno
del punto 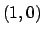 . In caso affermativo, stabilire se
. In caso affermativo, stabilire se 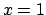 è
punto critico di
è
punto critico di 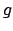 ed eventualmente classificarlo.
ed eventualmente classificarlo.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 29.10.2002
- Risolvere il seguente problema di Cauchy:
- Trovare i punti di massimo e di minimo della funzione
nell'insieme
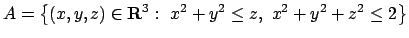 .
.
- Calcolare il volume dell'insieme:
- Data la funzione
stabilire se l'equazione 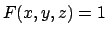 definisce implicitamente una
funzione
definisce implicitamente una
funzione 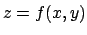 in un intorno del punto
in un intorno del punto 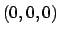 , se
, se 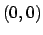 è
punto stazionario per
è
punto stazionario per 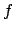 e, in caso affermativo, classificarlo.
e, in caso affermativo, classificarlo.
- Calcolare l'insieme di convergenza della serie
e determinarne la somma.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 10.9.2002
- Risolvere il Problema di Cauchy
- Calcolare il seguente integrale triplo
dove
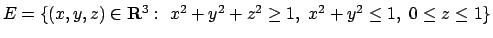 .
.
- Trovare (se esistono) massimo e minimo assoluti della funzione
nell'insieme
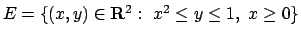 .
.
- Data la funzione
stabilire se l'equazione 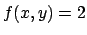 definisce implicitamente una
funzione
definisce implicitamente una
funzione 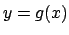 in un intorno del punto
in un intorno del punto 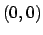 , se
, se 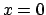 è
punto stazionario per
è
punto stazionario per 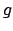 e, in caso affermativo, classificarlo.
e, in caso affermativo, classificarlo.
- Sviluppare in serie di Fourier di soli seni la funzione 2-periodica definita in
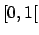 da
da
e precisare gli intervalli di convergenza puntuale e uniforme della serie
ottenuta.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 23.7.2002
- Risolvere il Problema di Cauchy
- Trovare i punti di massimo e di minimo della funzione
nell'insieme
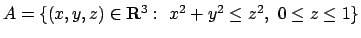 .
.
- Calcolare il seguente integrale:
dove
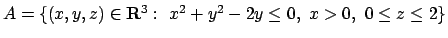 .
.
- Calcolare l'integrale superficiale
dove
- Studiare la convergenza semplice, uniforme e totale della serie
e calcolarne la somma.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 25 Giugno 2002
- Risolvere il Problema di Cauchy
- Calcolare il seguente integrale triplo
dove
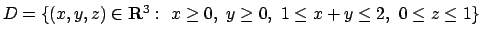 .
.
- Trovare (se esistono) massimo e minimo relativi e assoluti della funzione
nell'insieme
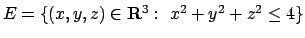 .
.
- Data la forma differenziale
dire se essa è esatta e, in caso affermativo, determinarne le primitive.
- Sviluppare in serie di Fourier la funzione 1-periodica così definita
e precisare il tipo di convergenza.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 14.3.2002
- Risolvere il seguente problema di Cauchy:
- Dato l'insieme
calcolare (se converge) l'integrale doppio
- Determinare (se esistono) la massima e minima distanza
dall'origine dell'insieme
- Stabilire se l'equazione
definisce implicitamente una funzione 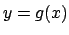 in un intorno del punto
in un intorno del punto
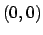 ed eventualmente calcolare
ed eventualmente calcolare
- Determinare gli insiemi di convergenza puntuale, uniforme e
totale della serie di funzioni:
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 4.2.2002
- Risolvere la seguente equazione differenziale:
- Dato l'insieme
calcolare
- Determinare il massimo e il minimo della funzione
nell'insieme
- Studiare la forma differenziale
e, se è esatta, calcolarne le primitive.
- Determinare gli insiemi di convergenza puntuale, uniforme e
totale della serie di funzioni:
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 14.1.2002
- Risolvere il seguente problema di Cauchy:
- Dato l'insieme
calcolare
- Determinare il massimo e il minimo della funzione
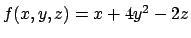 nell'insieme
nell'insieme
- Stabilire se l'equazione
definisce implicitamente una funzione 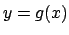 in un intorno del punto
in un intorno del punto
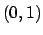 , se
, se 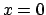 è punto stazionario per
è punto stazionario per 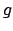 e, in caso affermativo,
classificarlo.
e, in caso affermativo,
classificarlo.
- Determinare gli insiemi di convergenza puntuale, uniforme e
totale della serie di funzioni:
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 10.12.2001
- Calcolare la soluzione del problema di Cauchy:
- Sia
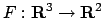 definita da
definita da
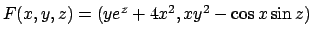 e sia
e sia
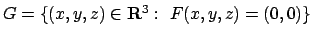 . Dopo aver
verificato che
. Dopo aver
verificato che 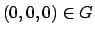 , e che in un intorno di
, e che in un intorno di 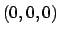 l'insieme
l'insieme
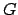 è localmente grafico di un'applicazione
è localmente grafico di un'applicazione
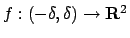 del tipo
del tipo
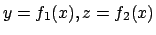 , scrivere la derivata di
, scrivere la derivata di 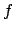 nel punto
nel punto 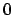 .
.
- Trovare (se esistono) massimo e minimo assoluti della funzione
nell'insieme
- alcolare l'integrale triplo
dove
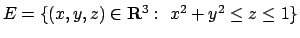 .
.
- Determinare gli insiemi di convergenza puntuale, uniforme e
totale della serie
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 27.11.2001
- Calcolare la soluzione generale dell'equazione differenziale
- Dire se l'equazione
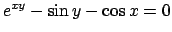 definisce
implicitamente
definisce
implicitamente 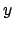 in funzione di
in funzione di 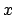 in un intorno di
in un intorno di 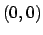 ; in caso
affermativo, calcolare la derivata della funzione
; in caso
affermativo, calcolare la derivata della funzione 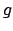 cosí determinata
in
cosí determinata
in 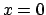 e, qualora
e, qualora 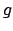 abbia un punto critico in 0, classificarlo.
abbia un punto critico in 0, classificarlo.
- Calcolare massimo e minimo assoluti della funzione
nell'insieme
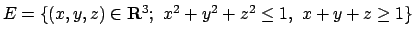 .
.
- Calcolare l'integrale triplo
dove
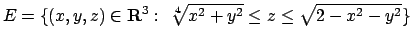 .
.
- Sviluppare in serie di Mac Laurin la funzione:
precisando l'insieme di convergenza.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 17.9.2001
- Calcolare la soluzione del problema di Cauchy:
- Provare che l'equazione
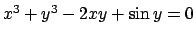 definisce
implicitamente
definisce
implicitamente 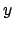 in funzione di
in funzione di 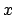 in un intorno di
in un intorno di 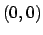 e calcolare
la derivata della funzione cosi' determinata in
e calcolare
la derivata della funzione cosi' determinata in 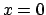 .
.
- Calcolare massimo e minimo assoluti della funzione
nell'insieme
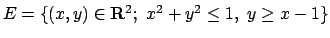 .
.
- Determinare gli insiemi di convergenza puntuale, uniforme e
totale della serie
- Calcolare il volume del solido limitato inferiormente dal piano
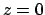 , superiormente dal paraboloide
, superiormente dal paraboloide 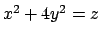 e lateralmente dai
cilindri
e lateralmente dai
cilindri 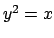 e
e 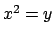 .
.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 16.7.2001
- Calcolare l'integrale generale dell'equazione differenziale
e determinarne la soluzione che verifica la condizione iniziale 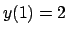 .
.
- Stabilire se esistono valori del parametro
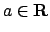 tali che la
forma differenziale
tali che la
forma differenziale
risulti esatta e, per i valori trovati, determinarne le primitive.
- Trovare (se esistono) i punti di massimo e minimo assoluto
della funzione
nell'insieme
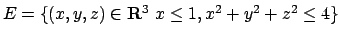 .
.
- Determinare gli insiemi di convergenza puntuale, uniforme e
totale della serie
e calcolarne la somma nel punto 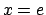 . (Suggerimento: utilizzare
un'opportuna serie di potenze).
. (Suggerimento: utilizzare
un'opportuna serie di potenze).
- Stabilire se esiste l'integrale triplo:
dove
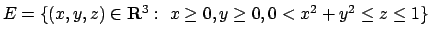 ed eventualmente calcolarlo.
ed eventualmente calcolarlo.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 25.6.2001
- Risolvere il problema di Cauchy
- Calcolare la lunghezza del grafico della funzione
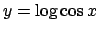 , per
, per
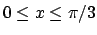 .
.
- Trovare (se esistono) i punti di massimo e minimo assoluto
della funzione
nell'insieme
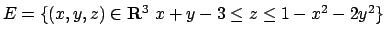 .
.
- Calcolare la somma della serie
precisando l'insieme di convergenza.
- Calcolare il seguente integrale di superficie:
dove 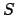 è la porzione di superficie di equazione
è la porzione di superficie di equazione
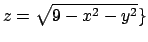 che si proietta sull'insieme
che si proietta sull'insieme
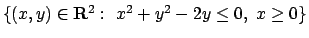 .
.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 4.6.2001
- Determinare tutte le soluzioni dell'equazione differenziale
e, in particolare, dire se fra esse vi sono polinomi.
- Calcolare il volume dell'insieme
- Trovare (se esistono) massimo e minimo assoluti della funzione
nell'insieme
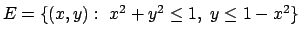 .
.
- Studiare la convergenza puntuale ed uniforme della serie
di funzioni
- Calcolare il seguente integrale di superficie:
dove 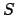 è la porzione della superficie di equazione
è la porzione della superficie di equazione 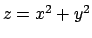 che si
proietta su
che si
proietta su
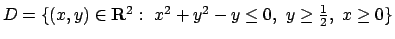 .
.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 19.2.2001
- Determinare tutte le soluzioni limitate dell'equazione
differenziale
- Calcolare l'integrale triplo
dove
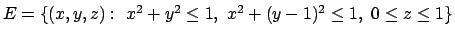 .
.
- Trovare (se esistono) massimo e minimo assoluti della funzione
nell'insieme
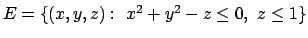 .
.
- Studiare la convergenza puntuale ed uniforme della successione
di funzioni
e dire se vale l'eguaglianza
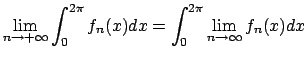 .
.
- Calcolare l'area della seguente superficie:
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 29.1.2001
- Data l'equazione differenziale
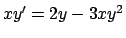 , determinarne
tutte le soluzioni definite in
, determinarne
tutte le soluzioni definite in ![$]0,+\infty[$](img163.png) , quelle definite in
, quelle definite in
![$]-\infty,0[$](img164.png) e dire se vi sono soluzioni definite in
e dire se vi sono soluzioni definite in 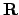 .
.
- Calcolare l'integrale triplo
dove 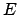 è l'intersezione degli insiemi
è l'intersezione degli insiemi
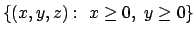 ,
,
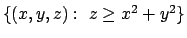 e
e
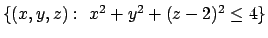 .
.
- Trovare (se esistono) massimo e minimo assoluti della funzione
nell'insieme
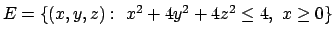 .
.
- Studiare la convergenza puntuale ed uniforme della successione
di funzioni
e calcolare, per ogni ![$c\in]0,1]$](img173.png) , il
, il
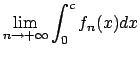 .
.
- Calcolare il seguente integrale di superficie:
dove 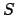 è la parte della superficie di equazione
è la parte della superficie di equazione
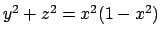 contenuta nel semispazio
contenuta nel semispazio 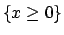 .
.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 15.1.2001
- Determinare (se ne esistono) le soluzioni limitate
dell'equazione differenziale
- Calcolare l'integrale triplo
dove
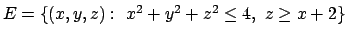 .
.
- Trovare (se esistono) massimo e minimo assoluti della funzione
nell'insieme
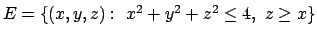 .
.
- Studiare la convergenza puntuale ed uniforme della
serie
- Data la funzione
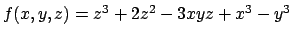 , dire se
l'equazione
, dire se
l'equazione 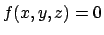 descrive il grafico di una funzione
descrive il grafico di una funzione 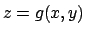 in
un intorno del punto
in
un intorno del punto 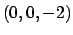 . In caso affermativo, stabilire se
. In caso affermativo, stabilire se 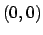 è un punto critico di
è un punto critico di 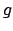 ed eventualmente classificarlo.
ed eventualmente classificarlo.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 18.9.2000
- Determinare la soluzione del problema di Cauchy
- Calcolare massimo e minimo della funzione
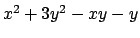 nel quadrato
nel quadrato
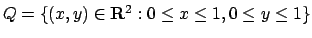 .
.
- Calcolare il seguente integrale doppio
dove
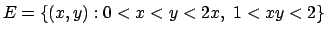 .
.
- Studiare la convergenza della serie
- Assegnata l'equazione
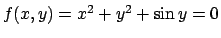 , dire se essa
definisce implicitamente una funzione
, dire se essa
definisce implicitamente una funzione 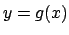 il cui grafico passa per il
punto
il cui grafico passa per il
punto 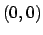 , ed eventualmente dire se in tale punto la funzione
, ed eventualmente dire se in tale punto la funzione 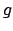 è
crescente, decrescente, ha un estremo relativo o un flesso.
è
crescente, decrescente, ha un estremo relativo o un flesso.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 17.7.2000
- Posto
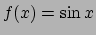 per
per 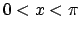 ,
, 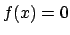 altrimenti,
determinare tutte le soluzioni del problema differenziale
altrimenti,
determinare tutte le soluzioni del problema differenziale
- Calcolare i massimi ed i minimi assoluti della funzione
nell'insieme
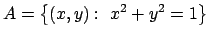 .
.
- Calcolare il seguente integrale doppio (se è convergente)
dove
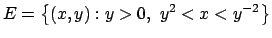 .
.
- Dire se la seguente forma differenziale è esatta nel suo
dominio naturale, e, in caso affermativo, calcolarne le primitive:
- Studiare la convergenza puntuale ed uniforme della
serie
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 26.6.2000
- Data l'equazione differenziale
stabilire se esiste ed è unica la soluzione
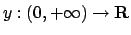 tale che
tale che
- Dato l'insieme
calcolare (se esiste) l'integrale
- Calcolare (se esistono) il massimo e il minimo della funzione
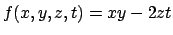 nell'insieme
nell'insieme
- Dato
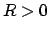 e l'insieme
e l'insieme
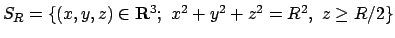 , rappresentare
, rappresentare 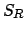 come il
sostegno di una superficie regolare
come il
sostegno di una superficie regolare 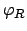 e calcolare l'integrale
superficiale
e calcolare l'integrale
superficiale
- Determinare gli insiemi di convergenza puntuale, assoluta ed
uniforme della serie di funzioni:
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 5.6.2000
- Determinare l'unica soluzione limitata dell'equazione
differenziale
tale che 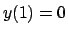 .
.
- Calcolare i massimi ed i minimi assoluti e relativi della
funzione
nell'insieme
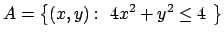 .
.
- Calcolare il seguente integrale doppio (se è convergente)
dove
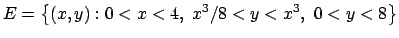 .
.
- Calcolare l'area della porzione del piano
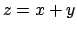 che si
proietta ortogonalmente sulla regione del piano
che si
proietta ortogonalmente sulla regione del piano 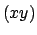 delimitata dalle
rette
delimitata dalle
rette 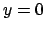 e
e 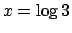 e dalla curva di equazione parametriche
e dalla curva di equazione parametriche
- Studiare la convergenza puntuale ed uniforme della
serie
e calcolarne la somma.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 10.4.2000
- Trovare l'integrale generale dell'equazione
- Calcolare il volume del solido generato dalla rotazione attorno all'asse
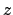 del grafico
del grafico
- Trovare (se esistono) massimo e minimo della funzione
nell'insieme
- Calcolare l'integrale doppio
dove
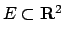 è l'insieme racchiuso dalle rette
è l'insieme racchiuso dalle rette 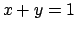 ,
, 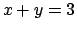 ,
,
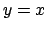 ,
, 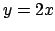 .
.
- Sviluppare in serie di Taylor di punto iniziale
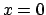 la
funzione
la
funzione
e descrivere l'insieme e il tipo di convergenza della serie ottenuta.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 21.2.2000
- Risolvere il P.d.C.
- Dato l'insieme
stabilire se 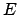 è limitato e calcolarne il volume.
è limitato e calcolarne il volume.
- Trovare (se esistono) i punti dell'insieme
aventi minima o massima distanza dall'origine.
- Dato l'insieme
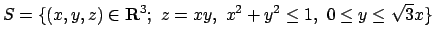 , rappresentare
, rappresentare 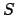 come
il sostegno di una superficie regolare
come
il sostegno di una superficie regolare 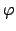 e calcolare l'integrale
superficiale
e calcolare l'integrale
superficiale
- Sviluppare in serie di Fourier la funzione
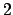 periodica
definita in
periodica
definita in 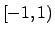 da
da
Precisare gli insiemi di convergenza puntuale ed uniforme.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 13.12.1999
- Trovare la soluzione generale della seguente equazione
differenziale:
- Calcolare il seguente integrale doppio:
dove
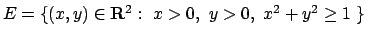 .
.
- Trovare massimi e minimi relativi ed assoluti della funzione
nell'insieme
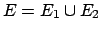 dove
dove
- Data
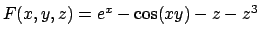 , dire se l'equazione
, dire se l'equazione
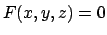 definisce una superficie
definisce una superficie 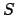 della forma
della forma 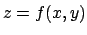 in un
intorno di
in un
intorno di 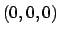 . Verificare che
. Verificare che 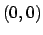 è punto critico di
è punto critico di 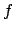 e
classificarlo. È vero che
e
classificarlo. È vero che 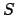 è definita globalmente da
è definita globalmente da 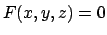 ?
?
- Calcolare la somma della serie:
giustificando i passaggi e precisando l'insieme di convergenza.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 20.9.1999
- Risolvere la seguente equazione differenziale:
- Calcolare il seguente integrale doppio:
dove
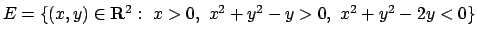 .
.
- Trovare massimi e minimi relativi ed assoluti della funzione
nell'insieme
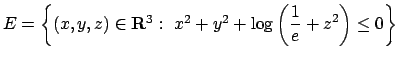 .
.
- Sia
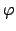 la superficie il cui sostegno è l'insieme
la superficie il cui sostegno è l'insieme
Determinare il versore 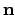 normale alla superficie ed avente la terza
componente positiva e calcolare l'integrale superficiale
normale alla superficie ed avente la terza
componente positiva e calcolare l'integrale superficiale
dove
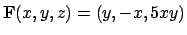 .
.
- Sviluppare in serie di Mac Laurin la funzione:
precisando l'insieme di convergenza.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 6.9.1999
- Trovare la soluzione del seguente problema di Cauchy:
- Sia
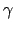 la curva del piano
la curva del piano 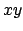 di equazione
di equazione 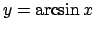 ,
con
,
con ![$x\in [0,1]$](img274.png) , e sia
, e sia 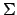 la parte del cilindro con direttrice
la parte del cilindro con direttrice
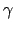 e generatrici parallele all'asse
e generatrici parallele all'asse 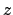 compresa tra i piani
compresa tra i piani 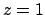 e
e
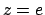 . Calcolare il seguente integrale di superficie
. Calcolare il seguente integrale di superficie
- Trovare massimi e minimi relativi ed assoluti della funzione
nell'insieme
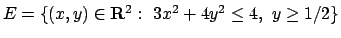 .
.
- Posto
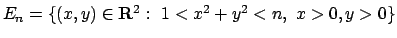 ed
ed
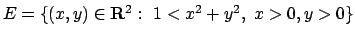 , dire se valgono le seguenti
uguaglianze:
, dire se valgono le seguenti
uguaglianze:
- Calcolare la somma della serie
precisando l'insieme di convergenza puntuale; discutere anche la
convergenza uniforme e totale.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 19.7.1999
- Per ogni valore di
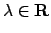 si trovi la soluzione in
si trovi la soluzione in
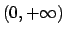 del seguente problema di Cauchy:
del seguente problema di Cauchy:
Si dica se esistono valori di 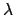 per i quali la soluzione
corrispondente abbia un estremo relativo per
per i quali la soluzione
corrispondente abbia un estremo relativo per 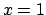 , e si precisi, per
i valori trovati, se si tratta di un massimo o di un minimo.
, e si precisi, per
i valori trovati, se si tratta di un massimo o di un minimo.
- Calcolare il seguente integrale triplo
dove
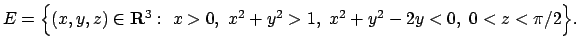
- Trovare massimi e minimi relativi ed assoluti della funzione
- Trovare per quali valori di
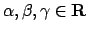 la
forma differenziale
la
forma differenziale
è esatta, e in caso affermativo calcolarne tutte le primitive.
- Data la successione di funzioni
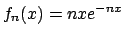 ,
, 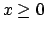 , dire se converge puntualmente, uniformemente e in
, dire se converge puntualmente, uniformemente e in 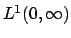 .
.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 7.6.1999
- Scrivere in forma esplicita la soluzione del seguente
problema di Cauchy:
- Calcolare il seguente integrale doppio
dove
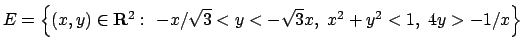 .
.
- Trovare massimi e minimi assoluti della funzione
in
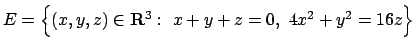 .
.
- Trovare per quali valori di
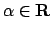 la forma
differenziale
la forma
differenziale
è esatta, e in caso affermativo calcolarne tutte le primitive.
- Assegnata l'equazione
 , dire se
, dire se
- a)
- essa definisce implicitamente una funzione
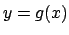 il cui
grafico passa per il punto
il cui
grafico passa per il punto 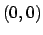 ;
;
- b)
- la funzione
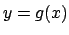 è crescente o decrescente in un
intorno del punto
è crescente o decrescente in un
intorno del punto 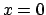 .
.
- c)
- la funzione
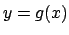 è convessa o concava in un
intorno del punto
è convessa o concava in un
intorno del punto 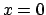 .
.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 17.5.1999
- Risolvere il seguente problema di Cauchy:
- Calcolare il seguente integrale
ove
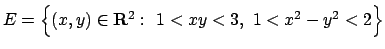 .
.
- Trovare massimi e minimi assoluti della funzione
nel rettangolo di vertici (1,0), (0,1), (-2,-1), (-1,-2).
- Dire per quali valori di
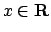 converge la seguente serie,
e calcolarne la somma:
converge la seguente serie,
e calcolarne la somma:
- Calcolare l'integrale di superficie
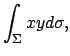 ove
ove
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 11.2.1999
- Risolvere il seguente problema di Cauchy:
- Calcolare il volume dell'insieme
- Trovare massimi e minimi assoluti della funzione
nel sottoinsieme del piano delimitato dalle rette 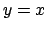 ,
, 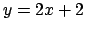 e
e 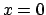 .
.
- Sviluppare in serie di Mac Laurin la seguente funzione:
precisando la convergenza della serie ottenuta.
- Sia
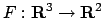 definita da
definita da
e sia
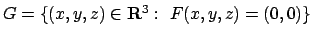 . Dopo aver verificato che
. Dopo aver verificato che
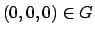 , e che in un intorno di
, e che in un intorno di 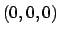 l'insieme
l'insieme 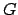 è
localmente grafico di un'applicazione
è
localmente grafico di un'applicazione
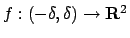 ,
scrivere la matrice jacobiana di
,
scrivere la matrice jacobiana di 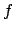 nel punto
nel punto 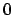 .
.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 14.12.1998
- Determinare tutte le soluzioni della seguente equazione
differenziale
Suggerimento: porre 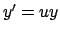 , con
, con 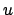 funzione di
funzione di 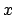 .
.
- Calcolare il seguente integrale
dove
- Trovare massimi e minimi relativi ed assoluti della funzione
in
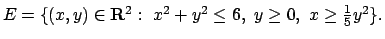
- Calcolare il seguente limite
- Assegnata l'equazione
dire se
- (a)
- definisce implicitamente una funzione
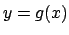 il cui
grafico passa per il punto
il cui
grafico passa per il punto 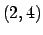 ;
;
- (b)
- la funzione
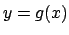 è crescente o decrescente in un
intorno del punto
è crescente o decrescente in un
intorno del punto 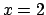 .
.
- (c)
- la funzione
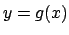 è convessa o concava in un
intorno del punto
è convessa o concava in un
intorno del punto 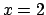 .
.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 30.9.1998
- Determinare le soluzioni del seguente problema di Cauchy
- Calcolare il seguente integrale
dove
- Trovare massimi e minimi relativi ed assoluti della funzione
in
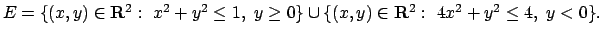
- Calcolare il seguente limite
- Dire se la funzione definita da
è la parametrizzazione di una superficie regolare in un intorno di (1,1),
e, in caso affermativo, scrivere l'equazione del piano tangente nel punto
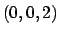 .
.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 8.9.1998
- Determinare l'integrale generale della seguente equazione
differenziale
In che cosa consiste la famiglia delle curve integrali?
- Calcolare il volume del seguente insieme
- Trovare i punti di distanza massima e minima dall'origine
nell'insieme
- Calcolare la lunghezza della curva piana (detta catenaria)
- Verificare che la funzione
è definita in 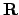 , continua in
, continua in 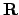 e di classe
e di classe 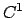 in
in
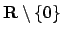 .
.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 20.7.1998
- Determinare tutte le soluzioni del seguente problema
- Calcolare il seguente integrale triplo
dove
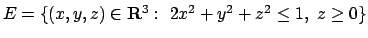 .
.
- Trovare massimi e minimi assoluti della funzione
nell'insieme
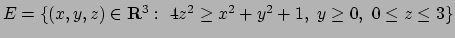 .
.
- Data la forma differenziale
dire se è esatta, e in caso affermativo calcolarne le primitive,
precisando il loro dominio massimale.
- Studiare la convergenza puntuale ed uniforme della serie
e calcolarne la somma.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 22.6.1998
- Risolvere il seguente problema di Cauchy:
e dire qual è il dominio della soluzione.
- Calcolare il seguente integrale triplo
dove
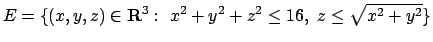 .
.
- Trovare massimi e minimi assoluti della funzione
nel triangolo di vertici (2,0), (0,2) e (-2,0).
- Date la forma differenziale
e la curva 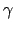 rappresentata parametricamente da
rappresentata parametricamente da
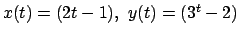 con
con
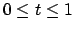 , calcolare il valore dell'integrale
, calcolare il valore dell'integrale
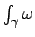 .
.
- Sviluppare in serie di Fourier la funzione 2-periodica
e studiare la convergenza della serie ottenuta.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 25.5.1998
- Risolvere la seguente equazione differenziale:
- Calcolare il volume del solido
- Trovare massimi e minimi assoluti della funzione
nell'insieme
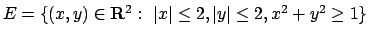 .
.
- Calcolare l'area della figura piana racchiusa dalla curva di
equazioni:
- Sviluppare in serie di soli seni la funzione 4-periodica
definita in
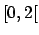 da
da
e studiare la convergenza della serie ottenuta.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 19.2.1998
- Risolvere la seguente equazione differenziale:
- Calcolare l'integrale doppio
ove
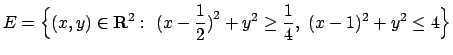 .
.
- Data la curva intersezione della superficie
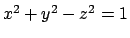 col piano
col piano 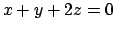 , determinare i suoi punti di quota minima e
massima.
, determinare i suoi punti di quota minima e
massima.
- Studiare la forma differenziale
e, se è esatta, calcolarne le primitive.
- Sviluppare in serie di Mac Laurin la seguente funzione:
precisando la convergenza della serie ottenuta. (Suggerimento:
utilizzare lo sviluppo in serie della derivata di 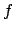 )
)
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 15.12.1997
- Risolvere il seguente problema di Cauchy:
e dire qual è il dominio della soluzione massimale .
- Calcolare l'integrale
ove 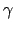 è la curva intersezione della superficie
è la curva intersezione della superficie
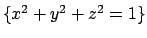 col piano
col piano 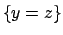 .
.
- Data la curva
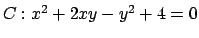 , determinare (se
esistono) la distanza minima e massima dei punti di
, determinare (se
esistono) la distanza minima e massima dei punti di 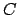 dall'origine.
dall'origine.
- Data
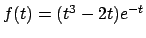 , calcolare
, calcolare
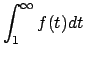 , e dedurre
, e dedurre
- Sviluppare in serie di Mac Laurin la seguente funzione:
precisando la convergenza della serie ottenuta. (Suggerimento:
utilizzare lo sviluppo in serie della derivata di 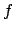 )
)
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 29.10.1997
- Data l'equazione differenziale
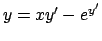 , determinarne
tutte le soluzioni e discutere l'unicità locale e globale delle
soluzioni al variare dei dati iniziali.
, determinarne
tutte le soluzioni e discutere l'unicità locale e globale delle
soluzioni al variare dei dati iniziali.
- Stabilire se l'equazione
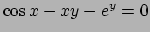 definisce
implicitamente una funzione derivabile
definisce
implicitamente una funzione derivabile 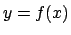 in un intorno del punto
in un intorno del punto
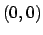 , e, in caso affermativo, scrivere l'equazione della retta tangente
al grafico di
, e, in caso affermativo, scrivere l'equazione della retta tangente
al grafico di 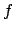 nello stesso punto.
nello stesso punto.
- Determinare (se esistono) estremi assoluti e relativi della
funzione
nell'insieme
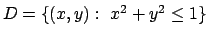 al variare del parametro
al variare del parametro
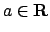 .
.
- Calcolare l'integrale di superficie
dove
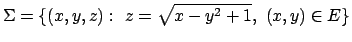 , ed
, ed
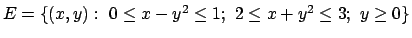 .
.
- Usando la teoria delle serie di potenze, determinare la somma
della serie
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 10.9.1997
- Data l'equazione differenziale
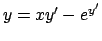 , determinarne
tutte le soluzioni e discutere l'unicità locale e globale delle
soluzioni al variare dei dati iniziali.
, determinarne
tutte le soluzioni e discutere l'unicità locale e globale delle
soluzioni al variare dei dati iniziali.
- Stabilire se l'equazione
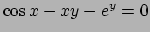 definisce
implicitamente una funzione derivabile
definisce
implicitamente una funzione derivabile 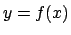 in un intorno del punto
in un intorno del punto
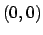 , e, in caso affermativo, scrivere l'equazione della retta tangente
al grafico di
, e, in caso affermativo, scrivere l'equazione della retta tangente
al grafico di 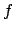 nello stesso punto.
nello stesso punto.
- Determinare (se esistono) estremi assoluti e relativi della
funzione
nell'insieme
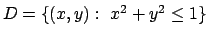 al variare del parametro
al variare del parametro
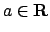 .
.
- Calcolare l'integrale di superficie
dove
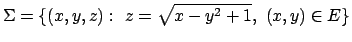 , ed
, ed
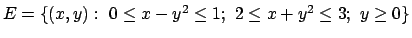 .
.
- Determinare l'insieme di convergenza e la somma della serie
giustificare i passaggi e il significato del risultato.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 21.7.1997
- Una soluzione
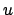 dell'equazione differenziale
dell'equazione differenziale
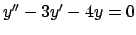 interseca una soluzione
interseca una soluzione 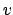 dell'equazione
dell'equazione
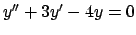 nell'origine. Determinare
nell'origine. Determinare 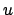 e
e 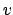 sapendo che hanno la stessa tangente
nell'origine e che
sapendo che hanno la stessa tangente
nell'origine e che
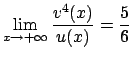 .
.
- Dato il campo vettoriale
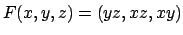 , calcolare
l'integrale
, calcolare
l'integrale
dove 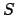 è il rettangolo di vertici
è il rettangolo di vertici 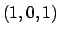 ,
, 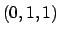 ,
, 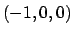 ,
,
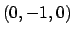 e
e 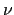 è la normale ad
è la normale ad 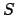 orientata in modo che la
sua componente lungo l'asse
orientata in modo che la
sua componente lungo l'asse 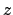 sia positiva.
sia positiva.
- Determinare (se esistono) estremi assoluti e relativi della
funzione
nell'insieme
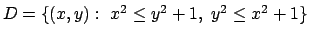 .
.
- Calcolare il volume dell' insieme
- 5 Data la successione di funzioni
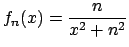 (
(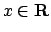 ), studiarne la convergenza, calcolare il
), studiarne la convergenza, calcolare il
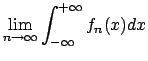 e
verificare l'applicabilità dei teoremi noti sul passaggio al limite
sotto il segno d'integrale.
e
verificare l'applicabilità dei teoremi noti sul passaggio al limite
sotto il segno d'integrale.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 23.6.1997
- Determinare tutte le funzioni che risolvono la seguente
equazione differenziale:
Precisare se esistono soluzioni definite su tutto 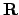 .
.
- Studiare la forma differenziale
e, se è esatta, calcolarne le primitive.
- Determinare (se esistono) estremi assoluti e relativi della
funzione
nell'insieme
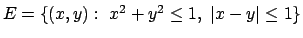 .
.
- Calcolare l'integrale di superficie
dove 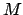 è la superficie generata dalla rotazione del grafico della
funzione
è la superficie generata dalla rotazione del grafico della
funzione 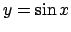 per
per
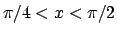 attorno all'asse
attorno all'asse 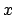 .
.
- Stabilire se esiste finito l'integrale
dove
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 19.5.1997
- Determinare tutte le funzioni che risolvono la seguente
equazione differenziale:
- Studiare la forma differenziale
e, se è esatta, calcolarne le primitive.
- Dire se la funzione
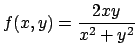 ammette massimo e minimo assoluti nell'insieme
ammette massimo e minimo assoluti nell'insieme
ed eventualmente calcolarli.
- Calcolare l'integrale doppio
dove
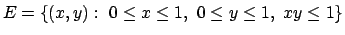 .
.
- Sviluppare in serie di Fourier la funzione
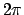 -periodica definita in
-periodica definita in 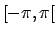 da
da
e studiare la convergenza della serie ottenuta.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 26.2.1997
- Determinare tutte le funzioni che risolvono il seguente
problema:
e calcolare il valore di 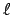 .
.
- Studiare la forma differenziale
e, se è esatta, calcolarne le primitive.
- Determinare (se esistono) estremi assoluti e relativi della
funzione
nell'insieme
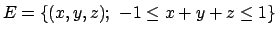 .
.
- Calcolare l'integrale doppio
dove
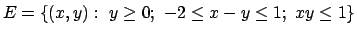 .
.
- 5a) Sviluppare in serie di soli coseni la funzione
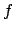 definita nell'intervallo
definita nell'intervallo 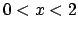 come segue:
come segue:
- 5b) Sia
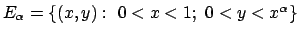 , per
, per
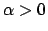 . Data la successione di funzioni
. Data la successione di funzioni
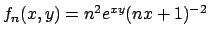 , studiare il
, studiare il 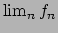 e dire per quali valori di
e dire per quali valori di
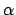 vale l'uguaglianza
vale l'uguaglianza
e per quali valori di 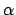 il limite è finito.
il limite è finito.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 17.12.1996
- Risolvere il seguente problema di Cauchy:
- Studiare la forma differenziale
e, se è esatta, calcolarne le primitive.
- Calcolare il massimo e il minimo della funzione
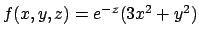
nell'insieme
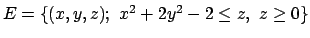 .
.
- Calcolare l'area della superficie
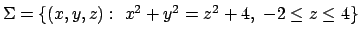 .
.
- 5a) Studiare la convergenza semplice, assoluta, uniforme e totale
della serie
- 5b) Dire se la funzione
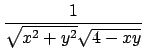 è sommabile
nell'insieme
è sommabile
nell'insieme
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 1.10.1996
- Risolvere il seguente problema di Cauchy
- Sviluppare in serie di soli seni la funzione
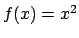 , definita nell'intervallo
, definita nell'intervallo
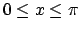 .
.
- Ricercare gli eventuali punti di massimo e minimo assoluto di
nell'insieme
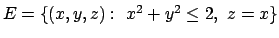 .
.
- Calcolare il seguente integrale
dove
- Data la forma differenziale
determinare i parametri
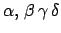 in modo che
in modo che
- a)
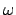 sia chiusa
sia chiusa
- b)
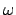 sia esatta; in questo caso calcolarne le primitive.
sia esatta; in questo caso calcolarne le primitive.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 10.9.1996
- Risolvere il seguente problema di Cauchy
Precisare se sono verificate le ipotesi del teorema di esistenza e
unicità e il dominio del prolungamento massimale della soluzione.
- Calcolare la lunghezza della curva definita da
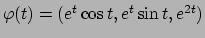 , per
, per ![$t\in [0,1]$](img464.png) .
.
- Calcolare il massimo e il minimo della funzione
nell'
insieme
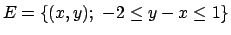 .
.
- Calcolare il seguente integrale
dove
- Determinare una funzione
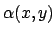 in modo che
la seguente forma differenziale sia esatta:
in modo che
la seguente forma differenziale sia esatta:
e calcolarne le primitive.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 11.7.1996
- Trovare la soluzione del problema di Cauchy:
- Sviluppare in serie di Fourier la funzione
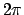 -periodica definita in
-periodica definita in ![$[-\pi,\pi]$](img472.png) da
da
- Determinare massimi e minimi assoluti e relativi della
funzione
nell'insieme
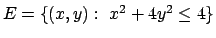 .
.
- Calcolare il seguente integrale doppio:
ove
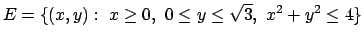 .
.
- Studiare la forma differenziale:
ed eventualmente calcolarne le primitive.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 18.6.1996
- Trovare le soluzioni del sistema differenziale
verificanti le condizioni iniziali 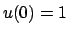 ,
, 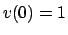 .
.
- Dopo aver studiato la convergenza della successione di
funzioni
calcolare il
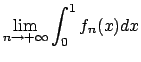 ; si
poteva prevedere il risultato?
; si
poteva prevedere il risultato?
- Determinare massimi e minimi assoluti e relativi della
funzione
nell'insieme
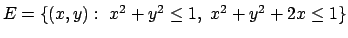 .
.
- Calcolare il seguente integrale doppio:
ove
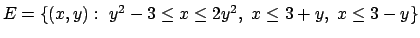 .
.
- Studiare la forma differenziale:
ed eventualmente calcolarne le primitive.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 21.5.1996
- Studiare il seguente problema di Cauchy:
- Sviluppare in serie di Fourier la funzione
- Determinare massimi e minimi relativi della
funzione
nell'insieme
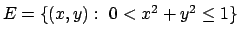
- Calcolare l'area della superficie
interna al solido
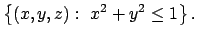
- Dire per quali valori del parametro
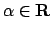 la
forma differenziale è esatta:
la
forma differenziale è esatta:
per i valori trovati calcolare le primitive.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 13.10.1995
- Studiare la convergenza puntuale, uniforme e totale della serie
- Determinare il massimo volume di un parallelepipedo avente superficie
totale
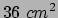 .
.
- Determinare l' integrale generale dell' equazione differenziale
Discutere il comportamento delle soluzioni per 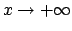 e per
e per
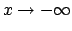 .
.
- Calcolare il seguente integrale
dove
- Studiare la forma differenziale
e calcolare l' integrale
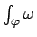 dove
dove 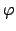 é il bordo del triangolo di vertici
é il bordo del triangolo di vertici
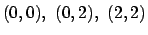 percorso in verso antiorario.
percorso in verso antiorario.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 18.9.1995
- Studiare la convergenza puntuale, uniforme e totale
della serie
- Calcolare il volume del solido:
Suggerimento: utilizzare le proprietà di simmetria di 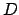 .
.
- Determinare, se esistono, il massimo e il minimo
della funzione
nella striscia
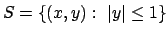 .
.
- Determinare l'integrale generale dell'equazione
differenziale
- Studiare, al variare del parametro
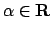 , la
continuità e la differenziabilità della funzione:
, la
continuità e la differenziabilità della funzione:
nei punti dell'asse 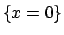 .
.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 21.7.1995
- Studiare la convergenza puntuale, uniforme e totale della
seguente serie:
- Trovare tutte le soluzioni dell'equazione
differenziale
e rispondere ai seguenti quesiti:
- a)
- Esistono soluzioni definite in tutto
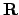 ?
?
- b)
- Esistono soluzioni
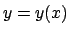 tali che
tali che
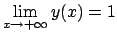 ?
?
- c)
- Esistono soluzioni
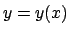 tali che
tali che 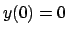 ?
?
- Stabilire se esistono valori del parametro
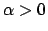 tali che la funzione
tali che la funzione
sia continua e differenziabile nei punti dell'asse 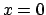 .
.
- Calcolare il seguente integrale:
dove
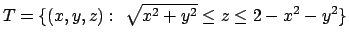 .
.
- Cercare eventuali punti di massimo e di minimo della
funzione
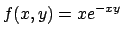 nell'insieme:
nell'insieme:
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 28.6.1995
- Determinare la serie di Fourier della funzione 4-periodica
definita da
Precisare il tipo di convergenzea della serie trovata e di quella
ottenuta da essa derivando termine a termine.
- Calcolare, se esiste,
dove
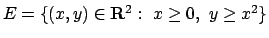 .
.
- Individuare, se esistono, i punti dell'insieme
aventi distanza dall'origine minima o massima.
- Risolvere il problema di Cauchy:
Precisare l'intervallo di definizione del prolungamento massimale
della soluzione.
- Stabilire se esiste
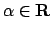 tale che la forma
differenziale
tale che la forma
differenziale
sia esatta; in tal caso determinare le primitive.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 5.6.1995
- Studiare la continuità della funzione
Dire se la funzione ha derivate direzionali ed è differenziabile
nell'origine.
- Trovare l'integrale generale della seguente equazione
differenziale
e rispondere ai seguenti quesiti:
- a)
- Esistono soluzioni
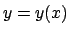 tali che
tali che
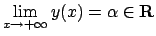 ?
?
- b)
- Esistono soluzioni
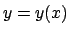 tali che
tali che
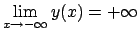 ?
?
- Studiare la convergenza puntuale, uniforme e totale della
seguente serie:
- Dire se la funzione
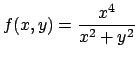 ammette massimo e minimo assoluto nell'insieme:
ammette massimo e minimo assoluto nell'insieme:
e in caso affermativo determinarli.
- Calcolare il seguente integrale:
dove
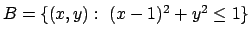 .
.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 9.2.1995
- Studiare la convergenza puntuale, uniforme e totale della serie
- Assegnata la funzione
individuare i punti di minimo e di massimo nell' insieme
- Studiare il seguente problema di Cauchy
e stabilire se esistono valori di 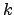 per cui
per cui
- Calcolare al variare di
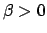 il seguente integrale
il seguente integrale
dove
- Studiare la forma differenziale
e calcolare l' integrale
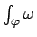 dove
dove 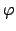 è la circonferenza
è la circonferenza
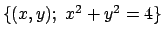 percorsa in verso antiorario.
percorsa in verso antiorario.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 15.12.1994
- Determinare la serie di Fourier della funzione 4-periodica
definita da
- Assegnata la funzione
calcolarne il minimo ed il massimo sulla curva intersezione del piano
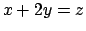 con l'ellissoide
con l'ellissoide
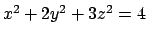 .
.
- Determinare la soluzione del problema di Cauchy
- Calcolare il volume dell' insieme
ed il seguente integrale
Precisare il significato meccanico del rapporto 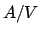 .
.
- Calcolare l' integrale
dove 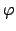 è la frontiera del triangolo di vertici
è la frontiera del triangolo di vertici 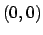 ,
,
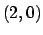 e
e 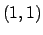 percorsa in verso antiorario.
percorsa in verso antiorario.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 19.9.1994
- Studiare, al variare del parametro
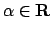 , la
convergenza puntuale, uniforme e totale della serie di potenze
, la
convergenza puntuale, uniforme e totale della serie di potenze
- Assegnata la funzione
stabilire se esiste un prolungamento continuo di 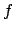 definito su tutto
definito su tutto
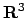 .
.
Stabilire se esiste un prolungamento differenziabile di 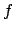 definito su
tutto
definito su
tutto 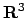 .
.
Determinare, se esistono, il massimo e il minimo della funzione 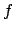 nel suo dominio.
nel suo dominio.
- Determinare una soluzione del problema di Cauchy
precisando se essa è l'unica.
- Calcolare il seguente integrale
dove
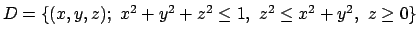 .
.
- Calcolare l' integrale
dove 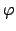 è descritta in figura.
è descritta in figura.
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 27.5.1994
- Studiare, al variare del parametro
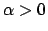 , la convergenza
puntuale, uniforme e totale della serie di funzioni
, la convergenza
puntuale, uniforme e totale della serie di funzioni
- Determinare il massimo e il minimo della funzione
nell' insieme
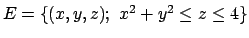 .
.
- Determinare, al variare di
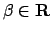 , la soluzione del problema di Cauchy
, la soluzione del problema di Cauchy
precisando il dominio in cui essa è soluzione.
- Calcolare, al variare di
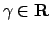 , il seguente
integrale
, il seguente
integrale
dove
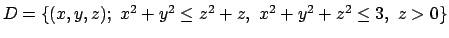 .
.
- Data la curva
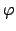 di equazioni parametriche
di equazioni parametriche
Calcolare i seguenti integrali
Facoltà di Ingegneria
Prova scritta di Analisi Matematica II
Lecce, 9.2.1994
- Studiare, al variare del parametro
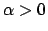 , la
convergenza puntuale, uniforme e totale della serie di funzioni
, la
convergenza puntuale, uniforme e totale della serie di funzioni
- Dire se la funzione
è prolungabile per continuità su  ed individuare, se esistono, i
punti di massimo e di minimo relativo ed assoluto.
ed individuare, se esistono, i
punti di massimo e di minimo relativo ed assoluto.
- Risolvere l'equazione differenziale
Determinare le soluzioni tali che
- a)
-
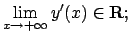
- b)
-
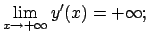
- c)
-
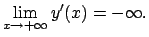
- Calcolare l'ntegrale doppio
dove
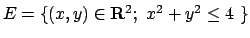 .
.
- Studiare la forma differenziale
Calcolare
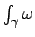 , dove
, dove
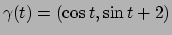 per
per
![$t\in[0,2\pi]$](img588.png) .
.
Prova scritta di Analisi Matematica II
Lecce, 10.1.1994
- Studiare la convergenza puntuale ed uniforme della
successione di funzioni definite su tutto
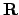 da
da
e calcolare
Rispondere alle stesse domande nel caso
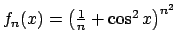 .
.
- Determinare i punti dell'insieme
aventi il valore massimo e il valore minimo di 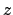 .
.
- Risolvere il problema di Cauchy
precisando
- a)
- se sono verificate le ipotesi del teorema di esistenza e
unicità locale;
- b)
- se sono verificate le ipotesi del teorema di esistenza
globale;
- c)
- per quali valori di
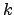 si ottengono soluzioni definite su
tutto
si ottengono soluzioni definite su
tutto 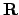 .
.
- Calcolare l'area della porzione di superficie sferica
- Studiare la continuità della funzione
Precisare se la funzione 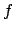 ha le derivate direzionali e se è
differenziabile nei punti del tipo
ha le derivate direzionali e se è
differenziabile nei punti del tipo 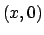 . Dire se
. Dire se
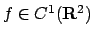 .
.
Prova scritta di Analisi Matematica II
Facoltà di Ingegneria
Lecce, 21.5.1993
- Risolvere il problema di Cauchy:
- Discutere la convergenza puntuale ed uniforme della
seguente successione:
e calcolare
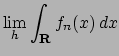 .
.
- Calcolare l'integrale doppio:
ove
- Dire se la funzione
ammette massimo e minimo assoluti nell'insieme
e in caso affermativo calcolarli.
- Studiare la continuità, la differenziabilità, la
continuità delle derivate prime della funzione
Prova scritta di Analisi Matematica II
Facoltà di Ingegneria - Lecce, 4.2.1993
- Studiare il seguente problema di Cauchy:
- Discutere la convergenza puntuale ed uniforme della
seguente serie:
- Calcolare l'integrale doppio
ove
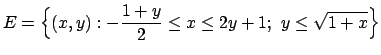 .
.
- Trovare (se esistono) massimo e minimo assoluti della
funzione
nell'insieme
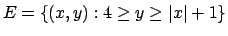 .
.
- Studiare la forma differenziale
e, nel caso che sia esatta, calcolarne le primitive.
Prova scritta di Analisi Matematica II
Facoltà Ingegneria - Lecce, 15.12.1992
- Determinare massimo e minimo della funzione
nell'insieme
- Risolvere il P.d.C.
- Calcolare
sull'insieme
- Studiare la convergenza puntuale, assoluta e uniforme della
serie di funzioni
- Studiare la continuità della funzione
Precisare se la funzione 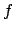 è differenziabile nell'origine.
è differenziabile nell'origine.



Next: About this document ...
Fabio Paronetto
2003-06-18
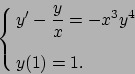
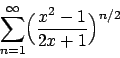
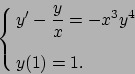
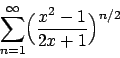
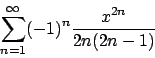
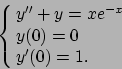
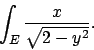
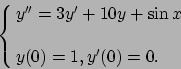
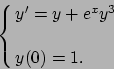
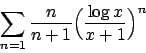
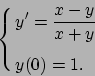
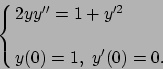
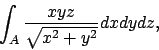
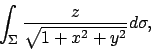
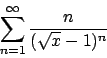
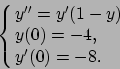
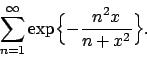
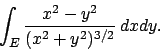
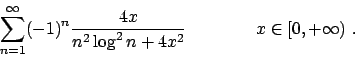
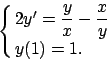
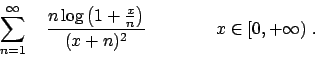
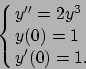
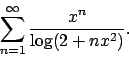
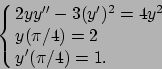
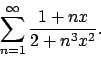
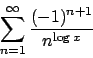
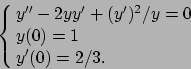
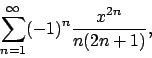
![\begin{displaymath}
\sum_{n=2}^\infty {{(x-1)^n\sin(nx)}\over{n^x}},
\qquad\qquad x\in [1,2].
\end{displaymath}](img150.png)
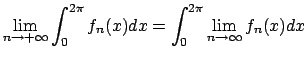 .
.
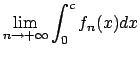 .
.
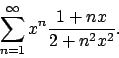
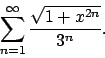
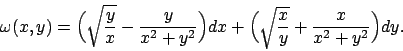
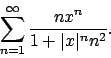
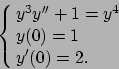
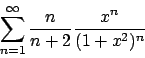
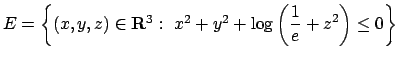 .
.
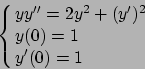
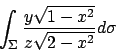
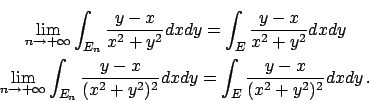
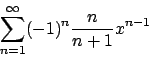
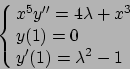
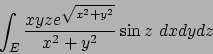
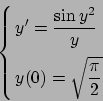
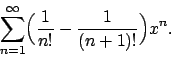
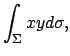 ove
ove
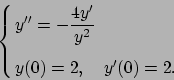
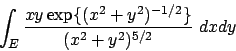
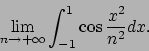
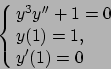
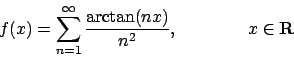
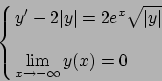
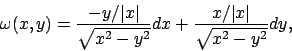
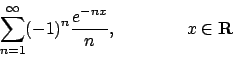
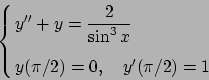
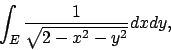
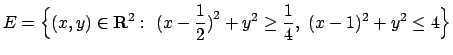 .
.
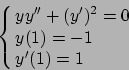
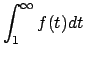 , e dedurre
, e dedurre
 .
.
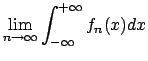 e
verificare l'applicabilità dei teoremi noti sul passaggio al limite
sotto il segno d'integrale.
e
verificare l'applicabilità dei teoremi noti sul passaggio al limite
sotto il segno d'integrale.
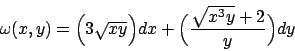
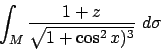
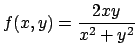 ammette massimo e minimo assoluti nell'insieme
ammette massimo e minimo assoluti nell'insieme
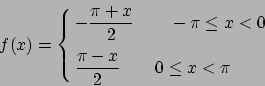
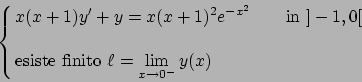
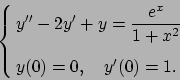
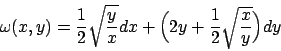
![]() .
.
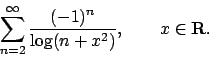
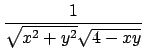 è sommabile
nell'insieme
è sommabile
nell'insieme
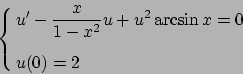
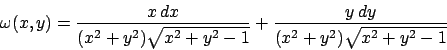
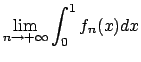 ; si
poteva prevedere il risultato?
; si
poteva prevedere il risultato?
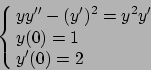
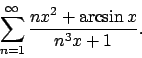
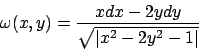

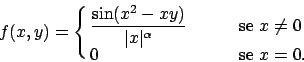
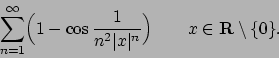
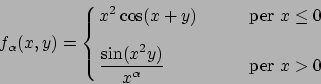
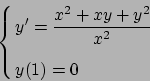
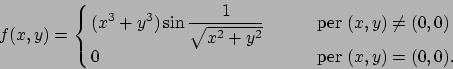
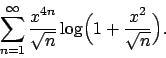
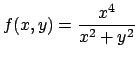 ammette massimo e minimo assoluto nell'insieme:
ammette massimo e minimo assoluto nell'insieme:
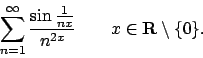
![\begin{displaymath}
\sum_{n=1}^{+\infty} {{x}\over{n^\alpha}}
\Big[\big(1+{1\over n}\big)^\alpha-1\Big] .
\end{displaymath}](img560.png)
![]() definito su
tutto
definito su
tutto ![]() .
.
![]() nel suo dominio.
nel suo dominio.
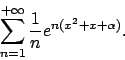

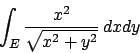
 .
.
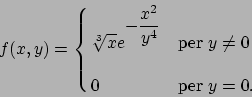
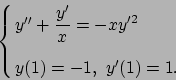
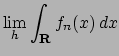 .
.
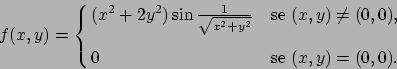
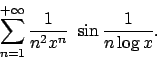
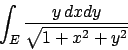
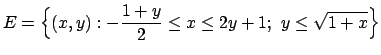 .
.