


Next: About this document ...
Facoltà di Ingegneria
Corso di laurea in Ingegneria dei Materiali, Meccanica e Gestionale
Prova scritta di Matematica 1-Compito A
Lecce, 8 Gennaio 2004
- Tracciare il grafico della funzione così definita
- Studiare il seguente limite
- Calcolare il seguente integrale
- Studiare il carattere della serie
Facoltà di Ingegneria
Corso di laurea in Ingegneria dei Materiali, Meccanica e Gestionale
Prova scritta di Matematica 1-Compito B
Lecce, 8 Gennaio 2004
- Tracciare il grafico della funzione così definita
- Studiare il seguente limite
- Calcolare il seguente integrale
- Studiare il carattere della serie
Facoltà di Ingegneria
Corso di laurea in Ingegneria dei Materiali, Meccanica e Gestionale
Prova scritta di Matematica 1-Compito C
Lecce, 8 Gennaio 2004
- Tracciare il grafico della funzione così definita
- Studiare il seguente limite
- Calcolare il seguente integrale
- Studiare il carattere della serie
Facoltà di Ingegneria
Corso di laurea in Ingegneria dei Materiali, Meccanica e Gestionale
Prova scritta di Matematica 1-Compito D
Lecce, 8 Gennaio 2004
- Tracciare il grafico della funzione così definita
- Studiare il seguente limite
- Calcolare il seguente integrale
- Studiare il carattere della serie



Next: About this document ...
Fabio Paronetto
2004-01-10
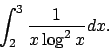
![\begin{displaymath}
\sum_{n=1}^\infty (-1)^n\left(1+\cos\frac{\pi}{\sqrt[n]{5}}\right).\end{displaymath}](img4.png)
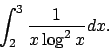
![\begin{displaymath}
\sum_{n=1}^\infty (-1)^n\left(1+\cos\frac{\pi}{\sqrt[n]{5}}\right).\end{displaymath}](img4.png)
![\begin{displaymath}
\sum_{n=1}^\infty (-1)^n\left(1-\sin\frac{\pi}{2\sqrt[n]{2}}\right).\end{displaymath}](img8.png)
![\begin{displaymath}
\sum_{n=1}^\infty (-1)^n\left(\sqrt[n]{3}-1\right).\end{displaymath}](img12.png)
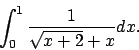
![\begin{displaymath}
\sum_{n=1}^\infty (-1)^n\left(1-\tan\frac{\pi}{4\sqrt[n]{3}}\right).\end{displaymath}](img16.png)