1.    Matrici sparse

Spesso, nelle applicazioni, viene fatto uso di matrici di dimensione n x n, per valori di n molto elevati. Come abbiamo visto, le operazioni con le matrici possono avere complessità di ordine O(n**2) o addirittura O(n**3) per cui esiste un limite fisico, tecnologico, alla dimensione delle matrici trattabili con il calcolatore.

Fortunatamente, le matrici di molte applicazioni risultano avere una grande percentuale di elementi che sono sicuramente uguali a zero. per queste applicazioni è coveniente implementare la matrice come matrice sparsa .

In una matrice sparsa ci sono in genere molte componenti non implementate, e trattate come zeri, e relativamente poche componenti implementate, dette nonzeri. Le prime sono zeri strutturali, le seconde sono valori in generale diversi da zero ma che possono anche essere uguali a zero (zeri accidentali). La disposizione dei nonzeri si dice anche struttura di sparsità della matrice.

Il rapporto tra numero di nonzeri e numero totale di componenti possibili è detto indice di densità, ed è compreso nell'intervallo [0,1]. Una matrice con indice di densità pari a 1 si dice densa .

In Python possiamo agevolmente trattare le matrici sparse mediante l'estensione PySparse  (vedi dispensa).


Esercizio:  costruire un programma Python che si comporti come la funzione "spy()" di Matlab.


Parliamo adesso di occupazione di memoria: quando viene dichiarata una matrice non-sparsa (es. "M = Numeric.zeros((m,n), 'double')"), nella memoria del calcolatore viene riservata un'area di memoria di m*n celle, organizzate in modo da affiancare le m righe di M, avente ognuna n componenti.
Vediamo ora come viene memorizzata una matrice sparsa, ad esempio in formato Compressed Sparse Row (CSR) .  Vengono allocati tre vettori :

• va , di tipo double e di lunghezza nnz , contiene gli elementi nonzeri della matrice, memorizzati riga-per-riga ;
• ia , di tipo integer e di lunghezza nnz , contiene gli indici colonna degli elementi memorizzati in va ;
• ja , di tipo integer e di lunghezza n+1 , contiene gli indici di va (e quindi di ja) che segnalano l'inizio di una nuova riga della matrice . L'ultimo elemento di ja assume il valore nnz+1  . 
  

Facciamo ora un riferimento concreto alle applicazioni: pensiamo di associare ad un grafo con molti nodi e poche connessioni, una matrice di connettività ; ne risulterà una matrice sparsa. Esistono molte applicazioni che richiedono questo tipo di operazione (simulazione di modelli differenziali alle derivate parziali, ...).


Esercizio:  dato un grafo planare, descritto da una certa quantità di nodi, le cui posizioni sono descritte da coppie del tipo "(coord_x, coord_y)", e da una certa quantità di archi bi-direzionali, descritti come coppie "(nodo_A, nodo_B)", scrivere un programma Python (o Matlab/Octave) che disegni il grafo (vertici con "o" e archi con linea), e costruisca la matrice (sparsa) che descrive la connettività del grafo, detta matrice di supporto al grafo (le equazioni corrispondono ai vertici del grafo, ed un "1" in posizione (i,j) significa che esiste un arco tra il nodo i ed il nodo j, mentre tutte le componenti rimanenti sono zeri strutturali).

2.    Il problema del "fill-in" ed algoritmi di pre-ordinamento

Leggere ed eseguire il seguente m-file :    sistemi_sparsi.m  



Esercizio : partendo da una matrice A creata dal precedente m-file , la cui struttura di sparsità è rappresentata nella figura seguente,

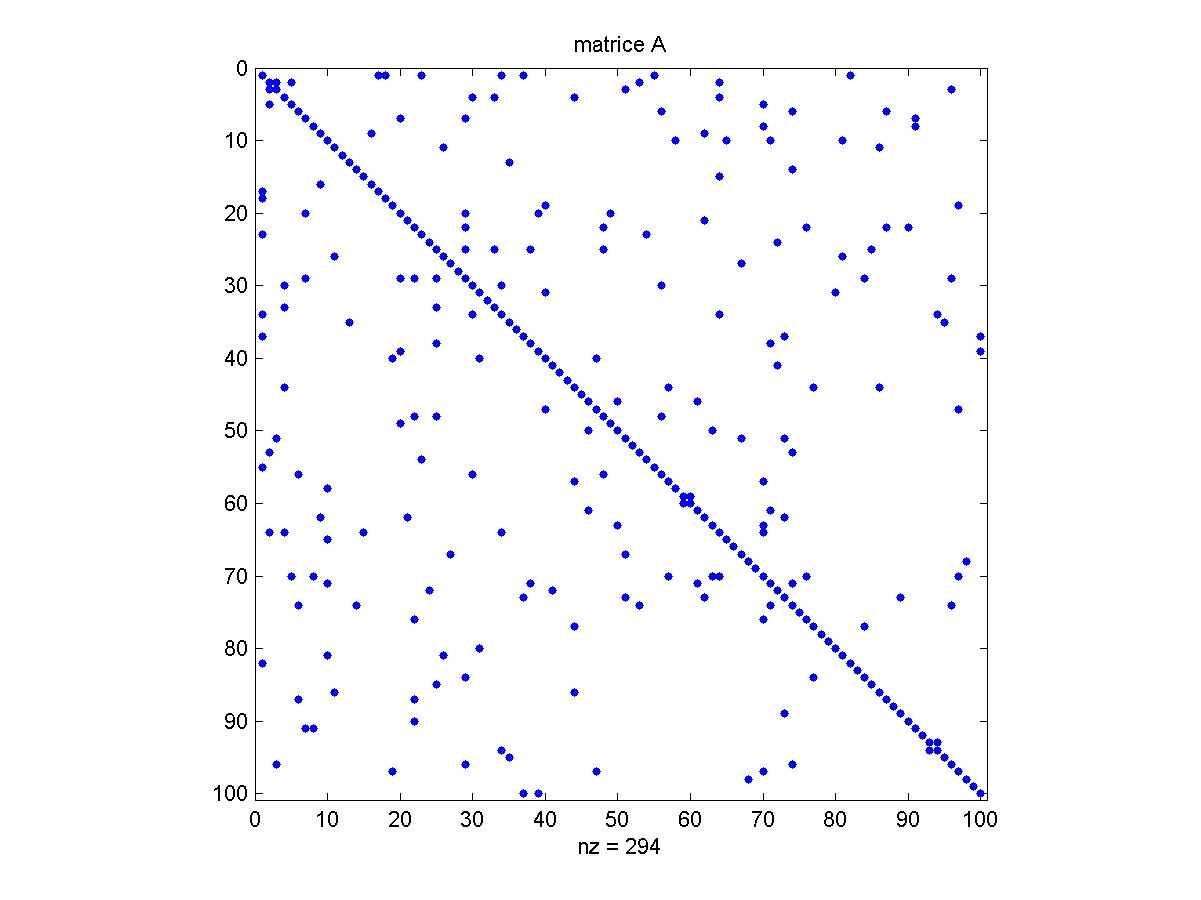
 guarda l'effetto sulla struttura di sparsità stessa creato dal riordinamento con il metodo "Reverse Cuthill-McKee", implementato ad es. nella routine Matlab "symrcm" e mostrato nella figura seguente,

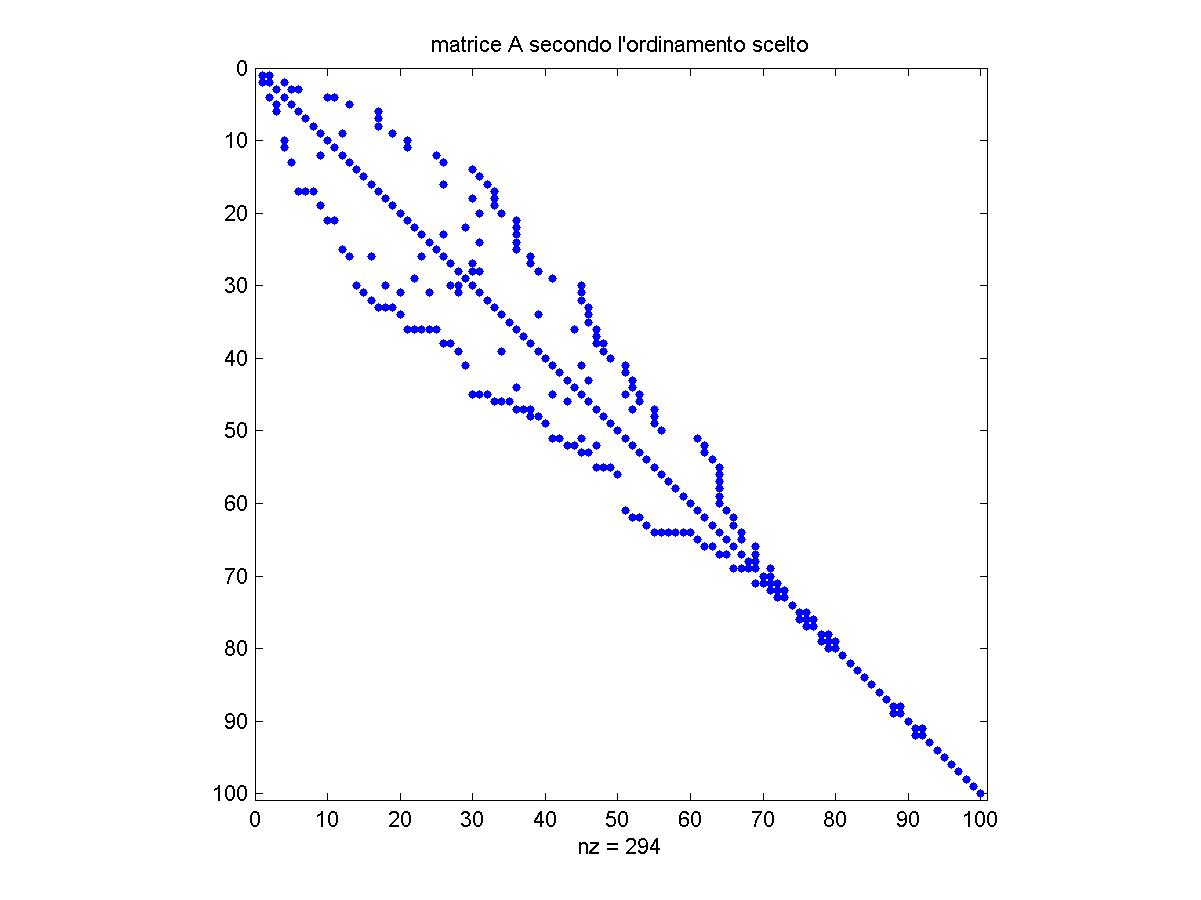
 e poi osserva dove viene aggiunto il fill-in in seguito alla fattorizzazione LU, confrontando la figura precedente con quella seguente (in cui il fill-in è evidenziato in rosso):

Spiegare il motivo di questo comportamento dell'algoritmo di fattorizzazione (cioè perchè il fill-in va a ricoprire proprio la zona indicata in rosso) ?