Gran parte dei problemi del calcolo scientifico ed ingegneristico richiede di risolvere uno o più problemi dell'algebra lineare numerica (ALN) :

• risoluzione di sistemi lineari
• risoluzione di problemi ai minimi quadrati
• ricerca di autovalori e/o autovettori
• calcolo della SVD (valori e vettori singolari)

Inoltre, la risoluzione di questi problemi è generalmente una percentuale considerevole del costo computazionale totale richiesto per la risoluzione del problema globale; questo costo si traduce spesso in ore o giorni di tempo-macchina impiegato. Dunque, implementare in modo efficiente gli algoritmi che risolvono i problemi dell'algebra lineare numerica è estremamente importante dal punto di vista applicativo ed è anche per questo che trattiamo questo caso più approfonditamente.
Un secondo motivo è dovuto al fatto che esistono in rete delle librerie che rappresentano lo stato dell'arte per questi problemi e sono molto ben costruite anche dal punto di vista della implementazione e distribuzione del software numerico: BLAS, LAPACKe ATLAS (disponibili al sito www.netlib.org/blas , /lapack e /atlas).
Vediamo ora la libreria BLAS (Basic Linear Algebra Subroutines).

Gli algoritmi di algebra lineare numerica hanno in comune un insieme relativamente piccolo e stabile di operazioni di base, che svolge la quasi totalità dei calcoli necessari negli algoritmi di ALN. Questo fatto giustifica lo sforzo di creazione di una libreria che implementi queste funzione di base. La libreria BLAS è organizzata in tre livelli:

1. operazioni che lavorano su vettori e producono uno scalare  (es. il prodotto interno, o scalare, tra due vettori colonna: v' * w)
2. operazioni tra vettori e matrici o che comunque producono una matrice (es. il prodotto esterno tra due vettori colonna: v * w')
3. operazioni tra matrici (es. il prodotto di due matrici)
   

Un vantaggio rilevante di aver creato la BLAS è che questa può essere ottimizzata per ogni singola macchina ed in questo modo gli algoritmi di ALN possono diventare "portabili" anche dal punto di vista delle prestazioni di calcolo e non solo da quello della sintassi, semplicemente chiamando le routines della BLAS ove possibile.

Ora, ha senso chiedersi se le operazioni di livello 1, 2 o 3 raggiungono le stesse prestazioni di calcolo. Lo vediamo implementando lo stesso identico algoritmo, il prodotto di due matrici C = A * B, in tre modi diversi, corrispondenti all'utilizzo esclusivo di operazioni di livello 1, di livello 2 e di livello 3.




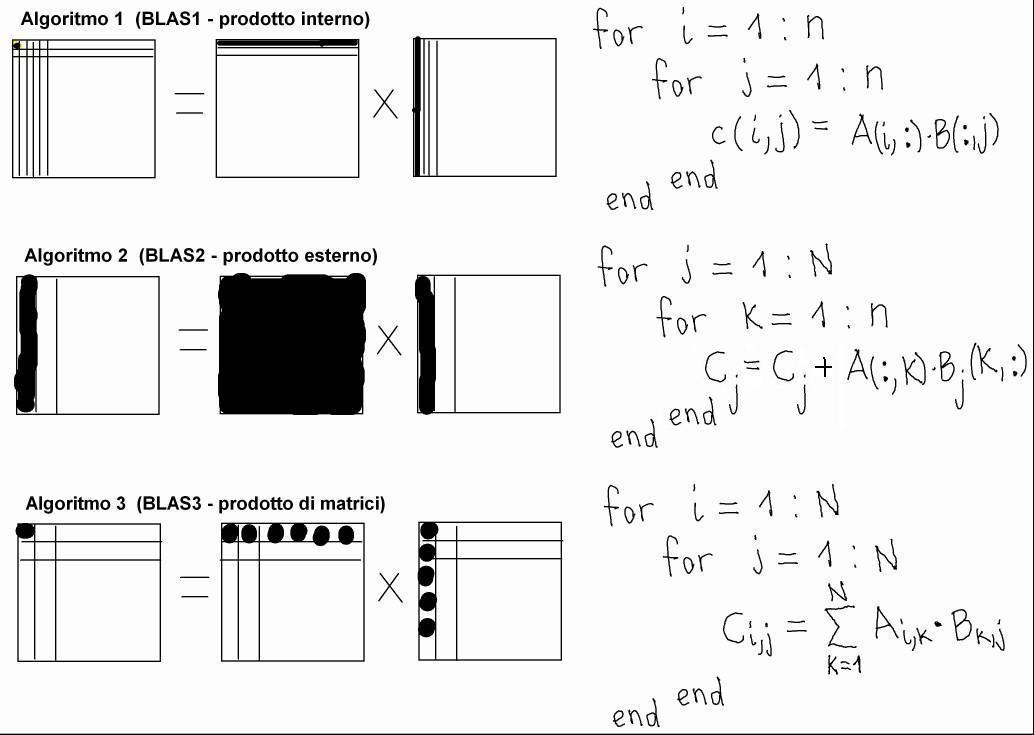
Se facciamo eseguire questi algoritmi da un calcolatore per il quale la libreria BLAS è stata ottimizzata, otteniamo risultati di questo tipo:




e dunque, formulazioni identiche dal punto di vista matematico possono portare a performance molto differenti dal punto di vista delle prestazioni di calcolo. Notare che, in questo esempio, il numero di operazioni in virgola mobile è sempre uguale a 2*n^3 in tutti e tre i casi.
Questo risultato ha validità generale: le operazioni BLAS3 sono molto più veloci delle BLAS2 e BLAS1 nelle macchine di calcolo di ultima generazione, e dunque vanno utilizzate il più possibile negli algoritmi di ALN per avere buone prestazioni dal calcolatore.

Vediamo di spiegare perchè le routines BLAS3 sono più performanti ed in quali condizioni. Una caratteristica sempre più frequente dei problemi di ALN che sorgono nelle applicazioni reali è quella di avere matrici di grandi dimensioni, e dunque una criticità nasce dal punto di vista dell'occupazione di memoria.
Vediamo uno schema dell'organizzazione gerarchica della memoria nei calcolatori attuali (d_s, d_p e d_c indicano il tempo necessario al trasferimento di un'unità di dati):




Lo sviluppo tecnologico delle CPU moderne ha portato a richiedere tempi ridottissimi per l'esecuzione di un'operazione in virgola mobile; non così è stato per la velocità di trasferimento dei dati tra i livelli di memoria: dato che per eseguire un'operazione in virgola mobile la CPU deve poter caricare gli operandi dalla memoria veloce (cache) nei suoi registri e che questa, per ragioni tecnologiche e di costo, ha dimensioni limitate, la criticità maggiore per le prestazioni sul tempo di calcolo è mantenere impegnata la CPU .
In piccola parte il microprocessore ed il compilatore hanno dei mezzi per mascherare i tempi di trasferimento dei dati, ma per ottenere un buon risultato è necessario che l'algoritmo di calcolo e la sua implementazione siano progettati in modo che :


Ora, per le BLAS succede che, detta "n" la dimensione di vettori e matrici (quadrate, per comodità) :

	dati	operazioni
BLAS1	O(n)	O(n)
BLAS2	O(n^2)	O(n^2)
BLAS3	O(n^2)	O(n^3)

e dunque BLAS3, se implementata correttamente, è potenzialmente adatta ad ottenere le migliori prestazioni.

Esiste una misura precisa ed un valore massimo di velocità raggiungibile dalle prestazioni di calcolo. La velocità massima di calcolo raggiungibile da una CPU dipende dalla frequenza di clock, dal numero di cicli di clock necessari ad eseguire un'operazione in virgola mobile (floating-point) e da quante unità hardware per il calcolo f.p. sono presenti. Quindi la velocità massima può essere calcolata dai dati di targa della macchina.
Se il programma prevede una sequenza (lunga) di operazioni in virgola mobile senza istruzioni di altro tipo e se il processore trova sempre disponibili gli operandi nella memoria veloce, il calcolo procede alla massima velocità possibile.
Se il processore non trova disponibili gli operandi nella memoria veloce (cache), deve mettersi in attesa che questi vi arrivino e quindi la sua velocità nell'eseguire calcoli diminuisce. In tal caso, si dice che l'algoritmo non riesce ad utilizzare la macchina in modo efficiente. Vediamo di misurare quantitativamente questa perdita di efficienza.

                                                                                    numero di accessi alla memoria lenta               m                  1
Definiamo come "frazione di perdita", il rapporto :    -------------------------------------------  =  --------  =  ----------
                                                                                   numero totale di accessi alla memoria             2 * f            2 * q

dove " f " è il numero di operazioni in virgola mobile effettuate (si suppone che ogni operazione abbia due operandi), e "q" è il parametro che desideriamo misurare,

                                                                                  f                   numero di operazioni floating-point
definito come                                             q    =    -------    =    --------------------------------------------
                                                                                 m                  numero di accessi alla memoria lenta

Dunque, un algoritmo sarà tanto più efficiente quanto più elevato risulta essere q  .  Cerchiamo ora di valutare q per ognuno dei tre algoritmi precedenti per il prodotto di matrici. Assumeremo per la memoria un modello semplificato: supponiamo due soli livelli di memoria ed i dati vengono trasferiti singolarmente dalla memoria lenta a quella veloce (mentre in realtà i trasferimenti tra cache e memoria principale avvengono per "righe", e tra memoria principale e secondaria avvengono per "pagine"). Per tutti gli algoritmi si ha:    f = 2 * n^3  .
Supponiamo m = mA + mB + mC , cioè scomposto nella somma degli accessi alla matrice A, alla matrice B ed alla matrice C  e calcoliamone il valore. Ispezionando l'implementazione dell'algoritmo, è possibile determinare il numero di accessi effettuati (vedere figura seguente):




Algoritmo 1:     mA = n^2  (accede una volta a ciascuna riga di A)  ,  
                        mB = n*n^2  (accede n volte a ciascuna colonna di B)  ,  
                        mC = n^2  (deposita il risultato per ciascun componente di C).
                        Si ottiene: q  ≈  2

Algoritmo 2:     mA = N*n^2  (accede N volte a ciascuna colonna di A)  ,
                        mB = n^2  (accede una volta a ciascun blocco di colonne di B)  ,
                        mC = n^2  (deposita il risultato per ciascun componente di C).
                        Si ottiene: q  ≈  2 * n / N

Algoritmo 3:     mA = N*n^2  (accede N^2 volte ad un blocco n^2/N di A)  ,
                        mB = N*n^2  (accede N^2 volte ad un blocco n^2/N di B)  ,
                        mC = n^2  (deposita il risultato per ciascun componente di C).
                        Si ottiene: q  ≈  n / N

Notare che:

•  se N=n i tre metodi coincidono (di fatto corrispondono all'Algoritmo 1);
• più piccolo è N e più grande risulta q ;

Fin qui, l'Algoritmo 2 e l'Algoritmo 3 sembrano avere le stesse prestazioni . In realtà, N è limitato dal basso dalla disponibilità di memoria veloce M :

• per l'Algoritmo 2 deve valere M ≥ 2 * n^2/N + n  ,  da cui  N ≥ 2 * n^2 / M  ,  e per il valore minimo possibile di N si ha   q  ≈  M / n
• per l'Algoritmo 3 deve valere M ≥ 3 * n^2/N^2   ,  da cui  N ≥ sqrt ( 3 / M ) * n  ,  e per il valore minimo possibile di N si ha   q  ≈  sqrt ( M / 3 )

Dunque per l'Algoritmo 3 (BLAS3) il valore di q risulta indipendente da n (infatti non c'è nulla di dimensione n da tenere in memoria), e dipende solo dalla quantità di memoria veloce disponibile.
Esiste un Teorema (Hong, Kung ACM 1981) che dimostra che qualsiasi versione a blocchi di questo algoritmo di moltiplicazione di matrici ha  q  ≈  O(sqrt(M))  .

Recentemente è stato portato a termine un progetto molto interessante riguardo alle BLAS: la costruzione di un software che durante la sua esecuzione, genera la libreria BLAS ottimizzata per la macchina su cui è in esecuzione.
Questo software è disponibile gratuitamente al sito :   www.netlib.org/atlas    (attenzione: la sua esecuzione richiede in media due-tre ore su un PC, però funziona in modo completamente automatico e sicuro).
Il suo successo è notevole, dato che riesce ad ottenere ottimizzazioni delle librerie tali da raggiungere le prestazioni ottenute dalle librerie commerciali, ottimizzate "a mano" da esperti.
Provandolo su un PC e confrontandone le prestazioni con le BLAS "generali" scaricate da www.netlib.org/blas si può notare che che la versione "atlas" delle BLAS è decine di volte più veloce delle BLAS "generali", già per una moltiplicazione di matrici di dimensione 1000.
Questo dimostra come le prestazioni di calcolo possono essere ottenute solo sfruttando in maniera sapiente le risorse hardware a disposizione, che possono variare considerevolmente anche solo restando nel mondo del PC (es. un parametro fondamentale è la dimensione della memoria cache).