Sia f una applicazione reale e si supponga sia
nota in ( n+1) nodi distinti xi, i=0,...,n.
Siano f(xi) i valori assunti dalla funzione nei nodi.
Il problema dell'interpolazione polinomiale consiste nel calcolare il
polinomio Pn(x) di grado n tale che siano soddisfatte
le condizioni di interpolazione:
Tale polinomio è chiamato Polinomio di interpolazione di f . Varie sono le rappresentazioni possibili; la più immediata è la forma canonica nella base delle potenze di x:
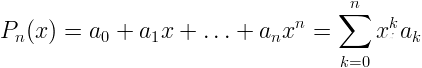
Il problema si riconduce a trovare i coefficienti a0,....,an del polinomio, risolvendo un sistema di (n+1) equazioni in (n+1) incognite ottenuto imponendo le (n+1) condizioni di passaggio per i punti assegnati (metodo dei coefficienti indeterminati):
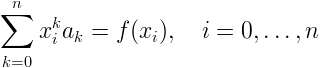
La matrice di tale sistema è la matrice di Vandermonde, non singolare solo se i nodi sono distinti, e in tal caso esiste una ed una sola soluzione, ossia esiste un solo polinomio di interpolazione di grado n.
Tuttavia la matrice di Vandermonde è malcondizionata, pertanto si calcola il polinomio di grado n relativo agli (n+1) punti distinti usando una rappresentazione del polinomio diversa da quella canonica, una di queste rappresentazioni è il Polinomio di Lagrange. Il polinomio di interpolazione può essere scritto mediante la formula di Lagrange:
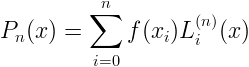
dove l'i-esimo polinomio di Lagrange è dato da
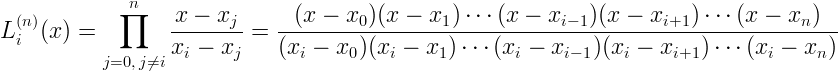
ed è tale che 
, quindi si
verifica che sono soddisfatte le condizioni di interpolazione, infatti
si ha, per j=0,...,n
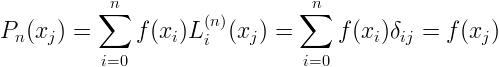
Per osservare le diverse forme di approsimazioni su una serie di dati leggere ed eseguire il seguente m-file: presenta_approssimazione dati, che utilizza la function interLagrange.m
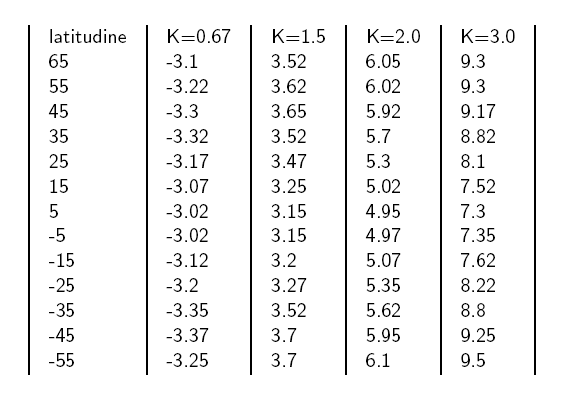
Esercizio 1: utilizzare la seguente tabella relativa ai valori delle variazioni della temperatura media che si riscontrerebbe nel globo rispetto a quella attuale, in corrispondenza di diversi valori della concentrazione K di acido carbonico e della latitudine. (Problema 3.1 del libro di testo)
Costruire il polinomio di interpolazione tramite formula di Lagrange di grado 4 usando 5 nodi della colonna relativa a K=0.67, e il polinomio di grado 12 usando l'intera colonna di dati. Commentare i risultati ottenuti.
Fenomeno di Runge e nodi di Chebychev
Si pensa che il polinomio di interpolazione possa approssimare bene una funzione sopratutto se si aumenta il numero di nodi, in realtà questo non è sempre vero. Utilizzando nodi equispaziati, la distanza tra la funzione f e il polinomio interpolante Pn(x) diminuisce all’aumentare dei nodi fino a quando l’errore di interpolazione risulta maggiore ai bordi dell’intervallo rispetto ai valori assunti al centro. Tale comportamento, detto fenomeno di Runge, si accentua sempre di più all’aumentare del numero di nodi. Il fenoneno di Runge può essere evitato utilizzando opportune distribuzioni di nodi, per esempio i nodi di Chebyshev. Infatti se sull'intervallo [a,b] si considerano i nodi
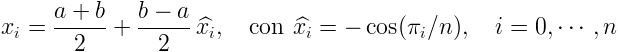
il fenomeno scompare poichè con questa distribuzione di nodi per una qualunque funzione f continua e derivabile con continuità il polinomio interpolante Pn(x) converge ad f per n tendente ad infinito, cioè in modo uniforme.
Per vedere il comportamento dei metodi di interpolazione in un caso notevole, l'esempio di Runge, leggere ed eseguire il seguente m-file: presenta_interp_polinom.m
Esercizio 2: Utilizzare lo script precedente e calcolare per ciascun valore di n (all'interno del ciclo for) nell'interpolazione agli zeri di Chebychev l’errore commesso ossia
Costruire un vettore contenente gli errori ottenuti per ciascun valore di n e riportare gli errori in un grafico in scala semilogaritmica (semilogy(n,E)).