Calcolo Numerico e Laboratorio di Calcolo
Corso di laurea in Ingegneria Chimica e dei Materiali
Laboratorio 2 MAGGIO 2005
 Esercizio 1
Esercizio 1
- Con riferimento al programma potenziale.f (esercizio 2 del laboratorio del
28 aprile 2005, si recuperi, si compili e si esegua (sempre con i valori
1.56 per r e 10 per Z), il programma
potenziale1.f che risolve lo stesso problema, utilizzando, per il calcolo
del potenziale stesso, una FUNCTION Fortran di nome fun_phi (i risultati su video sono:
potenziale1.out)
Si noti, in tale programma, che le FUNCTION Fortran vengono utilizzate come le Function
intrinseche del Fortran, che le costanti PARAMETER, essendo necessarie solo nel calcolo della
Function, sono state inserite nel modulo Function, e non nel programma principale e che l'istruzione
IMPLICIT NONE deve essere ripetuta anche nel modulo Function. Si noti
anche che il nome dato alla Function, deve essere dichiarato, non solo nell'istruzione di
definizione del modulo, ma anche nel programma principale.
-
Si modifichi potenziale1.f in modo che il valore di Pigreco venga calcolato ed
assegnato ad una variabile PI (sapendo che Pigreco=arcos(-1)).
 Esercizio 2
Esercizio 2
- Si scriva un algoritmo e poi un programma per visualizzare i primi 20
numeri della sequenza di Fibonacci per la quale ogni numero è
la somma dei due numeri precedenti. Inizia con
1, 1, 2, 3, 5, 8, 13, ...
 Esercizio 3
Esercizio 3
- Si scriva un algoritmo che legga in ingresso una coppia di numeri reali
x ed y e ne stampi la somma x+y e la differenza x-y.
- Si scrivano poi, utilizzando un editor a piacere, due programmi Fortran
77: il primo, di nome sem.f, utilizzando per i numeri reali
la semplice precisione (REAL*4) ed il secondo, di nome dop.f,
la doppia precisione (REAL*8)
- Ottenuti i programmi eseguibili funzionanti, si provino gli stessi
sulle seguenti coppie di numeri reali (memorizzate su di un file e lette dal programma
direttamente da tale file) e si confrontino i risultati ottenuti
con quelli della tabella a pagina 31 del testo.
123456789.0
|
123456788.0
|
123456789.0
|
123456790.0
|
0.56543451e6
|
0.21554623e-4
|
1.0
|
0.5e-6
|
0.5654328749876
|
0.5654328510104
|
0.3333333333
|
0.1111111111
|
 Esercizio 4
Esercizio 4
- Si scriva un programma che legga dal file esterno ingresso.dat
le coppie di numeri assegnate nell'esercizio 3 del laboratorio del 28 aprile 2005.
- Il programma calcoli, per ogni coppia di numeri (x,y) i valori
erra=abs(x-y) ed err= abs(x-y)/abs(y), e produca in uscita
un file di nome erra.dat costituito da due colonne di numeri: la prima
contenente il numero della riga, la seconda contenente il valore calcolato
erra. Si produca anche un secondo file err.dat costituito
da due colonne di numeri: la prima contenente il numero della riga, la seconda
contenente il valore calcolato err.
- Si utilizzi il software GNUPLOT per produrre un unico grafico che contenga
due curve: la prima corrispondente ai valori di erra e la seconda
corrispondente ai valori di err.
- Si visualizzi con il software KGHOSTVIEW il file contenente il disegno
e lo si stampi
Soluzione:
figura.ps
 Esercizio 5
Esercizio 5
- Si recuperi il programma
seno.f che calcola il seno goniometrico e della sua derivata
approssimata (variabile dsx) in un intervallo di estremi minx e maxx, con ampiezza dei
sottointervalli h, letta da tastiera.
Lo si compili e lo si faccia eseguire con i valori (di h) 0.5, 0.125, 0.05, 0.001.
- Prendendo spunto dall'esercizio 1, si modifichi tale programma in modo che
il calcolo della derivata approssimata venga effettuato tramite la definizione
di una Function Fortran di nome dersin (in doppia precisione).
-
Si ripetano le esperienze numeriche con gli stessi valori precedentemente utilizzati
(i risultati ottenuti devono essere gli stessi!)
 Esercizio 6
Esercizio 6
- Si scriva un algoritmo per la determinazione delle soluzioni reali
di un'equazione di secondo grado
a*x**2 + b*x + c = 0
a coefficienti reali,
operando tutti
i controlli necessari per determinare se l'equazione ha
radici reali distinte, radici reali coincidenti o nessuna radice reale.
Soluzione: Si vedano gli algoritmi
versione normale e
versione stabile
- Si testi a mano se l'algoritmo restituisce i risultati corretti (nel caso delle radici
complesse, l'algoritmo deve stampare un avviso), scegliendo
opportunamente i valori di ingresso in modo da controllere tutte le possibilità.
- Si traduca poi l'algoritmo
in un programma in Fortran (doppia precisione) e lo si provi nuovamente con i dati
utilizzati per la traccia manuale e con altri dati.
 Esercizio 7
Esercizio 7
Si devono risolvere un certo numero di equazioni di secondo grado,
i cui coefficienti 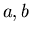 e
e 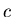 sono:
sono:
Tali terne devono essere memorizzate in un file di nome coeff.dat
aggiungendo un'ultima riga (che servirà da valore di segnalazione per
il programma) contenente
Si scriva un programma che legga riga per riga il file coeff.dat
e che, utilizzando i coefficienti della riga, risolva la corrispondente equazione
di secondo grado (con la versione normale oppure stabile).
I risultati devono essere scritti in un file di nome risultati.dat,
indicando i valori dei tre coefficienti, la scritta indicatrice del tipo di
soluzioni ottenute ed (in caso ve ne siano) anche i valori.
Una possibile uscita su file (per le terne assegnate) dovrebbe contenere
** Coefficienti: a = 1. b = 2. c = 3.
Nessuna soluzione reale
** Coefficienti: a = 3. b = 8. c = 2.
Due soluzioni distinte (x1 <> x2)
-2.38742589 -0.27924078
** Coefficienti: a = 2. b = 4. c = 2.
Due soluzioni coincidenti (x1 = x2)
-1.
** Coefficienti: a = 0. b = 1. c = 2.
Equazione di grado 1 (unica soluzione x1)
-2.
** Coefficienti: a = 3. b = 5. c = 0.
Due soluzioni distinte (x1 <> x2)
-1.66666667 0.
** Coefficienti: a = 4. b = 0. c = 3.
Nessuna soluzione reale
** Coefficienti: a = 4. b = 0. c = -3.
Due soluzioni distinte (x1 <> x2)
-0.866025404 0.866025404
** Coefficienti: a = 0. b = 0. c = 2.
Equazione impossibile
** Coefficienti: a = 3. b = 0. c = 0.
Due soluzioni coincidenti (x1 = x2)
0.
** Coefficienti: a = 0. b = 0. c = 0.
Equazione indeterminata
Soluzioni:
coeff.dat, risultati.dat

 Esercizio 1
Esercizio 1