Calcolo Numerico
Corso di laurea in Ingegneria Meccanica

Laboratorio 14 GIUGNO 2005

Esercizio 1

Si consideri la function Matlab pollag.m che implementa il calcolo del polinomio interpolatore con la formula di Lagrange e lo script di esempio di utilizzo (molto semplice e da completare) mainp.m.
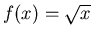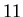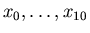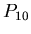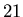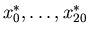Considerata la funzione $f(x)= \sqrt{x}$ , scelti nodi $x_0,\ldots,x_{10}$ equispaziati nell'intervallo lo script valuta il polinomio interpolatore $P_{10}$ in punti equispaziati $x_0^*,\ldots,x_{20}^*$ dello stesso intervallo. In entrambi i casi si è preso come punto iniziale l'estremo sinistro dell'intervallo e come punto finale l'estremo destro dell'intervallo. Si disegna poi sullo stesso grafico, nell'intervallo , la spezzata congiungente i punti dati e quella dei punti interpolati determinati dalla formula di Lagrange.

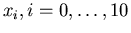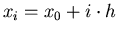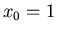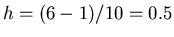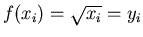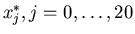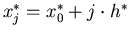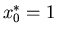Traccia della soluzione: I punti $x_i, i=0,\ldots,10$ sono calcolati come $x_i=x_0+i \cdot h$ , con ed e per essi si valuta $f(x_i)=\sqrt{x_i}=y_i$ . I punti $x_j^*, j=0,\ldots,20$ sono calcolati come $x_j^*=x_0^*+j \cdot h^*$ , con ed 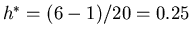. L'algoritmo fornisce i valori 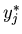. Nell'intervallo assegnato le due spezzate praticamente coincidono.

Esercizio 2

Si consideri la funzione

$\begin{displaymath}f(x) = e^{x}/x^5,\end{displaymath}$

nell'intervallo .
Prendendo spunto dalla function precedente, si costruisca una function, di nome polait.m che valuti il polinomio di interpolazione con lo schema di Neville Aitken (si veda l'algoritmo nevait).
Si scelgano nodi equispaziati di tale intervallo $x_i, i=0,\ldots, 5$ (con e $x_{5}=15$ ) e si calcolino i corrispondenti valori $y_i=f(x_i), i=0,\ldots, 5$ . Si scrivano su di un file di nome nodi.dat le coppie di valori $x_i,y_i, i=0,\ldots,5$ così determinate.
Si scelgano poi nodi equispaziati di tale intervallo $x_i^*, i=0,\ldots, 50$ (con e $x_{50}^*=15$ ) e si calcolino per interpolazione, con l'algoritmo di Neville-Aitken ed utilizzando come nodi i valori $x_i,y_i, i=0,\ldots,5$ , i valori approssimati $y_i^*=P_{5}(x^*_i), i = 0, \ldots, 50$ . Si scrivano su di un file di nome interp.dat le coppie di valori $x_i^*,y_i^*, i=0,\ldots,50$ così determinate.
Si produca un grafico dis.ps che rappresenti, nell'intervallo la curva ottenuta congiungendo i punti $x_i^*,y_i^*, i=0,\ldots,50$ e la curva analitica .

Soluzioni:

nodi.dat, interp.dat

dis.ps

Esercizio 3

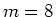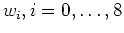Siano date le seguenti 9 coppie di valori (), ed i pesi $w_i, i=0,\ldots, 8$ tutti uguali ad 1, che devono essere letti da un file di nome coppie.dat

$\begin{displaymath} \begin{array}{c\vert\vert r\vert r\vert r\vert r\vert r\vert... ....0308& 1.068& 1.118 & 1.1792 & 1.25& 1.3288& 1.4142 \end{array}\end{displaymath}$

Utilizzando tali valori, si vuole calcolare la retta di regressione .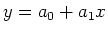
Si costruisca il corrispondente sistema delle equazioni normali 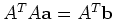$A^TA {\mathbf{a}}= A^T{\mathbf{b}}$ e si scrivano, sul file di nome sistema.dat, la matrice 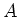, il vettore 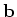${\mathbf{b}}$ , la matrice 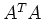ed il vettore 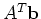$A^T{\mathbf{b}}$ (massimo 4 cifre decimali dopo il punto di radice).
Si risolva tale sistema (con un qualsiasi metodo diretto o con la formula dirett a) e si determini la soluzione 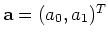${\mathbf{a}}=(a_0,a_1)^T$ , scrivendola poi nel file di nome retta.dat (massimo 4 cifre decimali dopo il punto di radice).
Si rappresentino graficamente i risultati ottenuti producendo la figura regre.ps che deve contenere la retta ed i punti della tabulazione.

Soluzioni:

coppie.dat, sistema.dat

retta.dat

e regre.ps