How to catch a lion in Sahara desert
Mathematical Methods
The Hilbert, or Axiomatic, Method
We place a locked cage at a given point of the desert. We then introduce the following logical system.
- Axiom I. The class of lions in the Sahara Desert is non-void.
- Axiom II. If there is a lion in the Sahara Desert, there is a lion in the cage.
- Rule of Procedure. If p is a theorem, and «p implies q» is a theorem, then q is a theorem.
- Theorem I. There is a lion in the cage.
The Method of Inversive Geometry
We place a spherical cage in the desert, enter it, and lock it. We perform an inversion with respect to the cage. The lion is then in the interior of the cage, and we are outside.
The Method of Projective Geometry
Without loss of generality, we may regard the Sahara Desert as a plane. Project the plane into a line, and then project the line into an interior point of the cage. The lion is projected into the same point.
The Bolzano-Weierstrass Method
Bisect the desert by a line running N-S. The lion is either in the E portion or in the W portion; let us suppose him to be in the W portion. Bisect this portion by a line running E-W. The lion is either in the N portion or in the S portion; let us suppose him to be in the N portion. We continue this process indefinitely, constructing a sufficiently strong fence about the chosen portion at each step. The diameter of the chosen portions approaches zero, so that the lion is ultimately surrounded by a fence of arbitrarily small perimeter.
The "Mengentheoretisch" Method
We observe that the desert is a separable space. It therefore contains an enumerable dense set of points, from which can be extracted a sequence having the lion as limit. We then approach the lion stealthily along this sequence, bearing with us suitable equipment.
The Peano Method
Construct, by standard methods, a continuous curve passing through every point of the desert. It has been remarked that it is possible to traverse such a curve in an arbitrarily short time. Armed with a spear, we traverse the curve in a time shorter than that in which a lion can move his own length.
A Topological Method
We observe that a lion has at least the connectivity of the torus. We transport the desert into four-space. It is then possible
* to carry out such a deformation that the lion can be returned to three-space in a knotted condition. He is then helpless.
The Cauchy, or Functiontheoretical, Method
We consider an analytic lion-valued function
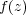
. Let
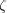
be the cage. Consider the integral
where
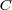
is the boundary of the desert; its value is
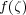
,i.e., a lion in the cage.
†The Wiener Tauberian Method
We procure a tame lion,
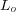
, of class
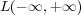
, whose Fourier transform nowhere vanishes, and release it in the desert.
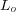
then converges to our cage. By Wiener's General Tauberian Theorem
‡, any other lion,
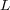
(say), will then converge to the same cage. Alternatively, we can approximate arbitrarily closely to
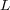
by translating
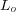
about the desert.
§A Cathegory Method
Let
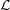
denote the category whose objects are lions, with «ancestor» as the only nontrivial morphism. Let
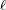
be the category of caged lions. The subcategory
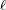
is clearly complete, is nonempty (by inspection), and has both a generator and cogenerator
×. Let
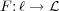
be the forgetful functor, which forgets the cage. By the Adjoint Functor Theorem
Þ the functor F has a coadjoint
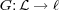
, which reflects each lion into a cage.
Methods from Theoretical Physics
The Dirac Method
We observe that wild lions are, ipso facto, not observable in the Sahara Desert. Consequently, if there are any lions in the Sahara, they are tame. The capture of a tame lion may be left as an exercise for the reader.
The Schrödinger Method
At any given moment there is a positive probability that there is a lion in the cage. Sit down and wait.
The Method of Nuclear Physics
Place a tame lion in the cage, and apply a Majorana exchange operator
|| between it and a wild lion.
As a variant, let us suppose, to fix ideas, that we require a male lion. We place a tame lioness in the cage, and apply a Heisenberg exchange operator
¶ which exchanges the spins.
The Relativistic Method
We distribute about the desert lion bait containing large portions of the Companion of Sirius. When enough bait has been taken, we project a beam of light across the desert. This will bend right round the lion, who will then become so dizzy that he can be approached with impunity.
Methods from Experimental Physics
The Thermodynamical Method
We construct a semi-permeable membrane, permeable to everything except lions, and sweep it across the desert.
The Atom-Splitting Method
We irradiate the desert with slow neutrons. The lion becomes radioactive, and a process of disintegration sets in. When the decay has proceeded sufficiently far, he will become incapable of showing fight.
The Magneto-Optical Method
We plant a large lenticular bed of catnip (Nepeta cataria), whose axis lies along the direction of the horizontal component of the earth's magnetic field, and place a cage at one of its foci. We distribute over the desert large quantities of magnetized spinach (Spinacia oleracea), which, as is well known, has a high ferric content. The spinach is eaten by the herbivorous denizens of the desert, which are in turn eaten by lions. The lions are then oriented parallel to the earth's magnetic field, and the resulting beam of lions is focussed by the catnip upon the cage.
Notes
- * H. Seifert and W. Threlfall, Lehrbuch der Topologie, 1934, pp. 2-3.
- † N.B. By Picard's Theorem (W. F. Osgood, Lehrbuch der Funktionentheorie, vol. 1, 1928, p. 748), we can catch every lion with at most one exception.
- ‡ N. Wiener, The Fourier Integral and Certain of its Applications, 1933, pp. 73-74.
- § N. Wiener, 1. c., p. 89.
- || See, for example, H. A. Bethe and R. F. Bacher, Reviews of Modern Physics, vol. 8, 1936, pp. 82-229; especially pp. 106-107.
- ¶ Ibid.
- × Moses, The Book of Genesis, vii, 15-16.
- Þ P. Freyd, Abelian categories, New York, 1964, pp. 80-91.
Essential Bibliography
- H. Petard, A Contribution to the Mathematical Theory of Big Game Hunting, The American Mathematical Monthly, Vol. 45, No. 7. (Aug. - Sep., 1938), pp. 446-447.
- C. Roselius, On a Theorem of H. Petard, The American Mathematical Monthly, Vol. 74, No. 7. (Aug. - Sep., 1967), pp. 838-839.
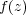 . Let
. Let 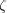 be the cage. Consider the integral
be the cage. Consider the integral 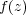 . Let
. Let 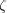 be the cage. Consider the integral
be the cage. Consider the integral 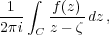
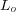 , of class
, of class 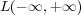 , whose Fourier transform nowhere vanishes, and release it in the desert.
, whose Fourier transform nowhere vanishes, and release it in the desert. 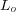 then converges to our cage. By Wiener's General Tauberian Theorem ‡, any other lion,
then converges to our cage. By Wiener's General Tauberian Theorem ‡, any other lion, 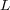 (say), will then converge to the same cage. Alternatively, we can approximate arbitrarily closely to
(say), will then converge to the same cage. Alternatively, we can approximate arbitrarily closely to 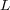 by translating
by translating 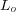 about the desert. §
about the desert. §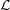 denote the category whose objects are lions, with «ancestor» as the only nontrivial morphism. Let
denote the category whose objects are lions, with «ancestor» as the only nontrivial morphism. Let 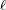 be the category of caged lions. The subcategory
be the category of caged lions. The subcategory 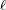 is clearly complete, is nonempty (by inspection), and has both a generator and cogenerator ×. Let
is clearly complete, is nonempty (by inspection), and has both a generator and cogenerator ×. Let 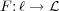 be the forgetful functor, which forgets the cage. By the Adjoint Functor Theorem Þ the functor F has a coadjoint
be the forgetful functor, which forgets the cage. By the Adjoint Functor Theorem Þ the functor F has a coadjoint 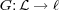 , which reflects each lion into a cage.
, which reflects each lion into a cage.