2 Cyclomatic Complexity

Cyclomatic complexity [MCCABE1] measures the amount of decision logic in a single software module. It is used for two related purposes in the structured testing methodology. First, it gives the number of recommended tests for software. Second, it is used during all phases of the software lifecycle, beginning with design, to keep software reliable, testable, and manageable. Cyclomatic complexity is based entirely on the structure of software's control flow graph.

2.1 Control flow graphs

Each possible execution path of a software module has a corresponding path from the entry to the exit node of the module's control flow graph. This correspondence is the foundation for the structured testing methodology.

As an example, consider the C function in Figure 2-1, which implements Euclid's algorithm for finding greatest common divisors. The nodes are numbered A0 through A13. The control flow graph is shown in Figure 2-2, in which each node is numbered 0 through 13 and edges are shown by lines connecting the nodes. Node 1 thus represents the decision of the "if" statement with the true outcome at node 2 and the false outcome at the collection node 5. The decision of the "while" loop is represented by node 7, and the upward flow of control to the next iteration is shown by the dashed line from node 10 to node 7. Figure 2-3 shows the path resulting when the module is executed with parameters 4 and 2, as in "euclid(4,2)." Execution begins at node 0, the beginning of the module, and proceeds to node 1, the decision node for the "if" statement. Since the test at node 1 is false, execution transfers directly to node 5, the collection node of the "if" statement, and proceeds to node 6. At node 6, the value of "r" is calculated to be 0, and execution proceeds to node 7, the decision node for the "while" statement. Since the test at node 7 is false, execution transfers out of the loop directly to node 11, then proceeds to node 12, returning the result of 2. The actual return is modeled by execution proceeding to node 13, the module exit node.

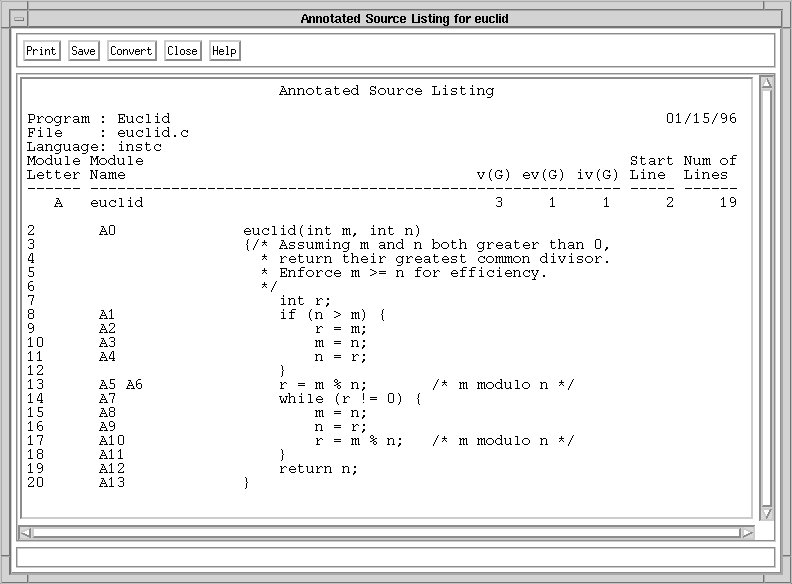
Figure 2-1. Annotated source listing for module "euclid."

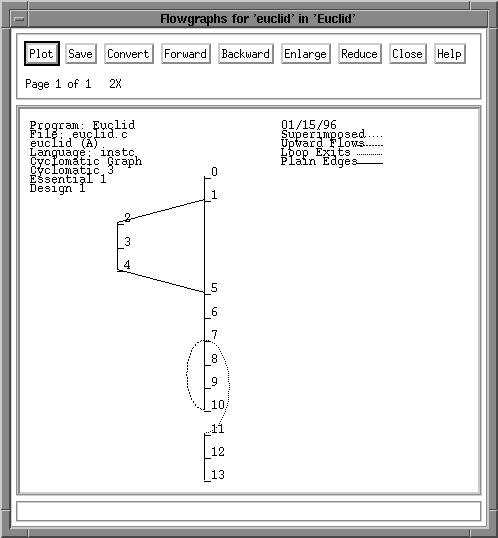
Figure 2-2. Control flow graph for module "euclid."

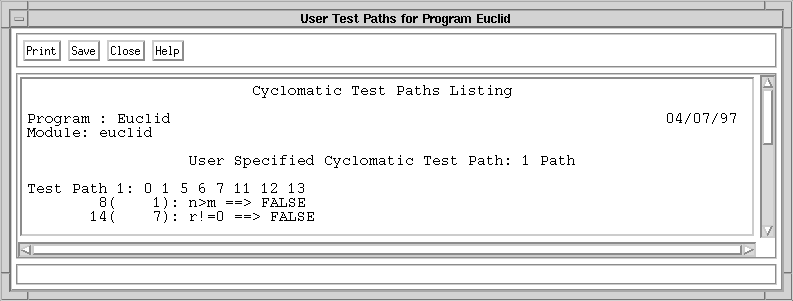
Figure 2-3. A test path through module "euclid."

2.2 Definition of cyclomatic complexity, v(G)

The word "cyclomatic" comes from the number of fundamental (or basic) cycles in connected, undirected graphs [BERGE]. More importantly, it also gives the number of independent paths through strongly connected directed graphs. A strongly connected graph is one in which each node can be reached from any other node by following directed edges in the graph. The cyclomatic number in graph theory is defined as e - n + 1. Program control flow graphs are not strongly connected, but they become strongly connected when a "virtual edge" is added connecting the exit node to the entry node. The cyclomatic complexity definition for program control flow graphs is derived from the cyclomatic number formula by simply adding one to represent the contribution of the virtual edge. This definition makes the cyclomatic complexity equal the number of independent paths through the standard control flow graph model, and avoids explicit mention of the virtual edge.

Figure 2-4 shows the control flow graph of Figure 2-2 with the virtual edge added as a dashed line. This virtual edge is not just a mathematical convenience. Intuitively, it represents the control flow through the rest of the program in which the module is used. It is possible to calculate the amount of (virtual) control flow through the virtual edge by using the conservation of flow equations at the entry and exit nodes, showing it to be the number of times that the module has been executed. For any individual path through the module, this amount of flow is exactly one. Although the virtual edge will not be mentioned again in this document, note that since its flow can be calculated as a linear combination of the flow through the real edges, its presence or absence makes no difference in determining the number of linearly independent paths through the module.

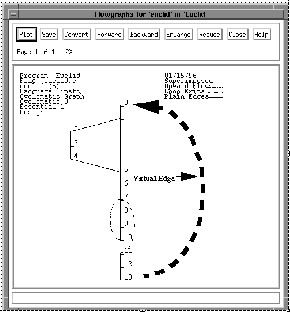
Figure 2-4. Control flow graph with virtual edge.

2.3 Characterization of v(G) using a basis set of control flow paths

Each path has an associated row vector, with the elements corresponding to edges in the flow graph. The value of each element is the number of times the edge is traversed by the path. Consider the path described in Figure 2-3 through the graph in Figure 2-2. Since there are 15 edges in the graph, the vector has 15 elements. Seven of the edges are traversed exactly once as part of the path, so those elements have value 1. The other eight edges were not traversed as part of the path, so they have value 0.

Considering a set of several paths gives a matrix in which the columns correspond to edges and the rows correspond to paths. From linear algebra, it is known that each matrix has a unique rank (number of linearly independent rows) that is less than or equal to the number of columns. This means that no matter how many of the (potentially infinite) number of possible paths are added to the matrix, the rank can never exceed the number of edges in the graph. In fact, the maximum value of this rank is exactly the cyclomatic complexity of the graph. A minimal set of vectors (paths) with maximum rank is known as a basis, and a basis can also be described as a linearly independent set of vectors that generate all vectors in the space by linear combination. This means that the cyclomatic complexity is the number of paths in any independent set of paths that generate all possible paths by linear combination.

Given any set of paths, it is possible to determine the rank by doing Gaussian Elimination on the associated matrix. The rank is the number of non-zero rows once elimination is complete. If no rows are driven to zero during elimination, the original paths are linearly independent. If the rank equals the cyclomatic complexity, the original set of paths generate all paths by linear combination. If both conditions hold, the original set of paths are a basis for the flow graph.

There are a few important points to note about the linear algebra of control flow paths. First, although every path has a corresponding vector, not every vector has a corresponding path. This is obvious, for example, for a vector that has a zero value for all elements corresponding to edges out of the module entry node but has a nonzero value for any other element cannot correspond to any path. Slightly less obvious, but also true, is that linear combinations of vectors that correspond to actual paths may be vectors that do not correspond to actual paths. This follows from the non-obvious fact (shown in section 6) that it is always possible to construct a basis consisting of vectors that correspond to actual paths, so any vector can be generated from vectors corresponding to actual paths. This means that one can not just find a basis set of vectors by algebraic methods and expect them to correspond to paths-one must use a path-oriented technique such as that of section 6 to get a basis set of paths. Finally, there are a potentially infinite number of basis sets of paths for a given module. Each basis set has the same number of paths in it (the cyclomatic complexity), but there is no limit to the number of different sets of basis paths. For example, it is possible to start with any path and construct a basis that contains it, as shown in section 6.3.

The details of the theory behind cyclomatic complexity are too mathematically complicated to be used directly during software development. However, the good news is that this mathematical insight yields an effective operational testing method in which a concrete basis set of paths is tested: structured testing.

2.4 Example of v(G) and basis paths

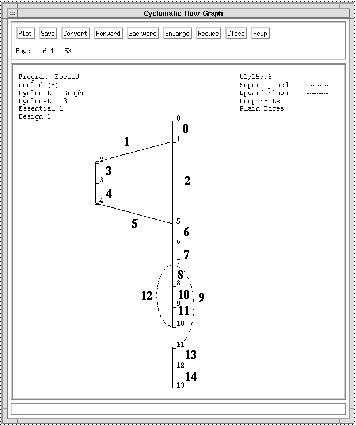
Figure 2-5. Control flow graph with edges numbered.

Module: euclid

			Basis Test Paths: 3 Paths

Test Path B1: 0 1 5 6 7 11 12 13

	8(    1): n>m ==> FALSE

	14(    7): r!=0 ==> FALSE

Test Path B2: 0 1 2 3 4 5 6 7 11 12 13

	8(    1): n>m ==> TRUE

	14(    7): r!=0 ==> FALSE

Test Path B3: 0 1 5 6 7 8 9 10 7 11 12 13

	8(    1): n>m ==> FALSE

	14(    7): r!=0 ==> TRUE

	14(    7): r!=0 ==> FALSE

Any arbitrary path can be expressed as a linear combination of the basis paths B1 through B3. For example, the path P shown in Figure 2-7 is equal to B2 - 2 * B1 + 2 * B3.

Module: euclid

			User Specified Path: 1 Path

Test Path P: 0 1 2 3 4 5 6 7 8 9 10 7 8 9 10 7 11 12 13

	8(    1): n>m ==> TRUE

	14(    7): r!=0 ==> TRUE

	14(    7): r!=0 ==> TRUE

	14(    7): r!=0 ==> FALSE

To see this, examine Figure 2-8, which shows the number of times each edge is executed along each path.

Path/Edge	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
B1	1	0	1	0	0	0	1	1	0	1	0	0	0	1	1
B2	1	1	0	1	1	1	1	1	0	1	0	0	0	1	1
B3	1	0	1	0	0	0	1	1	1	1	1	1	1	1	1
P	1	1	0	1	1	1	1	1	2	1	2	2	2	1	1

Figure 2-8. Matrix of edge incidence for basis paths B1-B3 and other path P.

One interesting property of basis sets is that every edge of a flow graph is traversed by at least one path in every basis set. Put another way, executing a basis set of paths will always cover every control branch in the module. This means that to cover all edges never requires more than the cyclomatic complexity number of paths. However, executing a basis set just to cover all edges is overkill. Covering all edges can usually be accomplished with fewer paths. In this example, paths B2 and B3 cover all edges without path B1. The relationship between basis paths and edge coverage is discussed further in section 5.

Note that apart from forming a basis together, there is nothing special about paths B1 through B3. Path P in combination with any two of the paths B1 through B3 would also form a basis. The fact that there are many sets of basis paths through most programs is important for testing, since it means it is possible to have considerable freedom in selecting a basis set of paths to test.

2.5 Limiting cyclomatic complexity to 10

Somewhat more interesting than the exact complexity limit are the exceptions to that limit. For example, McCabe originally recommended exempting modules consisting of single multiway decision ("switch" or "case") statements from the complexity limit. The multiway decision issue has been interpreted in many ways over the years, sometimes with disastrous results. Some naive developers wondered whether, since multiway decisions qualify for exemption from the complexity limit, the complexity measure should just be altered to ignore them. The result would be that modules containing several multiway decisions would not be identified as overly complex. One developer started reporting a "modified" complexity in which cyclomatic complexity was divided by the number of multiway decision branches. The stated intent of this metric was that multiway decisions would be treated uniformly by having them contribute the average value of each case branch. The actual result was that the developer could take a module with complexity 90 and reduce it to "modified" complexity 10 simply by adding a ten-branch multiway decision statement to it that did nothing.

Consideration of the intent behind complexity limitation can keep standards policy on track. There are two main facets of complexity to consider: the number of tests and everything else (reliability, maintainability, understandability, etc.). Cyclomatic complexity gives the number of tests, which for a multiway decision statement is the number of decision branches. Any attempt to modify the complexity measure to have a smaller value for multiway decisions will result in a number of tests that cannot even exercise each branch, and will hence be inadequate for testing purposes. However, the pure number of tests, while important to measure and control, is not a major factor to consider when limiting complexity. Note that testing effort is much more than just the number of tests, since that is multiplied by the effort to construct each individual test, bringing in the other facet of complexity. It is this correlation of complexity with reliability, maintainability, and understandability that primarily drives the process to limit complexity.

Complexity limitation affects the allocation of code among individual software modules, limiting the amount of code in any one module, and thus tending to create more modules for the same application. Other than complexity limitation, the usual factors to consider when allocating code among modules are the cohesion and coupling principles of structured design: the ideal module performs a single conceptual function, and does so in a self-contained manner without interacting with other modules except to use them as subroutines. Complexity limitation attempts to quantify an "except where doing so would render a module too complex to understand, test, or maintain" clause to the structured design principles. This rationale provides an effective framework for considering exceptions to a given complexity limit.

Rewriting a single multiway decision to cross a module boundary is a clear violation of structured design. Additionally, although a module consisting of a single multiway decision may require many tests, each test should be easy to construct and execute. Each decision branch can be understood and maintained in isolation, so the module is likely to be reliable and maintainable. Therefore, it is reasonable to exempt modules consisting of a single multiway decision statement from a complexity limit. Note that if the branches of the decision statement contain complexity themselves, the rationale and thus the exemption does not automatically apply. However, if all branches have very low complexity code in them, it may well apply. Although constructing "modified" complexity measures is not recommended, considering the maximum complexity of each multiway decision branch is likely to be much more useful than the average. At this point it should be clear that the multiway decision statement exemption is not a bizarre anomaly in the complexity measure but rather the consequence of a reasoning process that seeks a balance between the complexity limit, the principles of structured design, and the fundamental properties of software that the complexity limit is intended to control. This process should serve as a model for assessing proposed violations of the standard complexity limit. For developers with a solid understanding of both the mechanics and the intent of complexity limitation, the most effective policy is: "For each module, either limit cyclomatic complexity to 10 (as discussed earlier, an organization can substitute a similar number), or provide a written explanation of why the limit was exceeded."