


Next: About this document ...
Up: 1esercizi
Previous: 1esercizi
ULTIMO AGGIORNAMENTO: 6. maggio 2005
Convergenza puntuale ed uniforme
Differenza tra convergenza puntuale ed uniforme:
Si supponga di avere una successione di funzioni
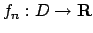 tali che
tali che
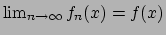 .
Ci chiediamo se il limite è anche uniforme: dovrei avere che
.
Ci chiediamo se il limite è anche uniforme: dovrei avere che
il che è equivalente a dire che (per definizione di limite)
per ogni 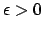 esiste
esiste
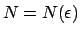 tale che per ogni
tale che per ogni 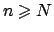 si ha
si ha
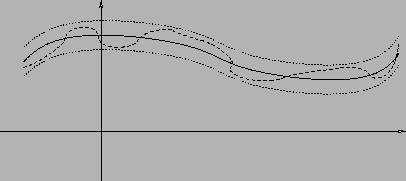
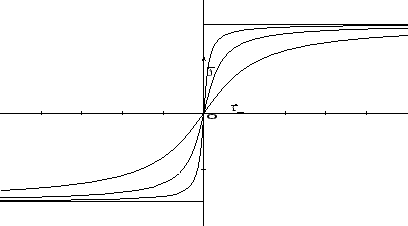
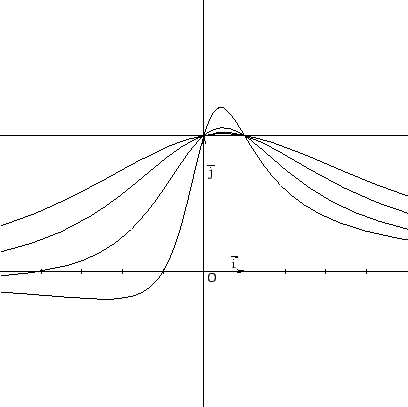
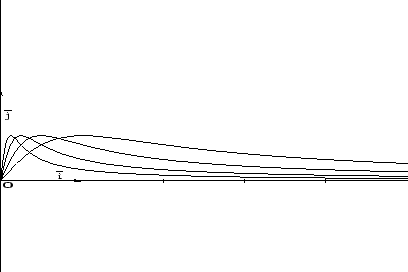
Si veda la Figura 1.1
per avere un'idea dal punto di vista grafico:
la curva in neretto rappresenta il grafico della funzione limite  , i puntini i grafici
di
, i puntini i grafici
di 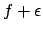 e
e 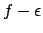 , la curva tratteggiata
il grafico di una possibile
, la curva tratteggiata
il grafico di una possibile  con
con
 .
.
Figura 1.1:
 |
Considerazioni generali:
non esiste un metodo generale (cioè un modo
meccanico che valga in ogni situazione) per studiare la convergenza uniforme.
La prima osservazione che va fatta è che, se
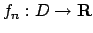 convergono
puntualmente ad
convergono
puntualmente ad  in
in 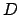 , il candidato ad essere il limite uniforme è
, il candidato ad essere il limite uniforme è  .
La seconda è che
lo studio ha come incognita l'insieme (o gli insiemi) sul quale (o sui
quali)
.
La seconda è che
lo studio ha come incognita l'insieme (o gli insiemi) sul quale (o sui
quali)  converge uniformemente. La domanda da porsi è quindi:
converge uniformemente. La domanda da porsi è quindi:
Chiaramente se 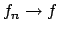 uniformemente su tutto
uniformemente su tutto 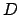 convergerà uniformemente
anche su tutti i sottoinsiemi
convergerà uniformemente
anche su tutti i sottoinsiemi 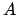 di
di 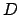 .
.
Un modo per cercare l'estremo superiore di 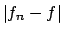 (dove
(dove  è il limite puntuale di
è il limite puntuale di  ) se
) se  e
e  sono di classe
sono di classe 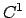 è
di cominciare risolvendo l'equazione
è
di cominciare risolvendo l'equazione
e considerando i punti critici di 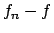 : si faccia attenzione che il minimo, se c'è,
di
: si faccia attenzione che il minimo, se c'è,
di 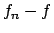 potrebbe essere il massimo di
potrebbe essere il massimo di 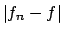 .
Questo però è un modo e comunque non sempre
fornisce l'estremo superiore (ad esempio il sup potrebbe non essere un massimo,
il massimo potrebbe essere assunto agli estremi ecc.).
.
Questo però è un modo e comunque non sempre
fornisce l'estremo superiore (ad esempio il sup potrebbe non essere un massimo,
il massimo potrebbe essere assunto agli estremi ecc.).
In generale
è spesso utile intuire il comportamento della successione di cui bisogna studiare
la convergenza. Un consiglio è quindi quello di studiare qualitativamente, se possibile,
il grafico delle funzioni  .
.

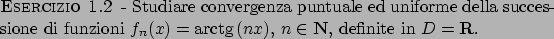

![\begin{esercizio}\rm -\
Studiare convergenza puntuale ed uniforme di $f_n(x) = x(1-x)^n \log n$ in
$[0,1]$.
\end{esercizio}](img25.png)
![\begin{esercizio}\rm -\
Studiare convergenza puntuale ed uniforme di
$f_n: [0,1] \to {\bf R}$, $f_n(x) = {\displaystyle {{nx}\over{1+n^2x^2}}}$.
\end{esercizio}](img26.png)



![\begin{esercizio}\rm -\
Si studi la convergenza puntuale ed uniforme in $[-1, 1]...
...gin{displaymath}
f_n(x) = n \log (1 + x/n) .
\end{displaymath}\end{esercizio}](img30.png)
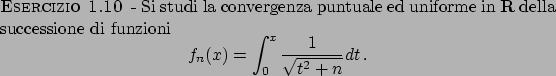
Serie di Funzioni
Una serie di funzioni 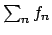 è una speciale successione di funzioni
è una speciale successione di funzioni
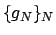 dove
dove
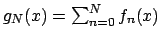 .
.
Ricordo: per le serie di funzioni si ha che
Non ci sono molti criteri in generale per studiare la convergenza uniforme:
in generale, e quindi in particolare
se si ha una serie a termini tutti positivi (o tutti negativi), una strategia possibile
è studiare prima la convergenza totale della serie, ma questo non garantisce di trovare
tutti gli insiemi in cui vi è convergenza uniforme! (si vedano, ad esempio, gli esercizi
1.15 e 1.17), quando si ha
una serie a segni alterni si può sfruttare il criterio di Leibniz.
Per quanto riguarda lo studio della convergenza totale: chiaramente la miglior costante
che controlla su un insieme 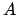 il valore assoluto di
il valore assoluto di 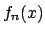 è
è
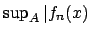 . Quindi per studiare la convergenza totale su
. Quindi per studiare la convergenza totale su 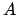 di
di 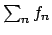 conviene, se si riesce a calcolare l'estremo superiore di
conviene, se si riesce a calcolare l'estremo superiore di 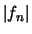 , studiare la serie
, studiare la serie
Non sempre però conviene calcolare l'estremo superiore e ci si può
accontentare di una stima (si veda, ad esempio, la soluzione
dell'ESERCIZIO 1.16)
o non sempre si riesce a calcolare tale estremo superiore
(si veda, ad esempio, la soluzione dell'ESERCIZIO 1.14)



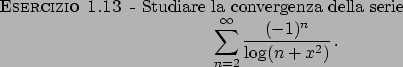



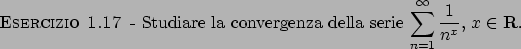
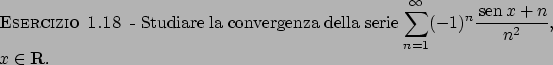
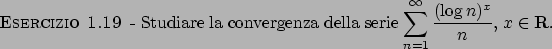
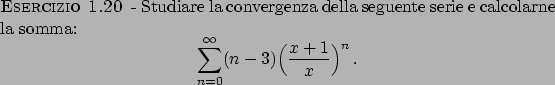
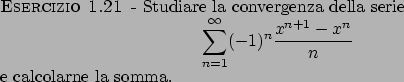

Serie di potenze
Ricordo: le serie di potenze sono particolari serie di funzioni della forma
Il raggio di convergenza di
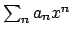 è dato da
è dato da
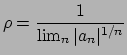 se tale limite esiste
(si vedano le dispense di teoria per la definizione di raggio di convergenza
e l'Esercizio 1.45 per un esempio in cui il limite non
esiste).
se tale limite esiste
(si vedano le dispense di teoria per la definizione di raggio di convergenza
e l'Esercizio 1.45 per un esempio in cui il limite non
esiste).

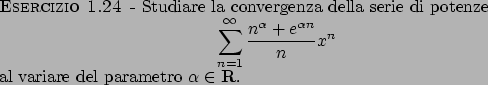
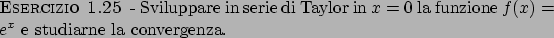

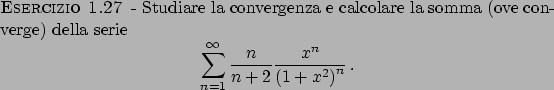
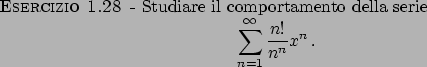
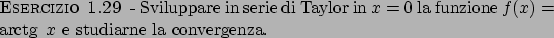
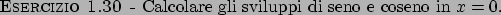
![\begin{esercizio}\rm -\
Studiare la convergenza e calcolare la somma di
\begin{d...
...}\over{n!}} - {{1}\over{(n+1)!}} \Big] x^n .
\end{displaymath}\end{esercizio}](img65.png)
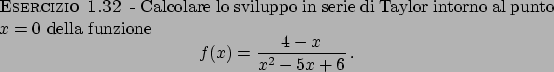
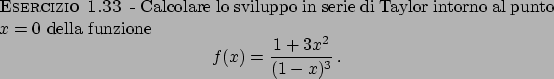




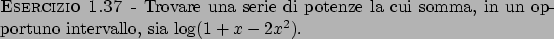


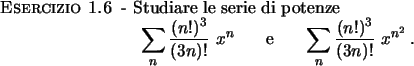

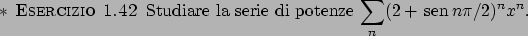
Serie di Fourier
Ricordo: se  è il semiperiodo la serie è data da
è il semiperiodo la serie è data da
dove i coefficienti sono dati da
 )
)
Uguaglianza di Parseval:
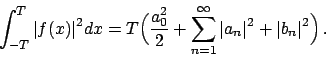 |
(1.1) |
Integrazione della serie di Fourier -
Si supponga di avere  continua a tratti e
continua a tratti e
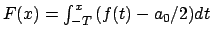 .
Se denotiamo con
.
Se denotiamo con 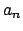 e
e 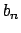 i coefficienti di
i coefficienti di  , con
, con  e
e 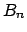 quelli di
quelli di 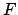 valgono
le relazioni
valgono
le relazioni
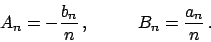 |
(1.2) |
Per quanto riguarda la convergenza della serie (vedi dispense di teoria):
per ogni funzione limitata, continua a tratti e derivabile a tratti la serie
converge puntualmente ovunque (alla media 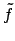 definita nelle dispense di teoria),
uniformemente in ogni intervallo chiuso in cui
definita nelle dispense di teoria),
uniformemente in ogni intervallo chiuso in cui  è continua e totalmente se converge la
serie dei coefficienti
è continua e totalmente se converge la
serie dei coefficienti
visto che
 e
e
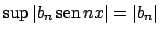 .
.
![\begin{esercizio}\rm -\
Calcolare lo sviluppo di Fourier della funzione $f:[-\pi...
...ella funzione $g:[-\pi,\pi] \to {\bf R}$,
$g(x) = \vert x\vert$.
\end{esercizio}](img93.png)
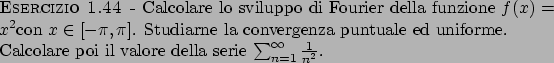

![\begin{esercizio}\rm -\
Calcolare lo sviluppo di Fourier della funzione
\begin{d...
...textrm{se } x \in (0, \pi]
\end{array} \right.
\end{displaymath}\end{esercizio}](img96.png)

Soluzioni
Soluzione 1.1 -
Figura 1.2:
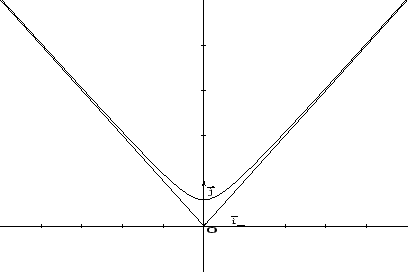 |
Limite puntuale:
Limite uniforme:
Osservazione - Nell'ultimo passaggio si è usata la diseguaglianza
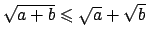 (lasciata per esercizio).
(lasciata per esercizio).
Osservazione - Le funzioni  sono tutte funzioni
sono tutte funzioni 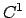 , ma il limite
è solo continuo: la convergenza uniforme si trascina al limite la
continuità, ma non la derivabilità.
, ma il limite
è solo continuo: la convergenza uniforme si trascina al limite la
continuità, ma non la derivabilità.
Soluzione 1.2 -
Il limite puntuale è dato da (si veda la Figura 1.3)
Figura 1.3:
 |
Usiamo il Teorema 1.5 (continuità della funzione limite) delle dispense
che qui ricordiamo brevemente.
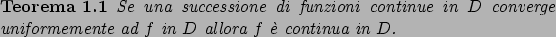
Questo può essere usato anche in negativo: cioè se  è una successione di funzioni continue che converge puntualmente
ad una funzione
è una successione di funzioni continue che converge puntualmente
ad una funzione  non continua, la convergenza non può essere uniforme.
non continua, la convergenza non può essere uniforme.
Concludiamo che se 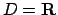
 non converge uniformemente ad
non converge uniformemente ad  .
Ci si può chiedere se ci sono insiemi strettamente contenuti in
.
Ci si può chiedere se ci sono insiemi strettamente contenuti in  sui quali la
convergenza è uniforme.
Si consideri
sui quali la
convergenza è uniforme.
Si consideri
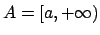 con
con 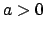 .
La derivata di
.
La derivata di
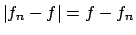 è sempre negativa
(per cui non ci sono punti stazionari).
Questo però ci dice che il massimo è assunto per
è sempre negativa
(per cui non ci sono punti stazionari).
Questo però ci dice che il massimo è assunto per 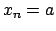 . Per cui
. Per cui
Dalla convergenza puntuale concludiamo che questa quantità converge a zero.
Poiché analogamente si può trattare il caso in cui
![$A = (-\infty, b]$](img113.png) con
con 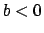 concludiamo che
concludiamo che
 converge uniformemente ad
converge uniformemente ad  su tutti gli insiemi del tipo
su tutti gli insiemi del tipo
![$(-\infty, b] \cup [a, +\infty)$](img115.png) con
con 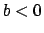 e
e 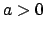 e solo in quelli.
e solo in quelli.
Soluzione 1.3 -
Il limite puntuale è 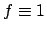 su tutto
su tutto  .
Prima di tutto si osservi che (si vedano alcuni grafici in Figura 1.4)
.
Prima di tutto si osservi che (si vedano alcuni grafici in Figura 1.4)
e anche che
Per ognuna di queste ragioni
e quindi non vi può essere convergenza uniforme su tutto  e nemmeno su semirette.
Vediamo che succede se consideriamo un compatto
e nemmeno su semirette.
Vediamo che succede se consideriamo un compatto
![$[a,b]$](img120.png) .
Calcoliamo la derivata e poniamola uguale a zero. Si ha
.
Calcoliamo la derivata e poniamola uguale a zero. Si ha
che ha come soluzioni
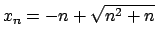 e
e
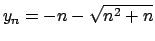 .
Si osservi che
.
Si osservi che 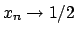 mentre
mentre
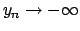 , quindi, qualunque sia
, quindi, qualunque sia
![$[a,b]$](img120.png) ,
, 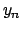 definitivamente non appartiene ad
definitivamente non appartiene ad ![$[a,b]$](img120.png) .
Se
.
Se 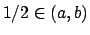 allora
allora 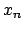 definitivamente appartiene ad
definitivamente appartiene ad ![$[a,b]$](img120.png) .
In
.
In ![$[a,b]$](img120.png) quindi o non ci sono punti stazionari o c'è solamente
quindi o non ci sono punti stazionari o c'è solamente 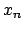 ,
nel quale
,
nel quale  assume il suo valore massimo che vale
assume il suo valore massimo che vale
Attenzione: il massimo di 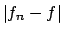 non è detto sia assunto in
non è detto sia assunto in 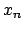 .
Infatti si ha
.
Infatti si ha
che è positiva per 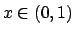 (e negativa altrimenti). Quindi
(e negativa altrimenti). Quindi
Figura 1.4:
 |
Per cui l'estremo superiore (che in realtà è un massimo) è sicuramente
assunto in 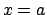 o
o 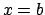 oppure
oppure 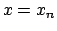 . Per cui
. Per cui
Poiché tutti e tre i valori dell'insieme a destra convergono a zero
si conclude che 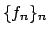 converge uniformemente sui compatti.
converge uniformemente sui compatti.
Soluzione 1.4 -
Convergenza puntuale: 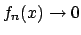 per ogni
per ogni ![$x \in [0,1]$](img139.png) .
Per l'uniforme calcoliamo la derivata di
.
Per l'uniforme calcoliamo la derivata di  :
:
e questa si annulla per 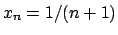 (la funzione è non negativa e nulla agli
estremi,
(la funzione è non negativa e nulla agli
estremi, 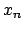 è quindi di massimo). Il valore
è quindi di massimo). Il valore
Soluzione 1.5 -
Il limite puntuale è (in Figura 1.5 sono riportati i grafici di
alcune  )
)
Vediamo se il limite è anche uniforme:
che si annulla per 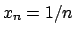 . Ora
. Ora
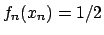 per ogni
per ogni 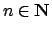 per cui
per cui
Figura 1.5:
 |
Osservazione -
Si osservi che il limite puntuale di funzioni continue può essere continuo
anche se il limite non è uniforme.
Soluzione 1.6 -
Facilmente si ha che
La convergenza non è però uniforme. Infatti
È uniforme però sui limitati. Si consideri, ad esempio, un intervallo
![$[0,a]$](img152.png) con
con 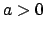 :
:
per cui le funzioni sono crescenti e quindi assumono il massimo in 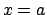 :
:
Calcoliamo l'integrale:
grazie al fatto che 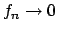 uniformemente in
uniformemente in ![$[0,1]$](img157.png) .
Si noti che anche le funzioni
.
Si noti che anche le funzioni
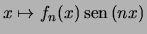 convergono uniformemente a
convergono uniformemente a 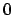 in
in ![$[0,1]$](img157.png) poiché
poiché
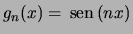 sono equilimitate
(questo è vero solo perché le
sono equilimitate
(questo è vero solo perché le  convergono a zero!
In generale se
convergono a zero!
In generale se  uniformemente e
uniformemente e  sono equilimitate
non possiamo affermare che
sono equilimitate
non possiamo affermare che 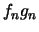 convergono uniformemente).
convergono uniformemente).
Soluzione 1.7 -
Il limite puntuale è 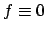 .
Per studiare la convergenza uniforme calcoliamo il massimo delle
.
Per studiare la convergenza uniforme calcoliamo il massimo delle  .
.
Valutiamo il massimo di 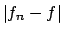 :
:
Si ha che
e quindi vi è convergenza uniforme solo per
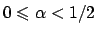 . Calcoliamo l'integrale. Per
. Calcoliamo l'integrale. Per
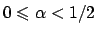
grazie alla convergenza uniforme. Negli altri casi calcolo la primitiva
che è data da
Si ha allora che
Soluzione 1.8 -
Facilmente si vede che
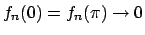 .
.
Se
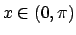 ,
, 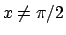 si ha che
si ha che
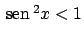 e quindi si ha che esiste
e quindi si ha che esiste  per il quale definitivamente vale
per il quale definitivamente vale
per cui 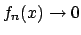 se
se 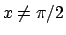 . Se
. Se 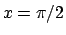 si ha che
si ha che
quindi il limite puntuale è (si veda la Figura 1.6)
Figura 1.6:
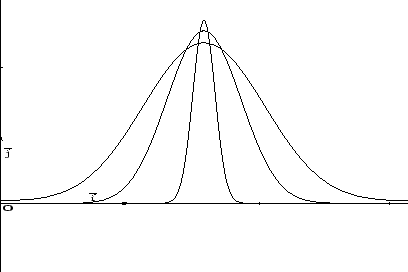 |
Può convergere uniformemente? NO! Perché le
 sono continue e
sono continue e  non lo è.
Vediamo che succede se togliamo un intorno di
non lo è.
Vediamo che succede se togliamo un intorno di 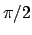 .
Fisso
.
Fisso 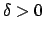 (e minore di
(e minore di 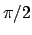 ): in
): in
![$[0, \pi/2 - \delta]$](img183.png)
 è crescente per ogni
è crescente per ogni 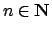 per cui il massimo è assunto
per
per cui il massimo è assunto
per
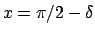 .
Detto
.
Detto 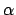 il valore
il valore
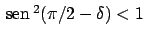 si ha che esiste
si ha che esiste
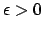 tale che
tale che
e quindi
Allo stesso modo si può procedere in
![$[\pi/2 + \delta, \pi]$](img189.png) . Conclusione:
. Conclusione:
 convergono uniformemente a
convergono uniformemente a 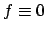 in
tutti gli insiemi del tipo
in
tutti gli insiemi del tipo
![$A_{\delta} = [0, \pi/2 - \delta] \cup [\pi/2 + \delta, \pi]$](img190.png) .
Calcoliamo l'integrale:
.
Calcoliamo l'integrale:
Passando al limite si ha che in 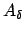 , grazie alla convergenza uniforme,
l'integrale tende a
, grazie alla convergenza uniforme,
l'integrale tende a 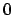 . Concludendo si ha che:
. Concludendo si ha che:
il che significa che l'integrale tende a 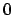 .
.
Soluzione 1.9 -
Proponiamo due svolgimenti. Il primo: scrivendo
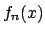 come
come
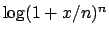 si ottiene che il limite puntuale
è la funzione
si ottiene che il limite puntuale
è la funzione 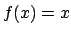 . Vediamo se è uniforme.
Prendiamo in considerazione le funzioni
. Vediamo se è uniforme.
Prendiamo in considerazione le funzioni
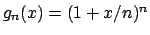 .
Sappiamo dal primo corso di analisi che
.
Sappiamo dal primo corso di analisi che
e converge alla funzione 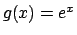 .
Derivando si ottiene
.
Derivando si ottiene
Si osservi però che
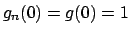 per cui
per cui
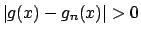 tranne
che per
tranne
che per 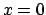 che risulta essere un punto di minimo.
È chiaro che il massimo è assunto quindi per
che risulta essere un punto di minimo.
È chiaro che il massimo è assunto quindi per 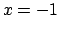 oppure per
oppure per 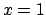 e si ha
e si ha
Per cui 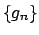 converge uniformemente a
converge uniformemente a 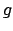 in
in ![$[-1,1]$](img208.png) .
Poiché la funzione
.
Poiché la funzione
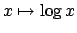 è continua nell'intervallo
è continua nell'intervallo
![$[e^{-1}, e]$](img210.png) (nel quale assumono valori le
(nel quale assumono valori le 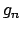 )
e
)
e
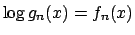 ,
,
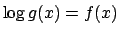 , concludiamo che
anche
, concludiamo che
anche 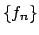 converge uniformemente a
converge uniformemente a  in
in ![$[-1,1]$](img208.png) .
.
Che succede in
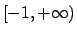 ?
?
Il secondo svolgimento fa uso del seguente risultato (teorema non visto a lezione).
![\begin{teorema}
Sia $(f_n)_n$ una successione in $C^1([a,b])$ tale che
\begin{...
...mente ad una funzione $f$.
Inoltre $f \in C^1([a,b])$ e $f' = g$.
\end{teorema}](img215.png)
Usiamo questo teorema per risolvere l'esercizio.
Calcoliamo direttamente il limite uniforme di
in ![$[-1,1]$](img208.png) . Si ha che
. Si ha che
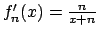 che converge uniformemente
alla costante
che converge uniformemente
alla costante 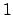 , inoltre
, inoltre 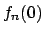 converge a
converge a 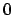 . Per cui
. Per cui  converge
uniformemente alla funzione
converge
uniformemente alla funzione  data da
data da
Soluzione 1.10 -
La successione converge puntualmente alla funzione nulla su tutto  ,
uniformemente solo sui compatti.
,
uniformemente solo sui compatti.
Soluzione 1.11 -
Supponiamo per il momento di dover studiare semplicemente la serie
In un caso del genere ci si può ridurre a studiare la serie geometrica
pensando poi a sostituire a 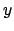
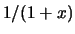 . Sappiamo che la serie geometrica
. Sappiamo che la serie geometrica
Di conseguenza la serie appena scritta converge alla funzione
puntualmente in 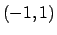 ed uniformemente e totalmente solo
nei compatti
ed uniformemente e totalmente solo
nei compatti
![$[a,b] \subset (-1,1)$](img228.png) . Infatti
. Infatti
e anche
per cui non può esservi convergenza uniforme, e nemmeno totale, in ![$(-1,0]$](img231.png) e in
e in 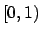 .
Vediamo ora nei compatti
.
Vediamo ora nei compatti
![$[a,b] \subset (-1,1)$](img228.png) .
Infatti: si consideri per semplicità
.
Infatti: si consideri per semplicità ![$[0,b]$](img233.png) con
con 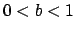 .
Denotiamo con
.
Denotiamo con 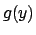 il limite di
il limite di  , cioè
, cioè
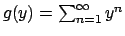 .
Si ha
.
Si ha
Considerando il limite per 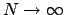 si ottiene la convergenza uniforme.
Analogamente si ottiene in
si ottiene la convergenza uniforme.
Analogamente si ottiene in ![$[a,0]$](img240.png) con
con 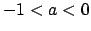 e quindi in ogni
e quindi in ogni
![$[a,b] \subset (-1,1)$](img228.png) .
.
Questo si traduce, per la serie considerata, nella convergenza alla funzione
puntualmente in
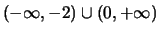 e uniformemente e totalmente
negli insiemi
e uniformemente e totalmente
negli insiemi
![$(-\infty, \alpha]$](img244.png) ,
,
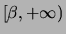 con
con 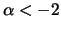 e
e 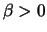 .
Infatti la trasformazione
.
Infatti la trasformazione
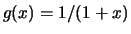 manda l'intervallo
manda l'intervallo ![$[a,0]$](img240.png) ,
con
,
con 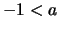 , in
, in
![$(-\infty, {{1-a}\over{a}}]$](img250.png) , e l'intervallo
, e l'intervallo ![$[0,b]$](img233.png) , con
, con 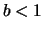 ,
in
,
in
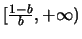 . Se, ad esempio,
. Se, ad esempio,
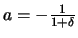 con
con
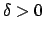 , cioè
, cioè 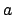 compreso tra
compreso tra 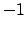 e
e 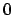 , si ottiene che
, si ottiene che
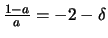 , cioè un numero strettamente minore di
, cioè un numero strettamente minore di 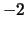 .
Analogamente si vede che
.
Analogamente si vede che
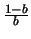 è strettamente positivo.
è strettamente positivo.
Veniamo ora all'esercizio proposto:
poiché la serie data è il limite, per
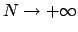 , di
, di
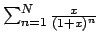 per le somme finite si ha
per le somme finite si ha
Per cui l'insieme di convergenza puntuale contiene sicuramente l'insieme
nel quale converge la serie
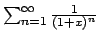 , cioè
, cioè
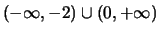 . Si osservi però che la serie data converge
anche per
. Si osservi però che la serie data converge
anche per 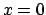 (infatti ogni termine è identicamente nullo!). Perciò l'insieme di
convergenza puntuale è
(infatti ogni termine è identicamente nullo!). Perciò l'insieme di
convergenza puntuale è
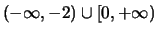 e la funzione limite è
e la funzione limite è
(poiché
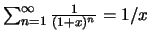 ).
).
Per quanto riguarda le convergenze uniforme e totale
si può ragionare come prima per ottenere che
vi è convergenza negli insiemi del tipo
![$(-\infty, \alpha]$](img244.png) ,
,
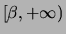 con
con 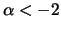 e
e 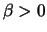 .
Non può esservi convergenza uniforme, e di conseguenza nemmeno totale,
nell'insieme
.
Non può esservi convergenza uniforme, e di conseguenza nemmeno totale,
nell'insieme 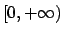 dal momento che la
funzione limite è discontinua in tale insieme mentre le somme parziali sono ovviamente
continue.
dal momento che la
funzione limite è discontinua in tale insieme mentre le somme parziali sono ovviamente
continue.
Cosa succederebbe se invece considerassimo la serie
 ?
?
A questo proposito si veda anche l'ESERCIZIO 1.12.
Soluzione 1.12 -
Per quanto riguarda la serie
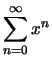 si procede come
nella soluzione dell'ESERCIZIO 1.11 per ottenere la convergenza puntuale
in
si procede come
nella soluzione dell'ESERCIZIO 1.11 per ottenere la convergenza puntuale
in 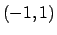 e uniforme e totale nei compatti contenuti in
e uniforme e totale nei compatti contenuti in 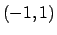 alla funzione
alla funzione
Ciò che può
modificare gli insiemi di convergenza è la presenza di 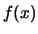 .
L'unica cosa che può alterare il comportamento della serie è il fatto che
.
L'unica cosa che può alterare il comportamento della serie è il fatto che 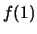 e/o
e/o 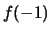 siano
siano 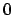 (se
(se 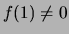 e
e 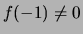 la serie in
la serie in 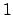 e
e 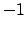 non
converge), escludendo il caso in cui
non
converge), escludendo il caso in cui 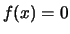 per ogni
per ogni
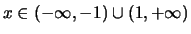 che farebbe banalmente convergere la serie in
tale insieme. Concentriamoci quindi sul comportamento di
che farebbe banalmente convergere la serie in
tale insieme. Concentriamoci quindi sul comportamento di  in
in 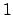 e
e 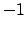 .
Cominciamo considerando
.
Cominciamo considerando
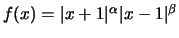 con
con
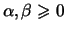 .
Chiaramente la serie converge in
.
Chiaramente la serie converge in 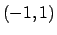 e non converge in
e non converge in
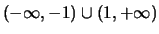 .
Nel punto
.
Nel punto 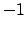 , nel quale la serie
, nel quale la serie 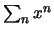 non è determinata, si ha che per qualunque
valore positivo di
non è determinata, si ha che per qualunque
valore positivo di 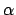
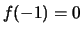 e questo fa sì
che la serie in
e questo fa sì
che la serie in 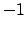 converga. Nel punto
converga. Nel punto 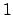 invece affinché la serie converga
bisogna che
invece affinché la serie converga
bisogna che
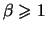 (per
(per 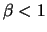 la serie diverge a
la serie diverge a 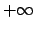 ).
Il limite puntuale è dato dalla funzione
).
Il limite puntuale è dato dalla funzione
Vediamo ora le convergenze uniforme e totale.
Giacché in ![$[-1,0]$](img286.png) vale la seguente stima
vale la seguente stima
possiamo limitarci, per la convergenza totale in ![$[-1,0]$](img286.png) ,
a studiare la funzione
,
a studiare la funzione
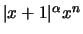 dal momento che,
dalla stima appena sopra, si ha
dal momento che,
dalla stima appena sopra, si ha
Derivando la funzione
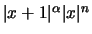 si ottiene il massimo in
si ottiene il massimo in
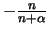 e valutando la funzione in tal punto
si ottiene che il valore massimo (per
e valutando la funzione in tal punto
si ottiene che il valore massimo (per
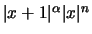 ) è dato da
) è dato da
Poiché
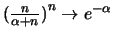 e
e
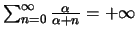 ,
dalla prima delle due disuguaglianze in
,
dalla prima delle due disuguaglianze in 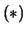 si deduce che la serie non può convergere totalmente in
si deduce che la serie non può convergere totalmente in ![$[-1,0]$](img286.png) .
.
In maniera del tutto analoga si può vedere che
il massimo di
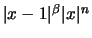 è assunto in
è assunto in
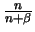 e
vale
e
vale
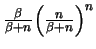 e quindi la serie non converge totalmente
in
e quindi la serie non converge totalmente
in ![$[0,1]$](img157.png) .
Però sui compatti
.
Però sui compatti
![$[a,b] \subset (-1,1)$](img228.png) , dalla convergenza totale
della serie
, dalla convergenza totale
della serie 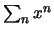 e dalla limitatezza di
e dalla limitatezza di  , vi è convergenza totale.
, vi è convergenza totale.
Veniamo ora alla convergenza uniforme. In ![$[-1,0]$](img286.png) la serie è a segni alterni.
Dal criterio di Leibniz, e usando la seconda disuguaglianza in
la serie è a segni alterni.
Dal criterio di Leibniz, e usando la seconda disuguaglianza in 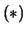 ,
ricaviamo che
,
ricaviamo che
Tale quantità chiaramente tende a zero quando 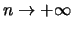 , per cui
la serie converge uniformemente in
, per cui
la serie converge uniformemente in ![$[-1,0]$](img286.png) .
.
In ![$[0,1]$](img157.png) la convergenza uniforme dipende dal valore del parametro
la convergenza uniforme dipende dal valore del parametro  .
Per
.
Per 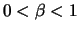 la serie in
la serie in 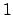 diverge positivamente, per cui non può esservi
convergenza uniforme; per
diverge positivamente, per cui non può esservi
convergenza uniforme; per 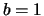 il limite delle somme parziali, tutte continue, è una
funzione discontinua, per cui non può esservi
convergenza uniforme; per
il limite delle somme parziali, tutte continue, è una
funzione discontinua, per cui non può esservi
convergenza uniforme; per  si ha
si ha
Limitandoci a considerare
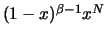 , poiché
, poiché
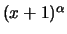 è compreso
tra
è compreso
tra 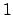 e
e 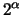 per
per ![$x \in [0,1]$](img139.png) , valutando la derivata si ha
, valutando la derivata si ha
che è il punto di massimo (verificare!), nel quale la funzione assume il valore
che tende a zero (verificare!) per ogni  .
.
Nel caso generale possiamo concludere che se 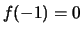 vi è convergenza uniforme
in
vi è convergenza uniforme
in ![$[-1,0]$](img286.png) , nell'intervallo positivo la serie si comporta come
, nell'intervallo positivo la serie si comporta come 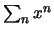 se
se
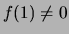 oppure se
oppure se 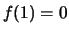 ed esiste
ed esiste
 tale che
tale che
cioè se l'ordine di infinitesimo di  in
in 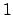 è minore di
è minore di 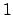 , se
, se
cioè se l'ordine di infinitesimo di  in
in 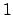 è
è 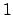 il limite esiste in tutto
il limite esiste in tutto
![$[0,1]$](img157.png) , ma non è continuo, se invece esiste
, ma non è continuo, se invece esiste 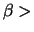 tale che
tale che
cioè se l'ordine di infinitesimo di  in
in 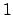 è maggiore di
è maggiore di 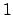 , la serie
converge uniformemente in tutto
, la serie
converge uniformemente in tutto ![$[0,1]$](img157.png) .
Per la totale bisognerà valutare il massimo e fare i conti.
.
Per la totale bisognerà valutare il massimo e fare i conti.
Per quanto riguarda la serie
 , proposta alla fine
della soluzione dell'ESERCIZIO 1.11, si può concludere che
la serie converge uniformemente in
, proposta alla fine
della soluzione dell'ESERCIZIO 1.11, si può concludere che
la serie converge uniformemente in 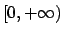 .
.
Soluzione 1.13 -
Converge totalmente su  .
.
Soluzione 1.14 -
Puntuale per ogni 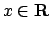 perché, ad esempio,
perché, ad esempio,
In generale vale, per 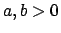 , che
, che
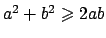 , per cui
, per cui
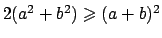 , da cui
, da cui
per cui la serie converge totalmente in  .
.
Soluzione 1.15 -
Per ogni 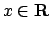
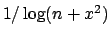 è decrescente in
è decrescente in 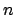 per cui la serie
è convergente per ogni
per cui la serie
è convergente per ogni 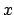 . La stima del resto
. La stima del resto
quindi vi è convergenza uniforme su tutto  . Ovviamente non vi è la
totale: si ha che
. Ovviamente non vi è la
totale: si ha che
(il massimo è assunto per 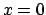 ,
fare la derivata per esercizio!) e la serie
,
fare la derivata per esercizio!) e la serie
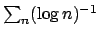 diverge.
Non c'è convergenza totale nemmeno in nessun intervallo
diverge.
Non c'è convergenza totale nemmeno in nessun intervallo 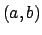 (o
(o ![$[a,b]$](img120.png) )
poiché
)
poiché
Soluzione 1.16 -
Per 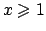 si ha che
si ha che
per cui la serie diverge. Per 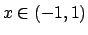 si ha che
si ha che
per cui vi è convergenza assoluta. Per
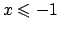
Verifichiamo che è monotona decrescente in 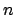 : mi chiedo se
: mi chiedo se
cioè se
il che è equivalente a
che è vero per ogni 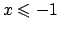 e per ogni
e per ogni 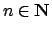 .
Usando il criterio di Leibniz si conclude che la serie converge in
.
Usando il criterio di Leibniz si conclude che la serie converge in
![$(- \infty, -1]$](img339.png) .
.
Quindi converge puntualmente in 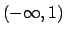 .
.
Dalla stima in 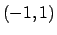 si vede che vi è convergenza totale
in
si vede che vi è convergenza totale
in ![$[0,a]$](img152.png) per ogni
per ogni 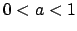 ,
ma non può esservi in
,
ma non può esservi in 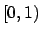 . Infatti
. Infatti
in quanto le funzioni
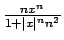 sono continue (anche
in
sono continue (anche
in 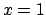 !!), ma la loro
somma su
!!), ma la loro
somma su 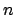 diverge a
diverge a 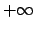 in
in 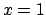 .
Per
.
Per 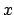 negativo si ha:
negativo si ha:
Conclusione: vi è convergenza puntuale in 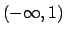 e uniforme e totale
su tutti gli insiemi del tipo
e uniforme e totale
su tutti gli insiemi del tipo ![$(-\infty, a]$](img345.png) con
con 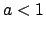 .
.
Soluzione 1.17 -
Questo è un esempio molto semplice si serie di funzioni non negative che converge
uniformemente, ma non totalmente.
La funzione  è a supporto compatto e le
è a supporto compatto e le  non sono altro che traslazioni
di
non sono altro che traslazioni
di  . Di conseguenza
. Di conseguenza 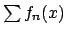 in realtà è una somma finita, per cui
c'è convergenza puntuale (e assoluta, visto che le
in realtà è una somma finita, per cui
c'è convergenza puntuale (e assoluta, visto che le  sono tutte non negative)
su tutto
sono tutte non negative)
su tutto  .
C'è convergenza uniforme? Si, su tutto
.
C'è convergenza uniforme? Si, su tutto  , perché
, perché
C'è convergenza totale? NO! perché il massimo di  è ovviamente
è ovviamente 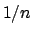 assunto per
assunto per 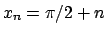 e la serie
e la serie
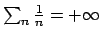 .
Converge, però, totalmente sui sottoinsiemi del tipo
.
Converge, però, totalmente sui sottoinsiemi del tipo ![$(-\infty, a]$](img345.png) .
.
EX: modificare le  in modo tale da avere convergenza totale su
in modo tale da avere convergenza totale su  .
.
Soluzione 1.18 -
Per 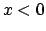
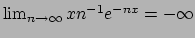 per cui la serie diverge.
Per
per cui la serie diverge.
Per 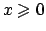 la serie invece converge (per
la serie invece converge (per 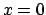 è identicamente nulla,
per
è identicamente nulla,
per 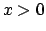 si può usare, ad esempio, il criterio del rapporto).
Vediamo che in
si può usare, ad esempio, il criterio del rapporto).
Vediamo che in 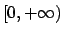 la serie converge totalmente.
Derivando si ottiene che il punto
la serie converge totalmente.
Derivando si ottiene che il punto 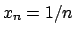 è stazionario. Poiché
è stazionario. Poiché 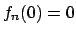 ,
,
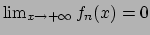 e
e
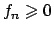
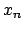 risulta punto di massimo.
Quindi
risulta punto di massimo.
Quindi
Soluzione 1.19 -
Per 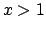 converge e per
converge e per 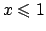 diverge a
diverge a 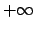 . Poiché la funzione
. Poiché la funzione
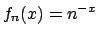 è decrescente si ha che
è decrescente si ha che
e la serie
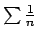 diverge. Idem per la convergenza uniforme:
diverge. Idem per la convergenza uniforme:
Se invece si considera un qualunque insieme del tipo 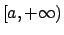 con
con 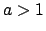 si ha, sempre per il fatto che
si ha, sempre per il fatto che  è decrescente, che
è decrescente, che
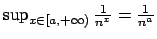 e
e
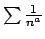 converge per ogni
converge per ogni 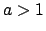 . Concludendo si ha convergenza totale,
e quindi anche uniforme, in tutti gli insiemi del tipo
. Concludendo si ha convergenza totale,
e quindi anche uniforme, in tutti gli insiemi del tipo 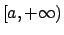 con
con 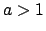 .
.
Soluzione 1.22 -
Posso fare il cambio 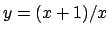 e studiare
e studiare
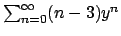 .
Il raggio di convergenza è (si vede facilmente)
.
Il raggio di convergenza è (si vede facilmente) 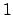 , per cui la serie converge
puntualmente per
, per cui la serie converge
puntualmente per 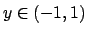 . La convergenza, al solito,
è totale nei compatti
. La convergenza, al solito,
è totale nei compatti
![$[a,b] \subset (-1,1)$](img228.png) , ma non in
, ma non in 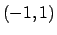 .
Posso scrivere
.
Posso scrivere
e vedere 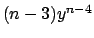 come la derivata di
come la derivata di  . Abbiamo
. Abbiamo
e
Conclusione:
dove la convergenza è puntuale per 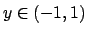 e totale sui compatti
e totale sui compatti
![$[a,b] \subset (-1,1)$](img228.png) . La funzione
. La funzione
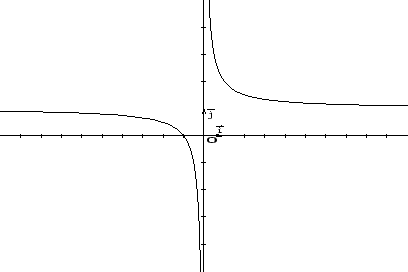
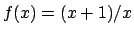 ha il grafico
in Figura 1.7
ha il grafico
in Figura 1.7
Figura 1.7:
 |
per cui, tornando a considerare 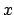 , si ha che
, si ha che
dove la convergenza è puntuale per
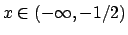 e totale negli insiemi del tipo
e totale negli insiemi del tipo
![$[a,b] \subset (- \infty , -1/2)$](img382.png) . Infatti
. Infatti
Soluzione 1.25 -
Calcolando il seguente limite
si ha che il raggio è 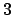 . Conclusione: la serie converge (puntualmente)
in
. Conclusione: la serie converge (puntualmente)
in 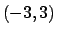 e non converge (puntualmente) in
e non converge (puntualmente) in
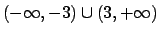 . Vediamo in
. Vediamo in 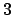 e
e 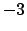 che succede.
che succede.
Conclusione: si ha convergenza puntuale (solo) in 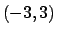 . Vediamo gli altri tipi di
convergenza.
. Vediamo gli altri tipi di
convergenza.
![\begin{teorema}
Una serie di potenze centrata in $0$converge totalmente in ogni intervallo chiuso
del tipo $[-a,a]$ con $a<\rho$.
\end{teorema}](img390.png)
Si ha di conseguenza convergenza totale, e quindi uniforme, in ogni
intervallo ![$[-a,a]$](img391.png) con
con 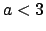 . Vediamo se si ha convergenza uniforme anche in
. Vediamo se si ha convergenza uniforme anche in
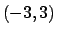 .
Ragionando come al solito (si veda, ad esempio, la risoluzione
dell'esercizio 1.11) si deduce che la serie non può convergere
uniformemente in
.
Ragionando come al solito (si veda, ad esempio, la risoluzione
dell'esercizio 1.11) si deduce che la serie non può convergere
uniformemente in 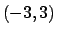 e quindi nemmeno totalmente.
e quindi nemmeno totalmente.
Si osservi che la serie ha come somma la funzione
Soluzione 1.26 -
Si può fare il limite della radice 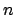 -esima di
-esima di
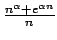 oppure pensare la serie come (perché?)
oppure pensare la serie come (perché?)
e studiare separatamente le due serie. Seguiamo quest'ultima strada.
Il primo termine:
il secondo termine:
Se 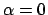 : il raggio è lo stesso e la serie diventa
: il raggio è lo stesso e la serie diventa
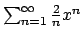 . Vediamo gli estremi:
per
. Vediamo gli estremi:
per 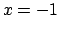 si, per
si, per 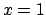 no. Insieme di convergenza puntuale
no. Insieme di convergenza puntuale
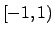 . La convergenza è uniforme? Non può esserlo dappertutto (vedi
esercizio precedente).
. La convergenza è uniforme? Non può esserlo dappertutto (vedi
esercizio precedente).

Sicuramente abbiamo convergenza totale negli insiemi del tipo ![$[a,b]$](img120.png) con
con
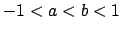 , non abbiamo convergenza uniforme, e quindi nemmeno totale,
in
, non abbiamo convergenza uniforme, e quindi nemmeno totale,
in 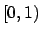 . Vediamo in
. Vediamo in ![$[-1,0]$](img286.png) : qui la serie è a segni alterni, per vedere se
la serie è uniformemente convergente uso il criterio di Leibniz. Detta
: qui la serie è a segni alterni, per vedere se
la serie è uniformemente convergente uso il criterio di Leibniz. Detta
 la somma della serie e
la somma della serie e  le somme parziali devo vedere se vale
le somme parziali devo vedere se vale
cioè
quindi vi è convergenza uniforme in ![$[-1,0]$](img286.png) , ma non totale!
Concludendo: per
, ma non totale!
Concludendo: per 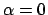 si ha che la serie converge puntualmente
in
si ha che la serie converge puntualmente
in 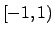 , uniformemente in
, uniformemente in
![$[-1, b] \subset [-1, 1)$](img405.png) e totalmente
in ogni
e totalmente
in ogni
![$[a,b] \subset (-1,1)$](img228.png) .
.
Gli altri casi: se 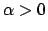 il raggio è
il raggio è  .
Il primo termine sicuramente converge totalmente in
.
Il primo termine sicuramente converge totalmente in
![$[-1/e^{\alpha}, 1/e^{\alpha}]$](img408.png) , quindi limitiamoci a considerare il secondo.
Negli estremi: per
, quindi limitiamoci a considerare il secondo.
Negli estremi: per
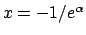 la serie converge, per
la serie converge, per
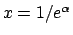 la serie
diverge, infatti si ha rispettivamente
la serie
diverge, infatti si ha rispettivamente
Convergenza uniforme e totale come sopra:
Se 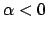 il raggio è
il raggio è 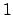 . Vediamo gli estremi: il secondo termine
questa volta converge totalmente in
. Vediamo gli estremi: il secondo termine
questa volta converge totalmente in ![$[-1,1]$](img208.png) . Il primo negli estremi è
. Il primo negli estremi è
che convergono entrambe. Vi è convergenza totale in ![$[-1,1]$](img208.png) .
.
Soluzione 1.27 -
È facile vedere che
Per cui lo sviluppo di Taylor è dato da
Vediamo di studiare la convergenza di questa serie:
puntuale in tutto  , ad esempio con il criterio della radice
, ad esempio con il criterio della radice 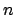 -esima.
Non può essere uniforme in tutto
-esima.
Non può essere uniforme in tutto  perché
perché
Se anche ci limitiamo a
![$x\in (-\infty , 0]$](img418.png) abbiamo
(
abbiamo
(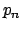 il polinomio di grado
il polinomio di grado 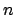 delle somme fino all'
delle somme fino all'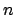 -esimo termine)
-esimo termine)
Vediamo cosa si può dire: se mi limito a considerare un intervallo
![$[a,b]$](img120.png) ho che
ho che
per la crescenza di 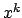 . La serie data dai maggioranti converge. Concludendo:
la serie di Taylor in
. La serie data dai maggioranti converge. Concludendo:
la serie di Taylor in 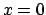 è data da
è data da
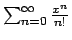 che converge puntualmente su tutto
che converge puntualmente su tutto  e uniformemente e totalmente
solo sui compatti.
e uniformemente e totalmente
solo sui compatti.
Soluzione 1.29 -
La serie dell'esercizio non è una serie di potenze. Tuttavia lo studio di tale
serie può essere ricondotto allo studio di una serie di potenze.
Innanzitutto si osservi che
che è sempre minore di 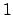 (per esercizio vedere che
(per esercizio vedere che
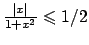 ).
Di conseguenza la serie converge assolutamente per ogni
).
Di conseguenza la serie converge assolutamente per ogni 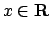 .
Calcoliamo la somma della serie (per
.
Calcoliamo la somma della serie (per 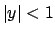 )
)
Si ha che
Ora mi chiedo:
La risposta è si, perché
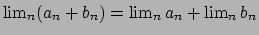 qualora i due limiti a destra (o almeno uno di essi) esistano e nel nostro caso le due
serie a destra convergono entrambe (per
qualora i due limiti a destra (o almeno uno di essi) esistano e nel nostro caso le due
serie a destra convergono entrambe (per 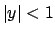 ).
Prendiamo in esame il secondo termine:
).
Prendiamo in esame il secondo termine:
dove l'ultimo passaggio con il punto esclamativo
è lecito se la convergenza è uniforme!! (e lo è se 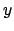 è fissato tra
è fissato tra 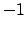 e
e 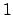 ).
Per integrare
).
Per integrare
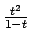 dividiamo
dividiamo 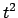 per
per 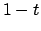 e scriviamo
e scriviamo
e quindi integrando
Tirando le fila si ha
Si osservi che questa funzione è regolare anche se sembra avere singolarità in 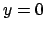 .
Infatti
.
Infatti
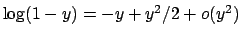 e quindi
e quindi
Tornando al nostro problema: poiché la quantità
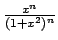 è sempre minore di
è sempre minore di 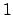 la serie
la serie
converge puntualmente per ogni 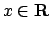 ; converge pure uniformemente
e totalmente su
; converge pure uniformemente
e totalmente su  poiché
poiché
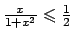 .
Si conclude sostituendo nell'espressione di sopra
.
Si conclude sostituendo nell'espressione di sopra
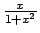 al posto di
al posto di 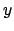
Soluzione 1.30 -
Usiamo una conseguenza del seguente risultato.

Allora calcoliamo il limite della radice 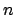 -esima calcolando il rapporto.
(provare a farlo con la radice
-esima calcolando il rapporto.
(provare a farlo con la radice 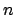 -esima!!!)
-esima!!!)
quindi vi è convergenza puntuale in 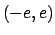 e non vi è
in
e non vi è
in
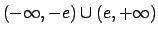 . Vediamo gli estremi:
. Vediamo gli estremi:
per cui
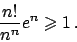 |
(1.3) |
La serie quindi non converge per 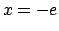 e diverge a
e diverge a 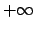 per
per 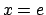 .
Ovviamente converge totalmente e uniformemente in tutti
gli intervalli
.
Ovviamente converge totalmente e uniformemente in tutti
gli intervalli
![$[a,b] \subset (-e, e)$](img454.png) .
Come al solito si ha che la serie non può convergere
uniformemente in
.
Come al solito si ha che la serie non può convergere
uniformemente in 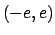 .
.
Anziché la stima (1.3) si può usare, per studiare il comportamento
della serie in 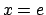 la formula di Stirling
la formula di Stirling
Soluzione 1.31 -
Sappiamo che la serie geometrica
Possiamo allora concludere che la serie
Studiamo questa serie. Converge puntualmente in 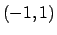 . Per
. Per 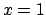 e per
e per 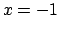 ovviamente non converge. Al solito,
la serie non convergerà uniformemente in
ovviamente non converge. Al solito,
la serie non convergerà uniformemente in 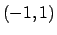 , ma è facile vedere che
converge totalmente in tutti i compatti
, ma è facile vedere che
converge totalmente in tutti i compatti ![$[a,b]$](img120.png) contenuti in
contenuti in 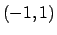 .
Calcoliamo la derivata di
.
Calcoliamo la derivata di
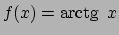
Integrando termine a termine si ha, posto
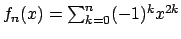 , grazie alla convergenza uniforme
, grazie alla convergenza uniforme
Ora
per cui
per ogni ![$x \in [-1,1]$](img464.png) e la convergenza uniforme solo sui compatti
contenuti in
e la convergenza uniforme solo sui compatti
contenuti in 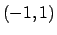 .
.
Soluzione 1.32 -
Calcoliamo la derivata di
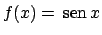 .
.
e poi il ciclo si ripete. Quindi lo sviluppo in 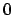 è dato da
è dato da
Vediamo la convergenza. Per il criterio di Leibniz converge per ogni 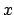 reale.
La convergenza è uniforme e totale solo sui compatti (in modo analogo
all'esercizio precedente). In modo simile si calcola anche lo sviluppo del
coseno
reale.
La convergenza è uniforme e totale solo sui compatti (in modo analogo
all'esercizio precedente). In modo simile si calcola anche lo sviluppo del
coseno
Soluzione 1.33 -
Si ha che
per cui il limite della radice 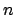 -esima è
-esima è 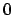 : la serie converge per ogni
: la serie converge per ogni
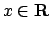 .
Prima di studiare le convergenze uniforme e totale calcoliamo la somma della serie.
Sappiamo che
.
Prima di studiare le convergenze uniforme e totale calcoliamo la somma della serie.
Sappiamo che
Si ha che
per cui, grazie alla convergenza uniforme posso invertire il segno di derivata
con il limite e ottenere
Vediamo la convergenza uniforme in  :
:
quindi non vi è convergenza uniforme in  . Nemmeno se
ci limitiamo a semirette
. Nemmeno se
ci limitiamo a semirette 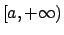 , perché l'estremo superiore è
, perché l'estremo superiore è 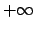 proprio perché consideriamo la semiretta fino a
proprio perché consideriamo la semiretta fino a 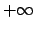 . Che succede
se consideriamo
. Che succede
se consideriamo ![$(-\infty, 0]$](img474.png) ?
?
perché
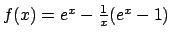 è limitata in
è limitata in ![$(-\infty, 0]$](img474.png) , mentre
un polinomio di grado
, mentre
un polinomio di grado 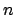 no!
no!
(come, ad esempio, fatto per 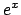 ).
Per
).
Per ![$x \in [-a,a]$](img478.png) con
con 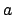 positivo
positivo
La serie
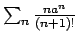 converge per ogni
converge per ogni 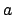 reale
per cui si ha convergenza totale e uniforme in ogni compatto.
reale
per cui si ha convergenza totale e uniforme in ogni compatto.
Soluzione 1.34 -
Spezzando il polinomio 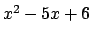 come prodotto di
come prodotto di 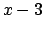 e
e 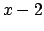 si ottiene che
si ottiene che
Sapendo che, per  , la serie
, la serie
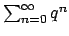 converge al valore
converge al valore
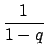 si può scrivere
si può scrivere
che converge per
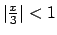 , cioè per
, cioè per 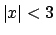 .
L'altro termine:
.
L'altro termine:
che converge per
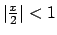 , cioè per
, cioè per 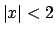 . Sarà possibile effettuare la
somma solo dove convergono entrambe, quindi sicuramente per
. Sarà possibile effettuare la
somma solo dove convergono entrambe, quindi sicuramente per 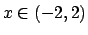 si ha che
si ha che
Soluzione 1.35 -
Si osservi che
Poiché la serie
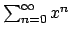 converge uniformemente in ogni intervallo
chiuso
converge uniformemente in ogni intervallo
chiuso
![$[a,b] \subset (-1,1)$](img228.png) e così pure la serie delle sue derivate (prime e seconde, ma
non solo) si può affermare che (per quei valori di
e così pure la serie delle sue derivate (prime e seconde, ma
non solo) si può affermare che (per quei valori di
![$x \in [a,b] \subset (-1,1)$](img498.png) con
con 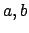 arbitrari, ma
arbitrari, ma 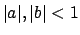 , per cui per ogni
, per cui per ogni 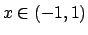 )
)
Per cui dove vi è convergenza per entrambe le serie, e in questo caso
entrambe convergono in 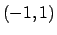 , vale
, vale
Soluzione 1.36 -
La funzione  può essere scritta nei seguenti modi
può essere scritta nei seguenti modi
Perché scartiamo il primo dei due? I due modi non sono equivalenti:
la funzione  è definita quando il suo argomento è positivo, e cioè quando
è definita quando il suo argomento è positivo, e cioè quando
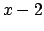 e
e 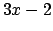 hanno lo stesso segno. Quindi
hanno lo stesso segno. Quindi  può essere spezzata come sopra
nel primo modo se
può essere spezzata come sopra
nel primo modo se 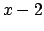 e
e 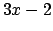 sono entrambi positivi, nel secondo modo
se
sono entrambi positivi, nel secondo modo
se 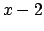 e
e 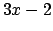 sono entrambi negativi. Per
sono entrambi negativi. Per 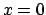 , intorno al quale vogliamo
sviluppare
, intorno al quale vogliamo
sviluppare  , le funzioni
, le funzioni
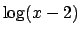 ,
, 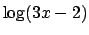 non sono definite, mentre
non sono definite, mentre
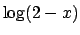 e
e 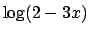 si.
si.
Per esercizio, e anche per convincersi di quanto appena detto,
disegnare i grafici di
 ,
, 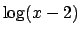 ,
, 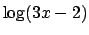 ,
,
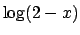 e
e 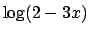 .
.
Abbiamo trasferito quindi il problema nello scrivere lo sviluppo delle
due funzioni 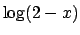 e
e 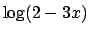 . Si ha, per
. Si ha, per 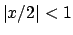 ,
,
Integrando tra  e
e  , con
, con 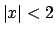 , poiché la serie sopra converge
uniformemente
, poiché la serie sopra converge
uniformemente
e quindi
Analogamente si ottiene, per 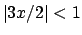 e quindi per
e quindi per 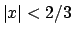 ,
,
Concludendo:
e l'insieme di convergenza è l'intersezione degli insiemi
sui quali convergono separatamente le due serie.
Concludiamo che
e la convergenza è puntuale in 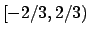 , uniforme in tutti gli insiemi
del tipo
, uniforme in tutti gli insiemi
del tipo ![$[-2/3, a]$](img521.png) con
con
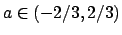 e totale in tutti gli insiemi
del tipo
e totale in tutti gli insiemi
del tipo ![$[b,c]$](img523.png) con
con
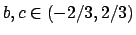 ,
,  .
.
Infatti una delle due serie converge puntualmente almeno in 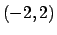 e l'altra
almeno in
e l'altra
almeno in
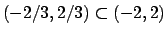 , quindi la serie
converge in
, quindi la serie
converge in 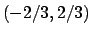 e non converge in
e non converge in
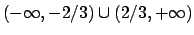 (per verifica calcolare il limite della radice
(per verifica calcolare il limite della radice 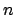 -esima dei coefficienti).
Negli estremi: è sufficiente studiare la seconda serie, poiché convergendo
la prima in
-esima dei coefficienti).
Negli estremi: è sufficiente studiare la seconda serie, poiché convergendo
la prima in 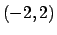 in particolare convergerà in
in particolare convergerà in 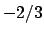 e
e 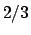 .
Per
.
Per 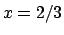 si ha
si ha
che diverge a 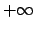 , mentre per
, mentre per 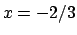 si ha
si ha
che converge.
La convergenza è uniforme in tutti gli intervalli del tipo
![$[-2/3, a]$](img521.png) con
con  e totale negli intervalli del tipo
e totale negli intervalli del tipo
![$[b,c] \subset (-2/3, 2/3)$](img537.png) .
.
Soluzione 1.37 -
L'insieme è ![$[-1,1]$](img208.png) per
per 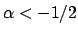 ,
, 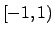 per
per
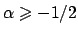 .
.
Soluzione 1.40 -
Si può fare seguendo la soluzione dell'Esercizio 1.36 osservando che
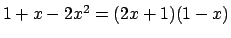 .
.
Soluzione 1.42 -
Attenzione! nella prima serie i coefficienti 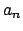 sono dati da
sono dati da 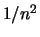 , nella seconda no!
Alcuni infatti sono zero. I coefficienti della seconda serie sono infatti
, nella seconda no!
Alcuni infatti sono zero. I coefficienti della seconda serie sono infatti
Il comportamento però è lo stesso:
infatti la prima converge totalmente in ![$[-1,1]$](img208.png) ;
e la serie converge sia in
;
e la serie converge sia in 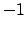 che in
che in 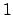 . Per lo studio della seconda, valutando
. Per lo studio della seconda, valutando
si ottiene che la serie converge (assolutamente) per
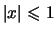 e non converge per
e non converge per 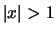 .
La convergenza in
.
La convergenza in ![$[-1,1]$](img208.png) è totale.
è totale.
Soluzione 1.44 -
Si osservi che i termini di questa serie sono ``alcuni'' dei termini della serie
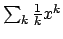 .
Infatti i coefficienti
.
Infatti i coefficienti 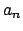 sono dati da
sono dati da
per cui
Di conseguenza il limite
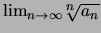 non esiste.
Possiamo trattare la serie come una serie numerica, fissando
non esiste.
Possiamo trattare la serie come una serie numerica, fissando 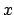 e valutando
e valutando
Passando al limite per 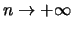 si ottiene che la serie converge per
si ottiene che la serie converge per
![$x \in [-1,1]$](img464.png) .
.
Alternativamente, per chi conoscesse il limsup e che il raggio di convergenza è dato
dal reciproco di
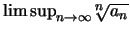 , si ha che
, si ha che
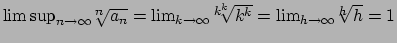 .
Il raggio quindi è
.
Il raggio quindi è 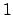 . Per
. Per 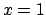 e
e 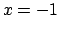 la serie converge e quindi l'insieme
di convergenza è
la serie converge e quindi l'insieme
di convergenza è ![$[-1,1]$](img208.png) . La convergenza è anche totale.
. La convergenza è anche totale.
Soluzione 1.45 -
Questo è un esempio in cui il
limite di
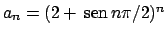 non esiste. Si ha che
non esiste. Si ha che
L'estremo superiore (si veda la definizione di raggio di convergenza nelle dispense)
dei numeri per cui la serie converge è 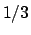 (l'inverso del massimo valore che può assumere
(l'inverso del massimo valore che può assumere
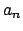 ): infatti non può essere maggiore perché se lo fosse, diciamo
): infatti non può essere maggiore perché se lo fosse, diciamo 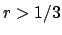 , per tutti i
valori
, per tutti i
valori
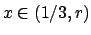 la serie convergerebbe. Ma per infiniti valori di
la serie convergerebbe. Ma per infiniti valori di 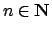 si ha che
si ha che
per cui se fissiamo 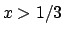 e minore di
e minore di 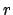 si avrebbe per infinite volte che
si avrebbe per infinite volte che
il che non farebbe convergere la serie.
Soluzione 1.46 -
Poiché la funzione è dispari lo sviluppo è di soli seni.
Si ha
quindi lo sviluppo è
La media di  è nulla, per cui
è nulla, per cui 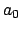 è nullo. Usando la formula (1.2)
si ha che lo sviluppo di
è nullo. Usando la formula (1.2)
si ha che lo sviluppo di
è dato da (i coefficienti  di
di 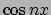 sono nulli, i coefficienti
sono nulli, i coefficienti
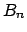 di
di
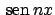 sono dati da
sono dati da 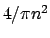 per
per 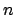 dispari,
dispari, 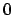 altrimenti)
altrimenti)
dove
![$A_0 = \pi^{-1}\int_{-pi}^{\pi} [\vert x\vert - \pi] dx = -\pi^2/\pi = -\pi$](img570.png) .
Per cui lo sviluppo di
.
Per cui lo sviluppo di 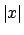 in
in ![$[-\pi, \pi]$](img572.png) è
(confrontare con l'ESERCIZIO 1.49)
è
(confrontare con l'ESERCIZIO 1.49)
Soluzione 1.47 -
La funzione è pari, per cui il suo sviluppo è fatto di soli coseni.
Si ha che
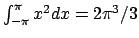 e
e
per cui lo sviluppo è dato da
Poiché l'estensione a tutto  è
è 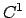 a tratti e continua
si ha convergenza uniforme su tutto
a tratti e continua
si ha convergenza uniforme su tutto  .
In particolare per
.
In particolare per 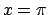 si ha
si ha
da cui si ricava
Soluzione 1.48 -
Il periodo 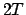 è
è 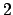 , quindi
, quindi 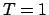 . Calcoliamo i coefficienti:
. Calcoliamo i coefficienti:
quindi lo svilupo è
Converge puntualmente alla funzione
La convergenza uniforme c'è solo negli insiemi del tipo
![$[a,b] \subset (-1,1)$](img228.png) visto che il limite non è continuo.
visto che il limite non è continuo.
Valutiamo ora la serie
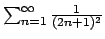 .
Per
.
Per 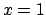 la serie converge al valore
la serie converge al valore 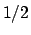 per cui
per cui
da cui
Ora per la somma
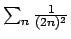 possiamo procedere in due modi:
sfruttare l'esercizio precedente dal quale sappiamo che
possiamo procedere in due modi:
sfruttare l'esercizio precedente dal quale sappiamo che
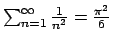 per cui otteniamo
per cui otteniamo
oppure, ignorando il risultato dell'esercizio precedente, osservare
che
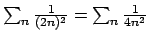 per cui da
per cui da
dedurre che
e quindi
Soluzione 1.49 -
La estendo per periodicità
a tutto  e per questione di semplicità di calcolo sviluppo
la funzione
e per questione di semplicità di calcolo sviluppo
la funzione  definita in
definita in ![$[-\pi, \pi]$](img572.png) ed estesa per periodicità
a tutto
ed estesa per periodicità
a tutto  (si veda la Figura 1.8). In questo modo anziché calcolare
(si veda la Figura 1.8). In questo modo anziché calcolare
Figura 1.8:
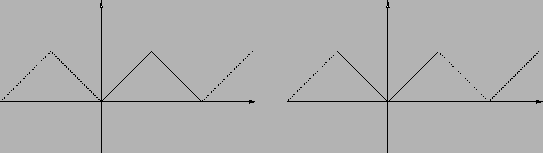 |
calcolo
Quindi i coefficienti sono dati da:
e per 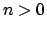
per cui
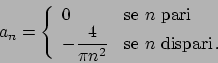 |
(1.4) |
Lo sviluppo risulta quindi essere
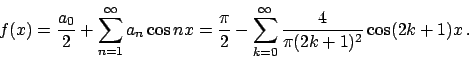 |
(1.5) |
La convergenza è puntuale e uniforme su tutto  (perché la funzione è
continua e
(perché la funzione è
continua e 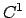 a tratti), in particolare
sull'intervallo
a tratti), in particolare
sull'intervallo ![$[0, 2\pi]$](img608.png) al quale eravamo interessati.
In particolare se valutiamo la serie per
al quale eravamo interessati.
In particolare se valutiamo la serie per 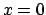 questa convergerà al valore
questa convergerà al valore
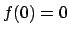 , per cui si ha
, per cui si ha
Per l'altra serie sfruttiamo l'uguaglianza di Parceval (1.1):
Per cui da
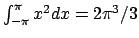 otteniamo
otteniamo
e infine
Per considerare uno sviluppo in soli seni o di soli coseni
in generale si fa così:
data
![$h:[0,T] \to {\bf R}$](img614.png) consideriamo la funzione
consideriamo la funzione 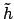 definita
in
definita
in 
ed estendendo poi per periodicità a tutto  la funzione. Poiché la
funzione risulta così pari il suo sviluppo sarà di soli coseni e
la funzione. Poiché la
funzione risulta così pari il suo sviluppo sarà di soli coseni e
Se vogliamo uno sviluppo di soli seni si considera
Nel nostro caso estendiamo la funzione nel modo seguente:
Figura 1.9:
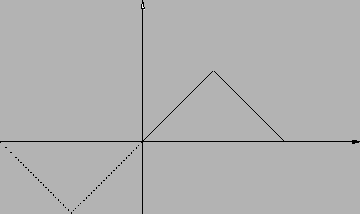 |
e poi estendo 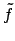 periodicamente su tutto
periodicamente su tutto  (a questo punto avremo
una funzione periodica di periodo
(a questo punto avremo
una funzione periodica di periodo 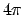 !). La restrizione di
!). La restrizione di 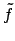 a
a
![$[0, 2\pi]$](img608.png) è sempre la nostra
è sempre la nostra  . La funzione così estesa risulta essere
dispari fornendo i coefficienti dei coseni nulli.
Valutiamo i coefficienti:
. La funzione così estesa risulta essere
dispari fornendo i coefficienti dei coseni nulli.
Valutiamo i coefficienti:
Abbiamo che
per cui
Sommando, poiché
si ha
La serie è data dalla somma dei seguenti termini
Attenzione! Lo sviluppo trovato è lo sviluppo in soli seni della funzione
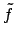 , quello in (1.5) è lo sviluppo della funzione
, quello in (1.5) è lo sviluppo della funzione  :
convergono entrmabi (uniformemente) alla funzione originale nell'intervallo
:
convergono entrmabi (uniformemente) alla funzione originale nell'intervallo
![$[0, 2\pi]$](img608.png) , ma a funzioni diverse nell'intervallo
, ma a funzioni diverse nell'intervallo ![$[-2\pi, 0]$](img630.png) (si vedano le Figura 1.8 e Figura 1.9).
(si vedano le Figura 1.8 e Figura 1.9).
Ora valutiamo lo sviluppo della funzione 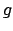 : si osservi che nell'intervallo
: si osservi che nell'intervallo ![$[-\pi, \pi]$](img572.png) la funzione
la funzione 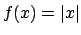 è una primitiva della funzione
è una primitiva della funzione 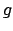 , e precisamente
, e precisamente
Se denotiamo con 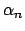 e
e  i coefficienti
i coefficienti
si ha che 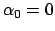 e dalle formule (1.2) si ricava
e dalle formule (1.2) si ricava
quindi, conoscendo 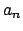 (si veda (1.4)) e
(si veda (1.4)) e 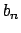 (
(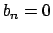 per ogni
per ogni 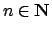 ) si ricava immediatamente
) si ricava immediatamente
per cui
(si confronti con l'ESERCIZIO 1.46).
Soluzione 1.50 -
La funzione
come si vede dal garfico,
è una funzione pari per cui 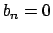 per ogni
per ogni 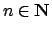 .
.
Figura 1.10:
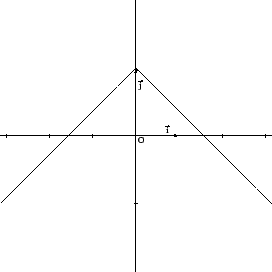 |
Si verifica facilmente che anche 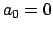 . Gli altri coefficienti
sono dati (
. Gli altri coefficienti
sono dati (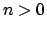 )
)
per cui la serie è data da
che converge uniformemente su tutto  (visto che il prolungamento periodico
a tutto
(visto che il prolungamento periodico
a tutto  di
di  è continuo e
è continuo e 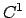 a tratti). La serie converge anche
totalmente visto che
a tratti). La serie converge anche
totalmente visto che
Per calcolare le due serie (già calcolate negli esercizi
1.48 e 1.49) si può valutare la funzione in 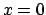 e usare
l'uguaglianza (1.1).
e usare
l'uguaglianza (1.1).



Next: About this document ...
Up: 1esercizi
Previous: 1esercizi
Fabio Paronetto
2005-05-06
![]() tali che
tali che
![]() .
Ci chiediamo se il limite è anche uniforme: dovrei avere che
.
Ci chiediamo se il limite è anche uniforme: dovrei avere che


![\begin{esercizio}\rm -\
Studiare convergenza puntuale ed uniforme di
$f_n: [0,1] \to {\bf R}$, $f_n(x) = {\displaystyle {{nx}\over{1+n^2x^2}}}$.
\end{esercizio}](img26.png)



![\begin{esercizio}\rm -\
Si studi la convergenza puntuale ed uniforme in $[-1, 1]...
...gin{displaymath}
f_n(x) = n \log (1 + x/n) .
\end{displaymath}\end{esercizio}](img30.png)
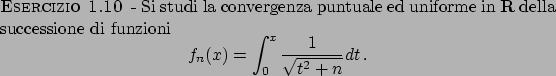
![]() è una speciale successione di funzioni
è una speciale successione di funzioni
![]() dove
dove
![]() .
.

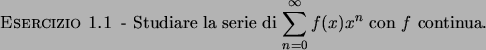


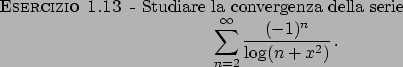


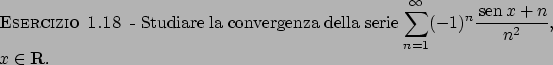
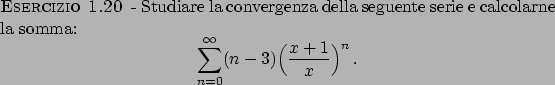
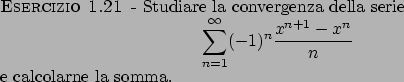

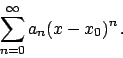
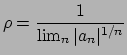 se tale limite esiste
(si vedano le dispense di teoria per la definizione di raggio di convergenza
e l'Esercizio 1.45 per un esempio in cui il limite non
esiste).
se tale limite esiste
(si vedano le dispense di teoria per la definizione di raggio di convergenza
e l'Esercizio 1.45 per un esempio in cui il limite non
esiste).

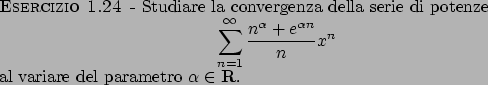
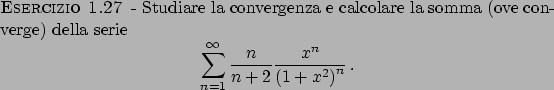
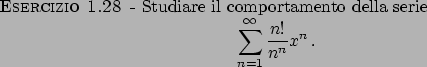
![\begin{esercizio}\rm -\
Studiare la convergenza e calcolare la somma di
\begin{d...
...}\over{n!}} - {{1}\over{(n+1)!}} \Big] x^n .
\end{displaymath}\end{esercizio}](img65.png)
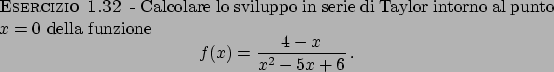
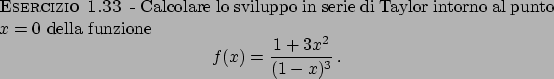




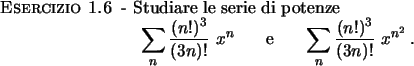
![]() è il semiperiodo la serie è data da
è il semiperiodo la serie è data da
![\begin{displaymath}
{{a_0}\over{2}} + \sum_{n=1}^{\infty} \Big[a_n \cos {{n \pi}\over{T}}x
+ a_n \!\textrm{sen} \!{{n \pi}\over{T}}x \Big]
\end{displaymath}](img78.png)
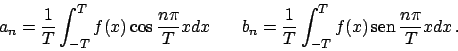
![\begin{displaymath}
\sup_{x\in [-1,1]} \Big\vert {\displaystyle \sqrt{x^2 + {{1}...
...\sup_{x\in [-1,1]} \sqrt{{{1}\over{n}}} = \sqrt{{{1}\over{n}}}
\end{displaymath}](img100.png)
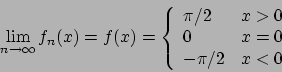
![]()
![]() è una successione di funzioni continue che converge puntualmente
ad una funzione
è una successione di funzioni continue che converge puntualmente
ad una funzione ![]() non continua, la convergenza non può essere uniforme.
non continua, la convergenza non può essere uniforme.
![]()
![]() non converge uniformemente ad
non converge uniformemente ad ![]() .
Ci si può chiedere se ci sono insiemi strettamente contenuti in
.
Ci si può chiedere se ci sono insiemi strettamente contenuti in ![]() sui quali la
convergenza è uniforme.
Si consideri
sui quali la
convergenza è uniforme.
Si consideri
![]() con
con ![]() .
La derivata di
.
La derivata di
![]() è sempre negativa
(per cui non ci sono punti stazionari).
Questo però ci dice che il massimo è assunto per
è sempre negativa
(per cui non ci sono punti stazionari).
Questo però ci dice che il massimo è assunto per ![]() . Per cui
. Per cui
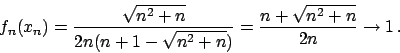
![\begin{displaymath}
\vert f_n(x) - f(x)\vert =
\left\{
\renewcommand {\arraystr...
...yle {{-x(1-x)}\over{x^2+n}}} & x \in [1, b]
\end{array}\right.
\end{displaymath}](img132.png)
![\begin{displaymath}
\sup_{x\in [0,a]} \vert f_n(x)\vert = {{a^2}\over{a+n}} \to 0
\hskip20pt \textrm{per ogni }a \in (0, + \infty) .
\end{displaymath}](img154.png)
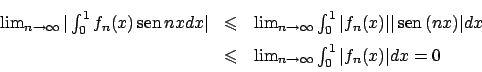
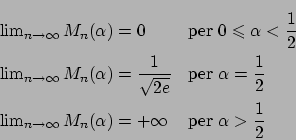
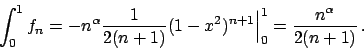
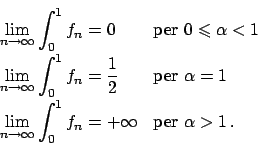
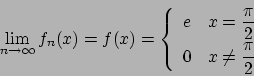
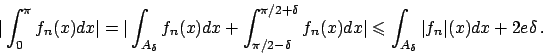

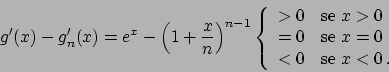
![\begin{teorema}
Sia $(f_n)_n$ una successione in $C^1([a,b])$ tale che
\begin{...
...mente ad una funzione $f$.
Inoltre $f \in C^1([a,b])$ e $f' = g$.
\end{teorema}](img215.png)
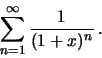

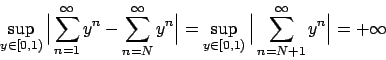
![\begin{displaymath}
\sup_{y \in (-1,0]} \Big\vert \sum_{n=1}^{\infty} y^n - \sum...
...\in [0,1)} \Big\vert {{y^{N+1}}\over{1-y}} \Big\vert = +\infty
\end{displaymath}](img230.png)
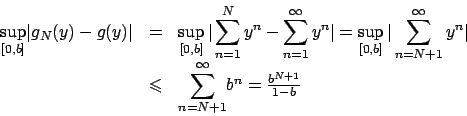
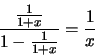
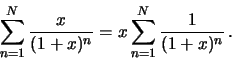
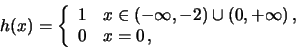
 ?
?
 si procede come
nella soluzione dell'ESERCIZIO 1.11 per ottenere la convergenza puntuale
in
si procede come
nella soluzione dell'ESERCIZIO 1.11 per ottenere la convergenza puntuale
in 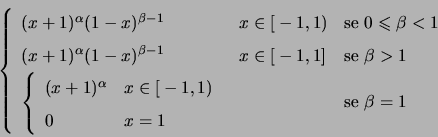
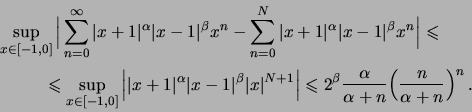
![\begin{displaymath}
\renewcommand {\arraystretch}{1.5}
\begin{array}{l}
{\displa...
...sup_{x \in [0,1]} (x+1)^{\alpha}(1-x)^{\beta-1}x^N}
\end{array}\end{displaymath}](img305.png)
 , proposta alla fine
della soluzione dell'ESERCIZIO 1.11, si può concludere che
la serie converge uniformemente in
, proposta alla fine
della soluzione dell'ESERCIZIO 1.11, si può concludere che
la serie converge uniformemente in 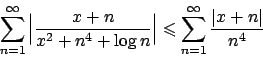
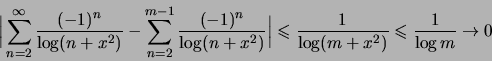
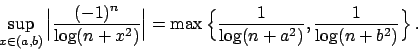


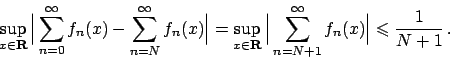
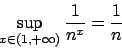
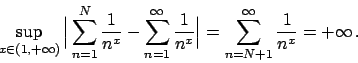
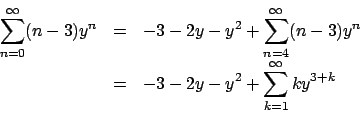
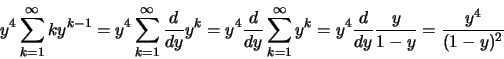
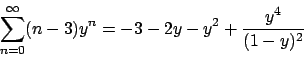
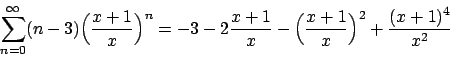
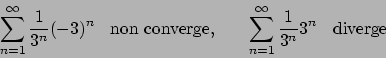
![]()
![]() con
con ![]() . Vediamo se si ha convergenza uniforme anche in
. Vediamo se si ha convergenza uniforme anche in
![]() .
Ragionando come al solito (si veda, ad esempio, la risoluzione
dell'esercizio 1.11) si deduce che la serie non può convergere
uniformemente in
.
Ragionando come al solito (si veda, ad esempio, la risoluzione
dell'esercizio 1.11) si deduce che la serie non può convergere
uniformemente in ![]() e quindi nemmeno totalmente.
e quindi nemmeno totalmente.
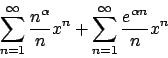

![]() con
con
![]() , non abbiamo convergenza uniforme, e quindi nemmeno totale,
in
, non abbiamo convergenza uniforme, e quindi nemmeno totale,
in ![]() . Vediamo in
. Vediamo in ![]() : qui la serie è a segni alterni, per vedere se
la serie è uniformemente convergente uso il criterio di Leibniz. Detta
: qui la serie è a segni alterni, per vedere se
la serie è uniformemente convergente uso il criterio di Leibniz. Detta
![]() la somma della serie e
la somma della serie e ![]() le somme parziali devo vedere se vale
le somme parziali devo vedere se vale
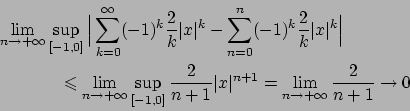
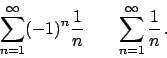
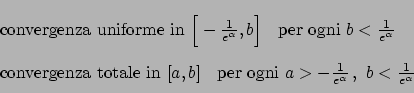
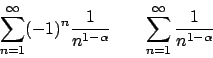
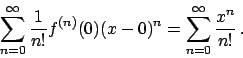

![\begin{displaymath}
{\displaystyle
\sup_{x \in (-\infty, 0]} \Big\vert \sum_{k=...
...p_{x \in (-\infty, 0]} \vert e^x - p_n(x)\vert = + \infty .
\end{displaymath}](img420.png)
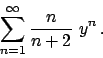
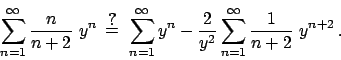
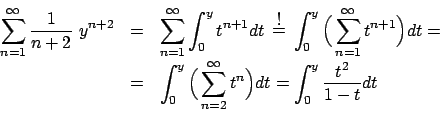
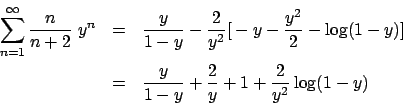
![\begin{displaymath}
\renewcommand {\arraystretch}{2}
\begin{array}{lll}
{\displa...
...y^3}\over{1-y}} + 2y + y^2 - 2y +y^2 +o(y^2) \Big]}
\end{array}\end{displaymath}](img440.png)
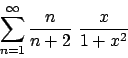
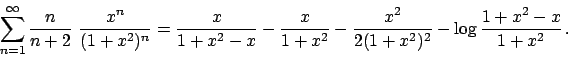

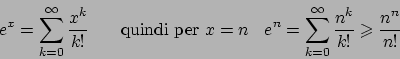
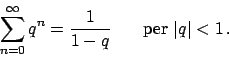
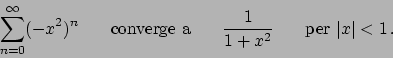
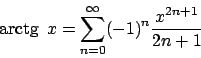
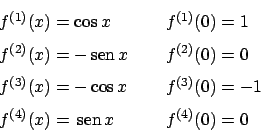
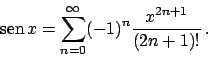


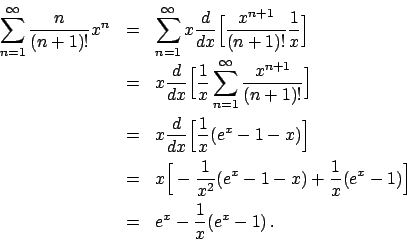
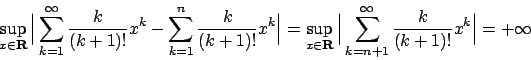
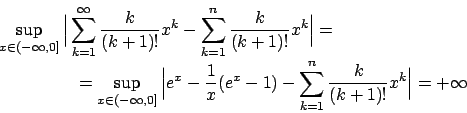
![]() ).
Per
).
Per ![]() con
con ![]() positivo
positivo
![]() come prodotto di
come prodotto di ![]() e
e ![]() si ottiene che
si ottiene che
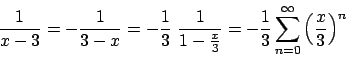
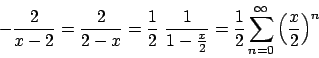
![\begin{displaymath}
f(x) = \sum_{n=0}^{\infty} \Big[ {{1}\over{2^{n+1}}} - {{1}\over{3^{n+1}}} \Big] x^n .
\end{displaymath}](img495.png)
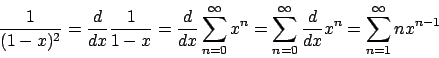
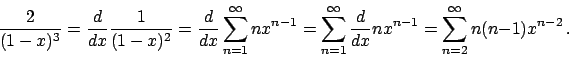
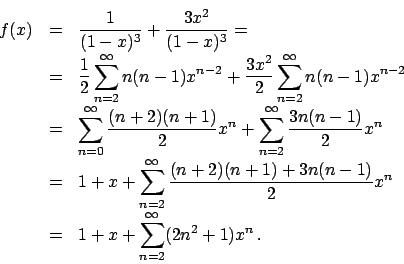
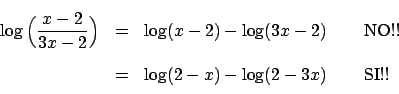
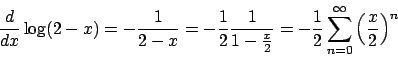
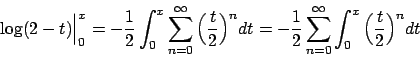
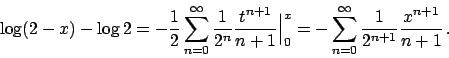
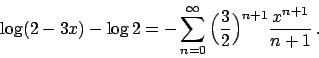
![\begin{displaymath}
\renewcommand {\arraystretch}{2}
\begin{array}{lll}
{\displa...
...({{1}\over{2}}\Big)^{n} \Big] {{x^{n+1}}\over{n}} }
\end{array}\end{displaymath}](img518.png)
![\begin{displaymath}
\log \Big[ {{x-2}\over{3x-2}} \Big] =
\sum_{n=1}^{\infty} \B...
...({{3}\over{2}}\Big)^n - {{1}\over{2^n}} \Big]
{{x^n}\over{n}}
\end{displaymath}](img519.png)
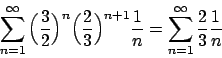
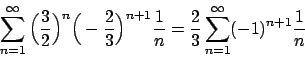
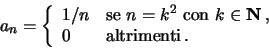
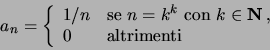

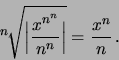
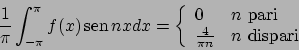
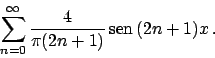
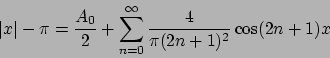
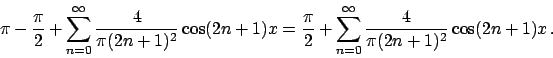
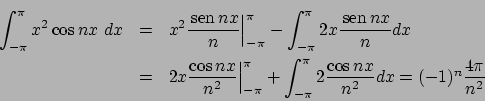
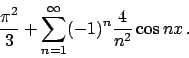
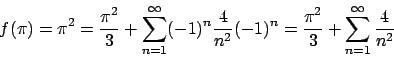

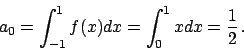
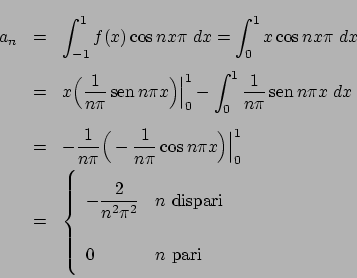
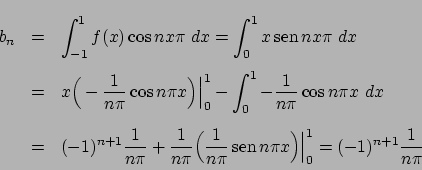
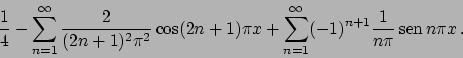

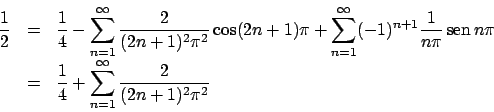
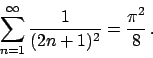
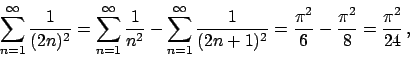
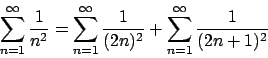
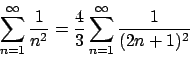
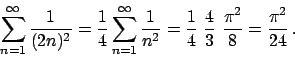
![\begin{displaymath}
\renewcommand {\arraystretch}{2}
\begin{array}{lll}
a_n & = ...
... _0^{\pi} \Big]
= {{2}\over{\pi n^2}}} [(-1)^n - 1]
\end{array}\end{displaymath}](img605.png)
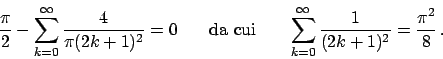
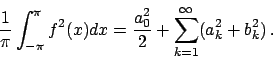
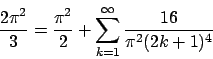
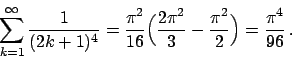
![\begin{displaymath}
\tilde{h}(x) = \left\{
\begin{array}{ll}
h(x) & x \in [0,T] \\
h(-x) & x \in [-T, 0]
\end{array} \right.
\end{displaymath}](img617.png)
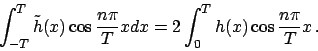
![\begin{displaymath}
\tilde{h}(x) = \left\{
\begin{array}{ll}
h(x) & x \in [0,T] \\
-h(-x) & x \in [-T, 0] .
\end{array} \right.
\end{displaymath}](img619.png)
![\begin{displaymath}
\tilde{f}(x) = \left\{
\begin{array}{cl}
-x - 2 \pi & \tex...
... + 2 \pi & \textrm{se } x \in [\pi, 2\pi]
\end{array} \right.
\end{displaymath}](img621.png)
![\begin{displaymath}
\renewcommand {\arraystretch}{2}
\begin{array}{lll}
b_n & = ...
... \pi] \!\textrm{sen} \!{{n}\over{2}} x dx} .
\end{array}\end{displaymath}](img623.png)
![\begin{displaymath}
\renewcommand {\arraystretch}{2}
\begin{array}{lll}
\textrm{...
...}\over{n}} \cos {{n \pi}\over{2}}\Big) \Big] } .
\end{array}\end{displaymath}](img625.png)
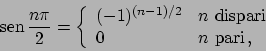
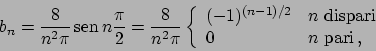
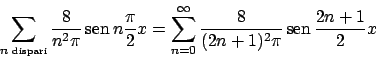
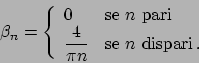
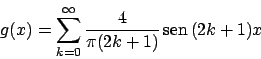
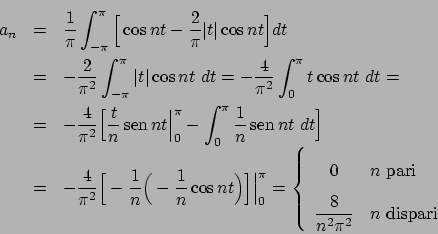
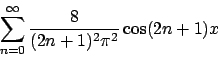
![\begin{displaymath}
\sup_{x \in [-\pi, \pi]} \Big\vert {{8}\over{(2n+1)^2 \pi^2}} \cos (2n+1)x \Big\vert
= {{8}\over{(2n+1)^2 \pi^2}} .
\end{displaymath}](img646.png)