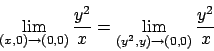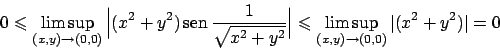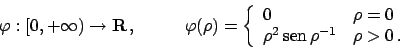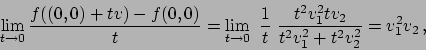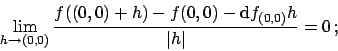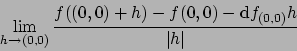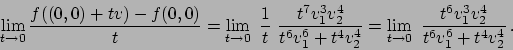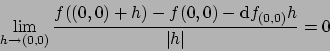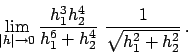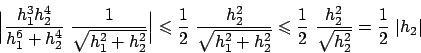Next: About this document ...
Up: 2esercizi
Previous: 2esercizi
ULTIMO AGGIORNAMENTO: 19. aprile 2004
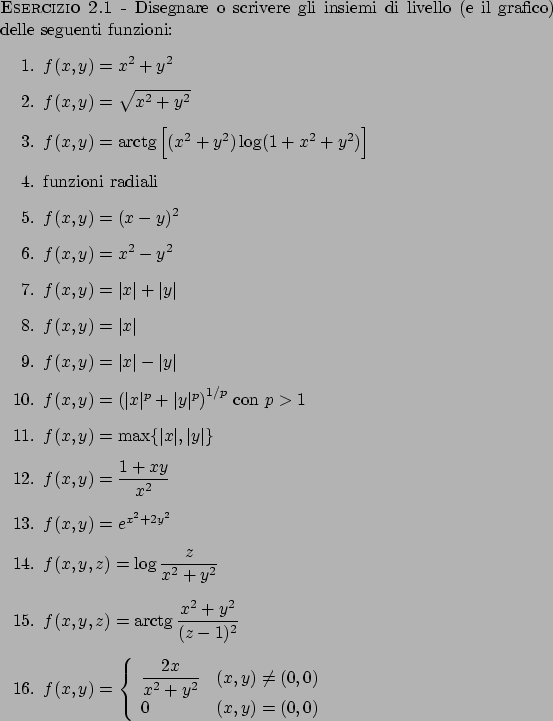


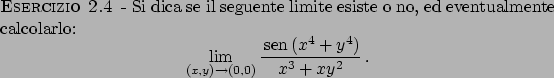
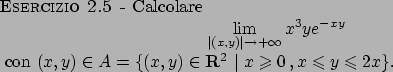
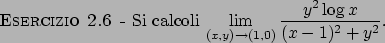
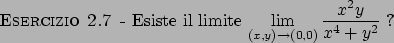

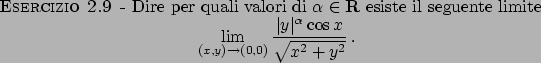



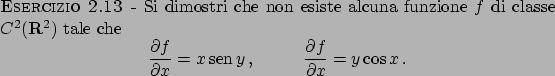



Soluzioni
Soluzione 2.1 -
Denotiamo con  ,
, 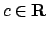 , l'insieme di livello
, l'insieme di livello 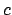 , in questo caso
l'insieme
, in questo caso
l'insieme
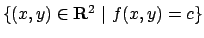 .
Dobbiamo risolvere
.
Dobbiamo risolvere 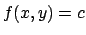 con
con 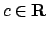 . È evidente che per
. È evidente che per 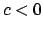 l'insime
l'insime
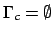 . Per
. Per 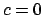
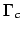 è fatto da un solo punto
è fatto da un solo punto
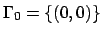 . Per
. Per 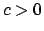 si hanno circonferenze di raggio
si hanno circonferenze di raggio 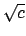 .
.
- 1.
- In generale per una funzione radiale, cioè che dipende solamente dalla distanza
dall'origine, gli insiemi di livello possono essere l'insieme vuoto
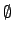 , insiemi
fatti da un solo punto oppure circonferenze in
, insiemi
fatti da un solo punto oppure circonferenze in 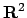 , sfere in
, sfere in 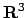 (ipersfere di codimensione
(ipersfere di codimensione 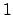 in
in 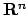 ).
Possono essere anche corone circolari o tutto
).
Possono essere anche corone circolari o tutto 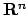 o unione di più circonferenze.
In generale si pensi ad una funzione radiale come ad
una funzione radiale
o unione di più circonferenze.
In generale si pensi ad una funzione radiale come ad
una funzione radiale
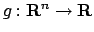 definita tramite
un'altra funzione
definita tramite
un'altra funzione
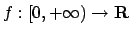 nel modo seguente:
nel modo seguente:
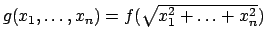 .
.
- 5.
-
 se
se  . Se
. Se  dobbiamo capire qual è l'insieme rappresentato
da
dobbiamo capire qual è l'insieme rappresentato
da 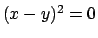 . È dato dai punti di
. È dato dai punti di 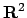 che stanno sulla retta di equazione
che stanno sulla retta di equazione
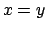 . Se invece
. Se invece 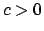 si ha
si ha
quindi l'insieme di livello 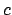 con
con 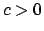 è dato da coppie di rette
è dato da coppie di rette
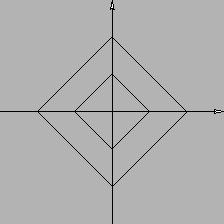
- 7.
- Risolvendo
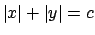 si ha per
si ha per 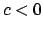 l'insieme
l'insieme 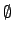 , per
, per 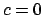 il solo punto
il solo punto 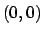 , per
, per 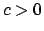 le curve in Figura 2.1
le curve in Figura 2.1
Figura 2.1:
 |
- 11.
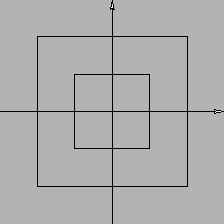
- Risolvendo
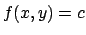 si ha per
si ha per 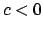 l'insieme
l'insieme 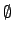 , per
, per 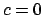 il solo punto
il solo punto 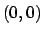 , per
, per 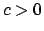 le curve in Figura 2.2
le curve in Figura 2.2
Figura 2.2:
 |
- 12.
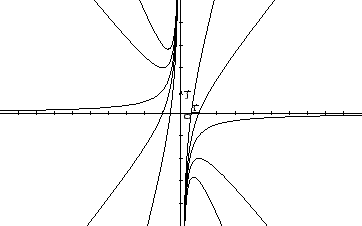
- Risolviamo
Innanzitutto deve essere 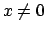 . Si ottiene (si veda anche Figura 2.3
per alcune curve di livello)
. Si ottiene (si veda anche Figura 2.3
per alcune curve di livello)
Figura 2.3:
 |
- 14.
- Sia
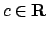 e poniamo
e poniamo 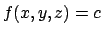 . Ciò è equivalente a
. Ciò è equivalente a
con 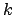 costante positiva. Gli insiemi di livello sono quindi paraboloidi
di equazione
costante positiva. Gli insiemi di livello sono quindi paraboloidi
di equazione
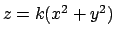 con
con 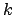 costante positiva.
costante positiva.
- 16.
- Se
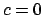 linsieme di livello è fatto dal solo punto
linsieme di livello è fatto dal solo punto 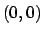 . Sia quindi
. Sia quindi 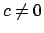 :
ponendo
:
ponendo
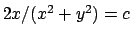 si ottiene
si ottiene
che, al variare di 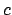 in
in 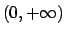 e in
e in 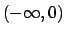 , rappresentano delle
circonferenze di raggio
, rappresentano delle
circonferenze di raggio 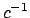 con centro nel punto
con centro nel punto 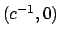 come rappresentato
in Figura 2.4.
come rappresentato
in Figura 2.4.
Figura 2.4:
 |
Soluzione 2.2 -
Se il limite esistesse in particolare si avrebbe
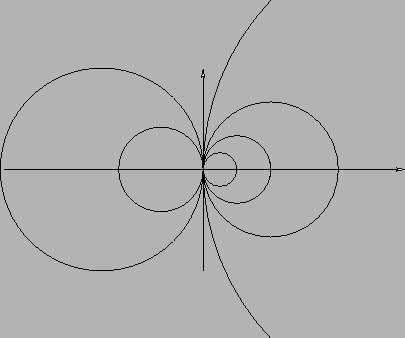
ma il primo limite è uguale a 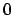 , il secondo a
, il secondo a 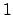 . Esistono curve lungo le quali
il limite è
. Esistono curve lungo le quali
il limite è 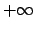 ?
?
Soluzione 2.3 -
Ricordo: se una funzione è di classe 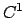 sicuramente è differenziabile, ma non è detto
che il viceversa sia vero: ecco un esempio in cui ciò non accade.
sicuramente è differenziabile, ma non è detto
che il viceversa sia vero: ecco un esempio in cui ciò non accade.
È chiaramente continua in ogni
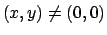 . Vediamo se lo è anche
in
. Vediamo se lo è anche
in 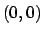 . Se il limite esiste si ha
. Se il limite esiste si ha
per cui il limite
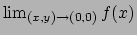 esiste ed è zero. Poiché
esiste ed è zero. Poiché
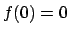 concludiamo che
concludiamo che 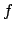 è continua.
è continua.
Per studiare la derivabilità e la differenziabilità si osservi prima che la funzione è
radiale: possiamo infatti esprimerla come
dove
La funzione 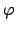 estesa per simmetria anche a
estesa per simmetria anche a 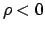 (
(
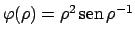 per
per 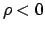 ) è derivabile in
) è derivabile in 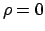 (e ovviamente anche per gli altri valori di
(e ovviamente anche per gli altri valori di 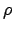 ): infatti il calcolo del limite del rapporto
incrementale è
): infatti il calcolo del limite del rapporto
incrementale è
Ma se calcoliamo la derivata in un altro punto si ottiene
il cui limite per 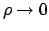 non esiste. Concludiamo che la derivata esiste, ma non è
continua nel punto
non esiste. Concludiamo che la derivata esiste, ma non è
continua nel punto 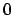 . Questo si traduce per la funzione
. Questo si traduce per la funzione 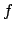 nel fatto che
nel fatto che 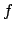 è differenzibile in
è differenzibile in 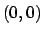 , e il suo differenziale in quel punto è l'applicazione nulla,
ma le derivate, che esistono, non sono continue nel punto
, e il suo differenziale in quel punto è l'applicazione nulla,
ma le derivate, che esistono, non sono continue nel punto 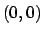 .
.
Soluzione 2.4 -
Si noti che
mentre
quindi il limite non esiste.
Soluzione 2.5 -
In  vale la seguente stima
vale la seguente stima
da cui otteniamo
quindi
Poiché
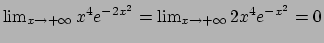 si conclude che
si conclude che
Soluzione 2.6 -
Usiamo le coordinate polari:
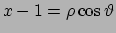 ,
,
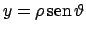 .
Vale:
.
Vale:
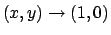 se e solo se
se e solo se
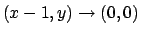 se e solo se
se e solo se 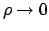 indipendentemente da
indipendentemente da 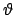 .
Il limite, se esiste, può essere quindi riscritto nelle nuove variabili
come segue
.
Il limite, se esiste, può essere quindi riscritto nelle nuove variabili
come segue
Attenzione! Non sempre l'uso delle coordinate polari è di aiuto nello
svolgere i limiti (si veda ad esempio la soluzione dell'esercizio 2.7).
Soluzione 2.7 -
Se si passa in coordinate polari si ottiene
che non esiste!! Se esistesse dovrebbe essere indipendente dal valore di 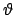 .
Ad esempio
.
Ad esempio
Soluzione 2.8 -
Si può mostrare che esiste 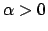 tale che
tale che
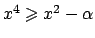 (si veda per esercizio che la disuguaglianza vale con
(si veda per esercizio che la disuguaglianza vale con 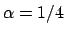 .
È il valore minore?).
Quindi
.
È il valore minore?).
Quindi
Sia
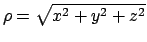 . Si ha, poiché
. Si ha, poiché
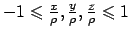 ,
,
e
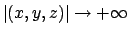 significa
significa
 per cui il limite è
per cui il limite è 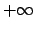 .
.
Soluzione 2.9 -
Passando alle coordinate polari si ha
che è uguale a 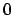 se
se 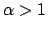 . Per
. Per
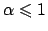 il limite non esiste: infatti
se si considerano, ad esempio, prima
il limite non esiste: infatti
se si considerano, ad esempio, prima 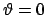 e poi
e poi
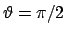 e poi si esegue il
limite per
e poi si esegue il
limite per 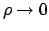 si ottengono due risultati diversi.
si ottengono due risultati diversi.
Soluzione 2.10 -
Ovviamente l'unico punto in cui fare le verifiche è l'origine in quanto negli altri punti
la funzione è differenziabile.
In coordinate polari la funzione diventa (per 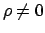 )
)
e
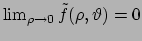 ,
, 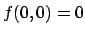 per cui
per cui 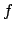 risulta continua
anche nell'origine. Vediamo se è derivabile: fissiamo un vettore
risulta continua
anche nell'origine. Vediamo se è derivabile: fissiamo un vettore
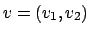 di norma
di norma 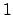 (
(
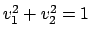 ) e calcoliamo il limite
) e calcoliamo il limite
di conseguenza esistono le derivate direzionali in ogni direzione e si ha
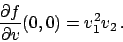 |
(2.1) |
Vediamo ora se 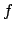 è differenziabile nel punto
è differenziabile nel punto 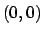 . Se lo è deve esistere
un'applicazione lineare
. Se lo è deve esistere
un'applicazione lineare 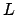 , denotata anche con
, denotata anche con
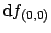 , tale che
, tale che
inoltre la differenziabilità implica (si veda Osservazione 3.4 delle dispense di teoria)
l'esistenza di tutte le derivate parziali e direzionali e
Poiché l'applicazione deve essere lineare, e l'applicazione in (2.1) non lo è,
si deduce che 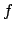 non può essere differenziabile.
non può essere differenziabile.
(Per convincersi si effettui comunque il calcolo del limite
sostituendo al differenziale il valore del gradiente moltiplicato scalarmente
per un vettore 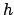 , sapendo da (2.1) che le derivate parziali sono entrambe nulle).
, sapendo da (2.1) che le derivate parziali sono entrambe nulle).
Soluzione 2.11 -
Si ha
visto che
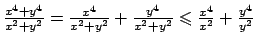 .
Usando questa disuguaglianza si mostra che
.
Usando questa disuguaglianza si mostra che 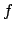 è continua, derivabile, differenziabile
(il differenziale è l'applicazione nulla).
è continua, derivabile, differenziabile
(il differenziale è l'applicazione nulla).
Soluzione 2.12 -
Risposta:
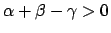 (suggerimento: usare le coordiante polari).
(suggerimento: usare le coordiante polari).
Soluzione 2.13 -
Non esistono.
Soluzione 2.14 -
In
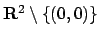 è continua, derivabile, differenziabile. Per vedere la
continuità nell'origine si osservi che
è continua, derivabile, differenziabile. Per vedere la
continuità nell'origine si osservi che
(abbiamo usato la disuguaglianza
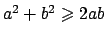 ,
,
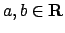 : mostrarla per esercizio).
Quindi
: mostrarla per esercizio).
Quindi
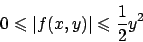 |
(2.2) |
e di conseguenza
Vediamo la derivabilità: sia 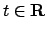 e
e 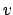 vettore di norma
vettore di norma 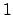 :
:
Questo limite è zero: si ricordi infatti che 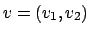 è fissato.
Se
è fissato.
Se 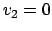 la quantità
la quantità
 è identicamente nulla, se
è identicamente nulla, se 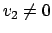 il limite è zero. Si può vedere in altro modo sfruttando la stima (2.2)
il limite è zero. Si può vedere in altro modo sfruttando la stima (2.2)
Analogamente si mostra la differenziabilità:
poiché le derivate parziali sono nulle l'applicazione lineare candidata a rappresentare il
differenziale è l'applicazione nulla. Quindi per verificare che
è sufficiente calcolare
Si ha, usando ancora la stima (2.2)
e quindi passando al limite per 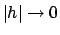 si conclude.
si conclude.
Soluzione 2.15 -
Se esistesse, per il teorema di Schwarz, si avrebbe che
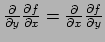 , ma è semplice verificare
che ciò non è vero.
, ma è semplice verificare
che ciò non è vero.



Next: About this document ...
Up: 2esercizi
Previous: 2esercizi
Fabio Paronetto
2004-04-19
![]() ,
, ![]() , l'insieme di livello
, l'insieme di livello ![]() , in questo caso
l'insieme
, in questo caso
l'insieme
![]() .
Dobbiamo risolvere
.
Dobbiamo risolvere ![]() con
con ![]() . È evidente che per
. È evidente che per ![]() l'insime
l'insime
![]() . Per
. Per ![]()
![]() è fatto da un solo punto
è fatto da un solo punto
![]() . Per
. Per ![]() si hanno circonferenze di raggio
si hanno circonferenze di raggio ![]() .
.