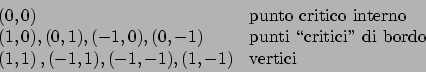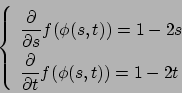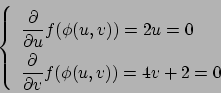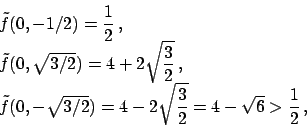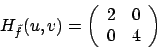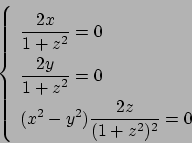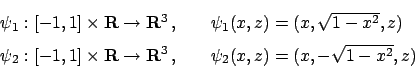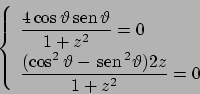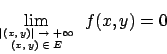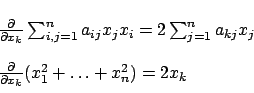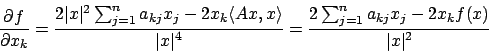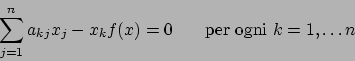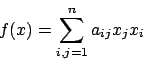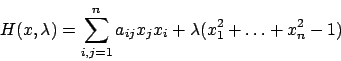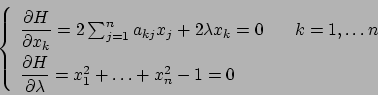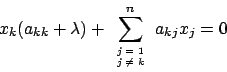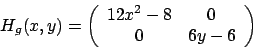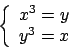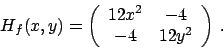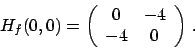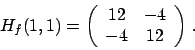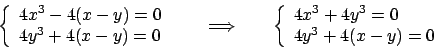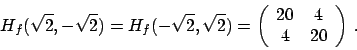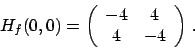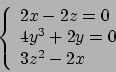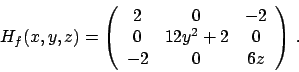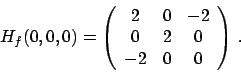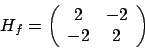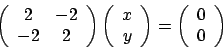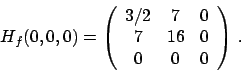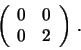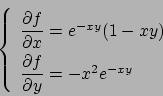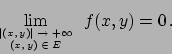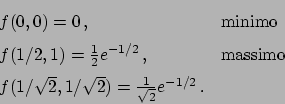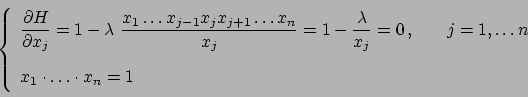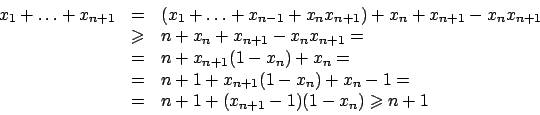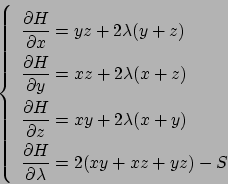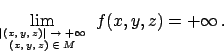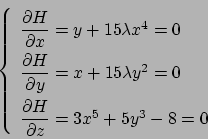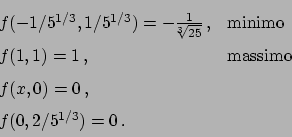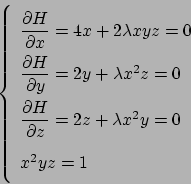Next: About this document ...
Up: 3esercizi
Previous: 3esercizi
ULTIMO AGGIORNAMENTO: 23. giugno 2005
Ricordiamo i seguenti risultati (si vedano rispettivamente
il Teorema 2.39 e Teorema 3.19 delle dispense).
Teorema A Una funzione
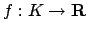 continua in
continua in  compatto di
compatto di 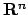 .
ammette sia massimo che minimo.
.
ammette sia massimo che minimo.
Teorema B Sia
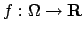 ,
, 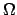 aperto di
aperto di 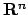 ,
,
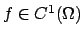 .
Se
.
Se
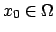 è un punto di minimo o di massimo per
è un punto di minimo o di massimo per  allora
allora
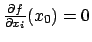 per
per 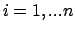 .
.
Esempi
- a)
- Le ipotesi del Teorema A sono ottimali.
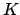 limitato, ma non chiuso,
limitato, ma non chiuso,  continua - Ad esempio
continua - Ad esempio
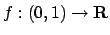 ,
, 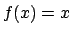 , non ammette né massimo né minimo.
, non ammette né massimo né minimo.
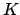 chiuso, ma non limitato,
chiuso, ma non limitato,  continua -
Ad esempio
continua -
Ad esempio
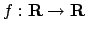 ,
,
 ,
non ammette né massimo né minimo.
,
non ammette né massimo né minimo.
 non continua e
non continua e 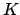 compatto - Ad esempio,
compatto - Ad esempio,
![$f : [-1,1] \to {\bf R}$](img15.png) definita da
definita da
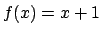 per
per 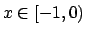 ,
, 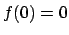 mentre
mentre 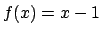 per
per
![$x \in (0, 1]$](img20.png) .
.
- b)
- Le informazioni che si ottengono da
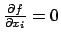 riguardano solo i punti interni, quindi se non si trovano soluzioni a tale sistema di
equazioni non significa che non ci siano il massimo e il minimo.
riguardano solo i punti interni, quindi se non si trovano soluzioni a tale sistema di
equazioni non significa che non ci siano il massimo e il minimo.
- Ad esempio
![$f:[0,1] \to {\bf R}$](img22.png) ,
, 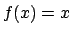 , ha derivata sempre non nulla all'interno di
, ha derivata sempre non nulla all'interno di ![$[0,1]$](img23.png) e comunque ammette sia massimo che minimo.
e comunque ammette sia massimo che minimo.
Vediamo schematicamente una traccia di come procedere
per trovare i punti di massimo e di minimo per una funzione di più variabili
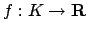 (in alcune situazioni):
(in alcune situazioni):
se 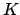 è compatto (cioè limitato e chiuso):
è compatto (cioè limitato e chiuso):
- prima si cercano eventuali candidati all'interno di
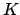 risolvendo,
dove
risolvendo,
dove  è differenziabile,
le equazioni
è differenziabile,
le equazioni
- poi si considera il bordo di
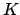 , parametrizzandolo
(il bordo può avere parti di dimensione
, parametrizzandolo
(il bordo può avere parti di dimensione 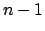 ,
, 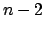 , ...
, ... 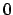 )
oppure usando il metodo dei moltiplicatori di Lagrange.
)
oppure usando il metodo dei moltiplicatori di Lagrange.
Se esistono punti all'interno di 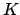 nei quali
nei quali  non è differenziabile
e l'insieme in cui
non è differenziabile
e l'insieme in cui  non è differenziabile è unione di
parti di dimensione
non è differenziabile è unione di
parti di dimensione 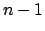 ,
, 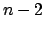 , ...
, ... 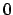 queste vanno trattate come si tratta il
bordo;
queste vanno trattate come si tratta il
bordo;
- si valuta la funzione nei punti trovati (al punto 1. e al punto 2.)
e nei punti del bordo di dimensione
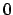 ,
i ``vertici'', se questi sono un numero finito, per vedere qual è il massimo e il
minimo della funzione; se invece si vuole studiare la natura di ogni singolo
punto si può studiare la matrice hessiana
nei punti interni se
,
i ``vertici'', se questi sono un numero finito, per vedere qual è il massimo e il
minimo della funzione; se invece si vuole studiare la natura di ogni singolo
punto si può studiare la matrice hessiana
nei punti interni se  è sufficientemente regolare.
è sufficientemente regolare.
Se 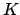 non è limitato:
non è limitato:
- 4.
- si procede come ai punti 1., 2., 3. e in più va controllato il comportamento
all'infinito (dentro
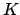 ) della funzione.
) della funzione.
Curve di livello:
- un modo differente per trovare i massimi e minimi è quello di studiare gli insiemi
di livello della funzione, cosa che talvolta risulta più semplice e
può evitare di fare calcoli inutilmente
(si veda, ad esempio, lo svolgimento dell'ESERCIZIO 3.4,
ma anche 3.11, 3.12, 3.13).
Osservazione -
A volte un problema di massimo o minimo
può essere modificato per semplificare i calcoli.
Sia
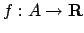 la funzione di cui si vogliono trovare il valore minimo e il valore
massimo e siano
la funzione di cui si vogliono trovare il valore minimo e il valore
massimo e siano 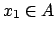 punto di minimo,
punto di minimo, 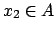 punto di massimo, cioè
punto di massimo, cioè
Se
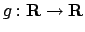 è una funzione monotona crescente si avrà
è una funzione monotona crescente si avrà
Quindi il punto di minimo (e non il valore minimo!) di
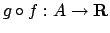 è lo stesso della funzione
è lo stesso della funzione  (idem per il massimo).
Di conseguenza il problema può essere trasformato nel cercare
il punto di minimo e il punto di massimo per una
funzione
(idem per il massimo).
Di conseguenza il problema può essere trasformato nel cercare
il punto di minimo e il punto di massimo per una
funzione 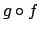 per un'opportuna
per un'opportuna 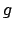 (si vedano ad esempio gli svolgimenti dell'ESERCIZIO 3.4 e
dell'ESERCIZIO 3.14).
(si vedano ad esempio gli svolgimenti dell'ESERCIZIO 3.4 e
dell'ESERCIZIO 3.14).
Suggerimenti -
Anche se viene scelta (per motivi didattici) e proposta una soluzione non è detto
che questa sia l'unica o la migliore.
Consigliamo, quindi, di svolgere in più modi, quando possibile, i vari esercizi.
Un'altra cosa: a volte può essere vantaggioso usare il metodo dei moltiplicatori di Lagrange
(si vedano, ad esempio, l'ESERCIZIO 3.25, 3.26, 3.27), ma in generale,
se possibile, per trovare gli estremi di una funzione sul bordo di un
insieme (o in generale su un vincolo) consigliamo di parametrizzare,
abbassando così il numero di parametri invece di
aumentarlo.
Massimi e minimi su compatti


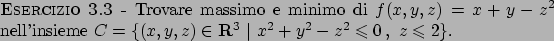
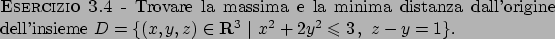
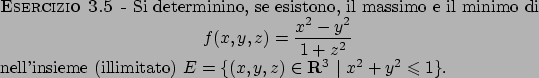
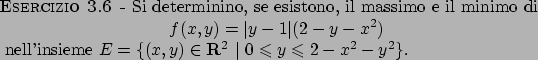

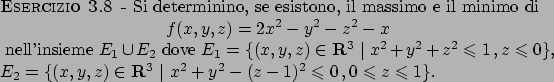


Massimi e minimi su compatti osservando le curve di livello



Massimi e minimi su illimitati e natura dei punti critici
Per studiare la natura di un punto critico di una funzione
(nel caso tale funzione sia di classe 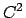 )
si può studiare la matrice hessiana in quel punto.
Per una generica matrice simmetrica
)
si può studiare la matrice hessiana in quel punto.
Per una generica matrice simmetrica  valgono le seguenti disuguaglianze
(si veda l'ESERCIZIO 3.10)
valgono le seguenti disuguaglianze
(si veda l'ESERCIZIO 3.10)
dove 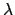 e
e 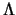 sono rispettivamente il minimo e il massimo autovalore di
sono rispettivamente il minimo e il massimo autovalore di  .
.
Ora se
 è di classe
è di classe 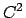 ,
, 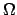 aperto di
aperto di 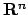 ,
,
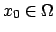 e,
denotata con
e,
denotata con  la matrice hessiana di
la matrice hessiana di  valutata in
valutata in 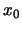 , si ha che tutti gli autovalori
di
, si ha che tutti gli autovalori
di  sono positivi (in particolare
sono positivi (in particolare  ) si ha che
) si ha che
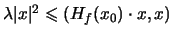 , cioè
, cioè  è definita positiva, e quindi
è definita positiva, e quindi
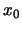 è un punto di minimo locale. Viceversa, se tutti gli autovalori sono negativi
(in particolare
è un punto di minimo locale. Viceversa, se tutti gli autovalori sono negativi
(in particolare 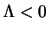 ) da
) da
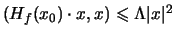 ricaviamo che
ricaviamo che
 è definita negativa e in particolare
è definita negativa e in particolare 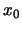 è punto di massimo locale.
è punto di massimo locale.
Un altro caso favorevole è quando la matrice  ammette un autovalore positivo ed uno negativo:
infatti restringendo la funzione agli autospazi relativi a tali autovalori si trova che tali restrizioni
ammettono rispettivamente minimo e massimo (si veda ad esempio l'ESERCIZIO 3.16).
Da ciò si conclude che il punto è di sella (cioè non è né di minimo, né di massimo).
ammette un autovalore positivo ed uno negativo:
infatti restringendo la funzione agli autospazi relativi a tali autovalori si trova che tali restrizioni
ammettono rispettivamente minimo e massimo (si veda ad esempio l'ESERCIZIO 3.16).
Da ciò si conclude che il punto è di sella (cioè non è né di minimo, né di massimo).
Per fare ciò ci si può aiutare con lo studio dei minori principali, oppure ricordando che il determinante
e la traccia di una matrice sono invarianti rispetto a trasformazioni che rendono diagonale la matrice,
per cui il determinante è il prodotto degli autovalori, la traccia la somma delgi autovalori.
Ma che succede se il determinante della matrice hessiana è nullo? Come per una funzione di una variabile si
potrebbero studiare le derivate di ordine successivo, ma nel caso di funzioni di 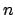 variabili si hanno applicazioni
variabili si hanno applicazioni 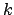 -lineari da
-lineari da
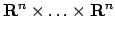 (
(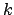 volte) in
volte) in 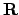 , dove
, dove 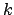 è l'ordine di
derivazione (il gradiente va da
è l'ordine di
derivazione (il gradiente va da 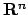 in
in 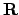 , la matrice hessiana da
, la matrice hessiana da
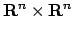 in
in  e così via). Questo rende di fatto impossibile lo studio delle derivate
successive.
e così via). Questo rende di fatto impossibile lo studio delle derivate
successive.
Fintanto che, anche se un autovalore è nullo, ne troviamo uno positivo ed uno negativo, possiamo comunque
concludere (si veda l'ESERCIZIO 3.19) che il punto è di sella.
Se invece gli autovalori sono tutti maggiori o uguali a zero, oppure tutti minori o uguali a zero,
la cosa è più complicata. Per capire il comportamento della funzione ci si può restringere
a rette (ad esempio, se un autovalore è nullo, si può studiare la restrizione della funzione
al nucleo della matrice  , come ad esempio fatto nell'ESERCIZIO 3.18),
ma ciò non e`, o può non essere sufficiente!
(si veda a tal proposito lESERCIZIO 3.20).
, come ad esempio fatto nell'ESERCIZIO 3.18),
ma ciò non e`, o può non essere sufficiente!
(si veda a tal proposito lESERCIZIO 3.20).


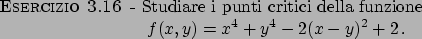

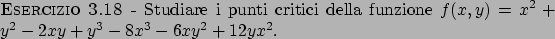

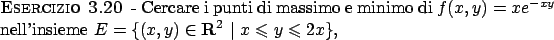
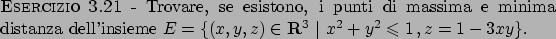

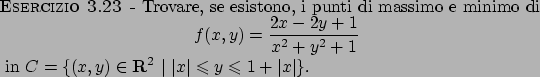
Metodo dei moltiplicatori di Lagrange


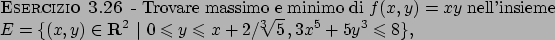
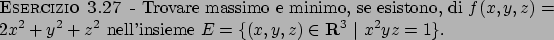

Soluzioni
Soluzione 3.1 -
Per il teorema di Weierstrass  ammette sia massimo che minimo.
All'interno si ha
ammette sia massimo che minimo.
All'interno si ha
che ha soluzione solo per 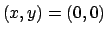 che è all'interno di
che è all'interno di  .
.
Figura 3.1:
 |
Vediamo il bordo. Prendiamo in considerazione il lato  :
parametrizziamo con la seguente funzione
:
parametrizziamo con la seguente funzione
e consideriamo
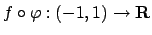 . Si ha
. Si ha
per 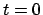 che corrisponde al punto
che corrisponde al punto
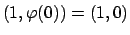 .
Chiaramente in casi semplici come questo
si può considerare direttamente la funzione
.
Chiaramente in casi semplici come questo
si può considerare direttamente la funzione  ristretta all'insieme
ristretta all'insieme
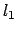 e derivare rispetto a
e derivare rispetto a 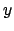 la funzione
la funzione
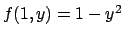 , ma in tal caso
si presti molta attenzione! Bisogna sempre ricordare che alla base c'è una
parametrizzazione e quindi non si possono sostituire le variabili con leggerezza
(si veda un esempio in cui si può cadere in inganno
nell'ESERCIZIO 3.5).
, ma in tal caso
si presti molta attenzione! Bisogna sempre ricordare che alla base c'è una
parametrizzazione e quindi non si possono sostituire le variabili con leggerezza
(si veda un esempio in cui si può cadere in inganno
nell'ESERCIZIO 3.5).
Analogamente si parametrizzano gli altri lati e derivando si ottengono i punti
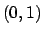 sul lato
sul lato 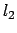 ,
,  sul lato
sul lato 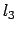 ,
, 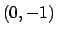 sul lato
sul lato 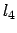 .
Abbiamo quindi i seguenti candidati:
.
Abbiamo quindi i seguenti candidati:
A questo punto valutando la funzione  su tutti e nove i punti si trova che
il punto di massimo è
su tutti e nove i punti si trova che
il punto di massimo è 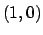 e il valore massimo di
e il valore massimo di  è
è 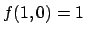 , i punti di minimo sono
, i punti di minimo sono
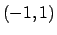 e
e 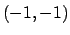 e il valore minimo di
e il valore minimo di  è
è
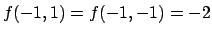 .
.
Soluzione 3.2 -
Come nell'esercizio precedente si ottiene solamente il punto 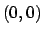 stazionario per
stazionario per
 .
.
Figura 3.2:
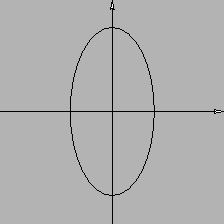 |
Vediamo il bordo: lo si può parametrizzare con la funzione
con
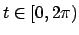 (in questo caso
non è importante l'intervallo che si sceglie, si potrebbe
considerare un qualunque intervallo
(in questo caso
non è importante l'intervallo che si sceglie, si potrebbe
considerare un qualunque intervallo 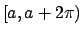 , quindi se anche
, quindi se anche 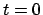 fosse
punto critico per
fosse
punto critico per
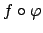 non va scartato perché cambiando l'intervallo di
definizione di
non va scartato perché cambiando l'intervallo di
definizione di 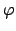 lo si può forzare ad essere un punto interno!!).
lo si può forzare ad essere un punto interno!!).
Deriviamo allora
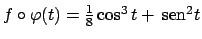 e otteniamo
e otteniamo
che si annulla se
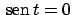 ,
, 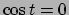 oppure
oppure
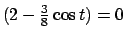 . Quest'ultmia non è mai
. Quest'ultmia non è mai 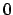 per cui
rimangono i valori
per cui
rimangono i valori
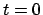 corrispondente a
corrispondente a 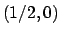 ,
, 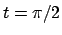 corrispondente a
corrispondente a 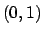 ,
,
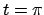 corrispondente a
corrispondente a 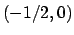 ,
, 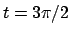 corrispondente a
corrispondente a 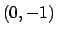 .
Si conlude valutando
.
Si conlude valutando  in questi quattro punti e nell'origine per ottenere che
in questi quattro punti e nell'origine per ottenere che
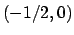 è il punto di minimo (
è il punto di minimo ( il valore minimo),
il valore minimo),
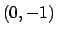 e
e 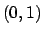 i punti di massimo (
i punti di massimo (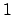 il valore massimo).
il valore massimo).
Per esercizio studiare il bordo con il metodo dei moltiplicatori di Lagrange.
Soluzione 3.3 -
L'insieme 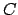 è quello rappresentato nella Figura
3.3.
Il gradiente all'interno non si annulla mai (non si annulla mai da nessuna parte).
Vediamo sul bordo. Cominciando parametrizzando la parte
di cono descritta da
è quello rappresentato nella Figura
3.3.
Il gradiente all'interno non si annulla mai (non si annulla mai da nessuna parte).
Vediamo sul bordo. Cominciando parametrizzando la parte
di cono descritta da 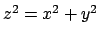 .
Si può considerare una funzione
.
Si può considerare una funzione
dove
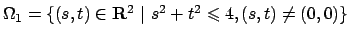 .
Il punto
.
Il punto  non viene considerato perché non è possibile
trovare una funzione differenziabile da un aperto di
non viene considerato perché non è possibile
trovare una funzione differenziabile da un aperto di  alla porzione di cono
con il vertice del nostro caso.
alla porzione di cono
con il vertice del nostro caso.
Figura 3.3:
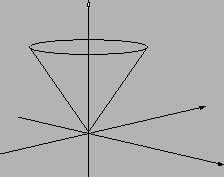 |
Allora la funzione
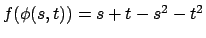 ha derivate parziali
ha derivate parziali
che si annullano per
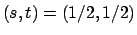 , punto che corrisponde
a
, punto che corrisponde
a
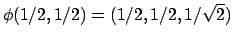 .
Ora parametrizziamo il cerchio: considero
la funzione
.
Ora parametrizziamo il cerchio: considero
la funzione
 ,
,
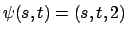 dove
dove
 .
La funzione
.
La funzione
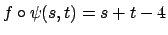 non ha mai gradiente nullo.
Ora passiamo alla circonferenza rappresentata dall'intersezione di
non ha mai gradiente nullo.
Ora passiamo alla circonferenza rappresentata dall'intersezione di
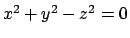 e
e 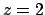 .
La parametrizzo con
.
La parametrizzo con
e ottengo che
che si annulla quando
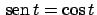 , cioè per
, cioè per 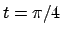 e
e 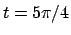 che
corrispondono ai due punti
che
corrispondono ai due punti
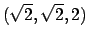 e
e
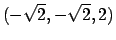 .
Conclusione: testo la funzione nei punti
.
Conclusione: testo la funzione nei punti
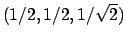 ,
,
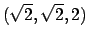 ,
,
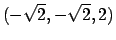 e
e 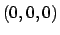 che è un vertice.
Il massimo è
che è un vertice.
Il massimo è 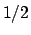 assunto nel punto
assunto nel punto
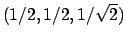 ,
il minimo
,
il minimo
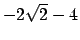 assunto nel punto
assunto nel punto
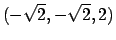 .
.
Soluzione 3.4 -
Risolviamo l'esercizio in diversi modi. Prima di tutto trasformiamo il problema:
la distanza di un generico punto in 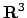 dall'origine è data da
dall'origine è data da
Chiaramente minimizzare e massimizzare su un compatto questa funzione oppure
il suo quadrato, cioè 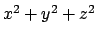 , è equivalente
(per convincersi della cosa si cominci a pensare in dimensione
, è equivalente
(per convincersi della cosa si cominci a pensare in dimensione 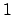 alla funzione
alla funzione
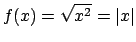 e
e 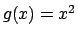 ). Per cui è più conveniente
utilizzare la funzione
). Per cui è più conveniente
utilizzare la funzione
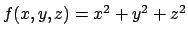 che è più semplice da
derivare e regolare in ogni punto (mentre la funzione distanza sopra non è
differenziabile nell'origine). L'insieme
che è più semplice da
derivare e regolare in ogni punto (mentre la funzione distanza sopra non è
differenziabile nell'origine). L'insieme  è dato dall'intersezione
di un cilindro lungo l'asse
è dato dall'intersezione
di un cilindro lungo l'asse 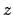 a base ellittica e il piano di equazione
a base ellittica e il piano di equazione
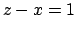 . Per cui si studia la funzione
. Per cui si studia la funzione
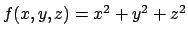 su
su 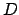 .
La funzione
.
La funzione
 è continua e
è continua e 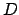 è compatto per cui ammette sia massimo che minimo.
è compatto per cui ammette sia massimo che minimo.
Il piano 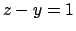 può essere visto come un grafico (
può essere visto come un grafico (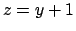 )
e quindi la parametrizzazione più semplice risulta
)
e quindi la parametrizzazione più semplice risulta
dove
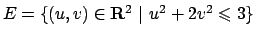 .
Definiamo la funzione
.
Definiamo la funzione
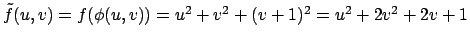 .
Annullando le derivate parziali si ottiene
.
Annullando le derivate parziali si ottiene
per cui l'unico punto stazionario è 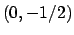 che appartiene ad
che appartiene ad  e che
corrisponde al punto
e che
corrisponde al punto
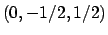 dell'insieme
dell'insieme 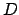 .
Sul bordo parametrizzato con
.
Sul bordo parametrizzato con
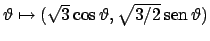 la funzione diventa
la funzione diventa
la cui derivata si annulla per
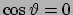 , cioè per
, cioè per
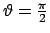 ,
,
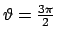 che corrispondono
ai punti
che corrispondono
ai punti
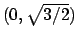 e
e
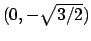 dell'insieme
dell'insieme  e ai punti
e ai punti
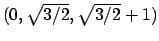 ,
,
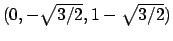 dell'insieme
dell'insieme 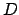 .
Valutando la funzione nei tre punti ottenuti si ha
.
Valutando la funzione nei tre punti ottenuti si ha
per cui il punto
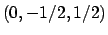 di
di 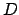 , che corrisponde a
, che corrisponde a
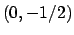 di
di  , è il punto di minima distanza dall'origine,
il punto
, è il punto di minima distanza dall'origine,
il punto
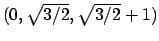 di
di 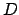 , che corrisponde a
, che corrisponde a
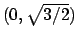 di
di  , è il punto di massima distanza dall'origine.
, è il punto di massima distanza dall'origine.
Si sarebbe potuto studiare il punto interno valutando la matrice hessiana:
che è definita positiva, per cui 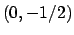 è di minimo (locale, ma a posteriori
anche assoluto).
è di minimo (locale, ma a posteriori
anche assoluto).
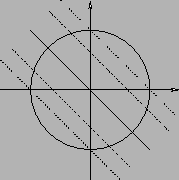
Vediamo studiando le curve di livello di 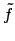 come si può risolvere il
problema. La quantità
come si può risolvere il
problema. La quantità
può essere riscritta
per cui risolvere
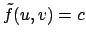 con
con 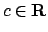 ,
cioè trovare l'insieme di livello
,
cioè trovare l'insieme di livello 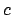 della funzione
della funzione 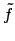 ,
è equivalente a risolvere
,
è equivalente a risolvere
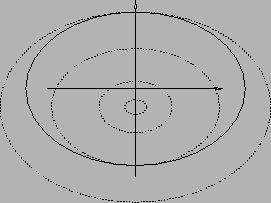
che sono ellissi, come le curve tratteggiate in Figura 3.4
(l'ellisse in neretto rappresenta il bordo di  ).
Per
).
Per 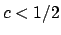 l'insieme di livello
l'insieme di livello 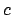 è l'insieme vuoto.
è l'insieme vuoto.
Figura 3.4:
 |
Soluzione 3.5 -
L'insieme in questione è un cilindro infinito, in particolare non è compatto, quindi non è detto
che il minimo e il massimo esistano.
Le tre derivate parziali poste uguali a zero
che forniscono solo il punto 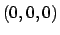 interno ad
interno ad  .
All'infinito (per
.
All'infinito (per
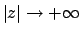 ) la funzione tende a
) la funzione tende a 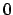 , ma è facile vedere che la funzione
assume sia valori positivi che negativi. Vediamo sul bordo:
dobbiamo parametrizzare la superficie
, ma è facile vedere che la funzione
assume sia valori positivi che negativi. Vediamo sul bordo:
dobbiamo parametrizzare la superficie
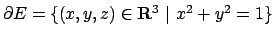 .
.
!!! Si può essere tentati dall'inserire nell'espressione di  la quantità
la quantità 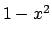 al posto di
al posto di 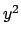 e considerare così
e considerare così
Questo corrisponde a considerare le due parametrizzazioni
Annullando le derivate di 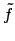 si ottengono le soluzioni
si ottengono le soluzioni 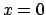 e
e 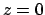 che corrispondono ai due punti
che corrispondono ai due punti 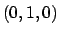 e
e 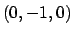 (che risultano i punti di massimo per la funzione
(che risultano i punti di massimo per la funzione  ).
A questo punto però vanno anche considerati gli estremi
).
A questo punto però vanno anche considerati gli estremi 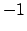 e
e 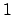 del dominio
di
del dominio
di 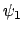 e
e 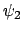 che corrispondono ai punti
che corrispondono ai punti
nei quali va valutata poi  .
Se si considera la quantità
.
Se si considera la quantità 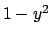 al posto di
al posto di 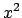 si stanno
considerando le due parametrizzazioni
si stanno
considerando le due parametrizzazioni
si considera
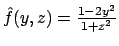 e annullando le derivate
si trovano i due punti
e annullando le derivate
si trovano i due punti 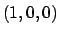 e
e 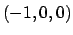 ai quali vanno aggiunti
i punti corrispondenti agli estremi
ai quali vanno aggiunti
i punti corrispondenti agli estremi
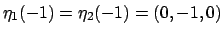 e
e
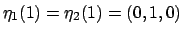 .
.
Se parametrizziamo la superficie con
e consideriamo
derivando si ottengono
per cui si hanno le soluzioni
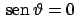 o
o
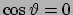 e
e 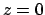 ,
che corrispondono ai punti
quattro
,
che corrispondono ai punti
quattro 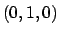 ,
, 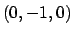 ,
, 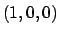 e
e 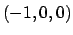 , due di massimo, due di minimo.
, due di massimo, due di minimo.
Perché in questo modo abbiamo trovato quattro punti, mentre per 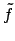 e
e
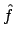 solamente due?
solamente due?
Soluzione 3.9 -
L'insieme  , in Figura 3.5,
non è compatto, quindi l'esistenza del massimo e del minimo non è garantita.
Annullando le derivate si ottiene il punto critico
, in Figura 3.5,
non è compatto, quindi l'esistenza del massimo e del minimo non è garantita.
Annullando le derivate si ottiene il punto critico 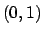 .
Si vede facilmente che
.
Si vede facilmente che
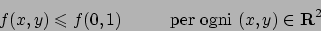 |
(3.1) |
(studiare l'hessiana per esercizio).
Figura 3.5:
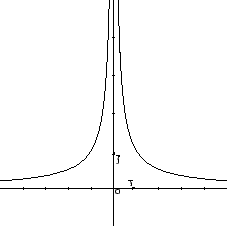 |
All'infinito: poiché
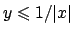 si ha che
si ha che
 quindi
quindi
Se si considera quindi il limite per
 in
in  si hanno due
possibilità: o
si hanno due
possibilità: o
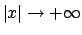 (e
(e 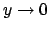 ) oppure
) oppure
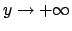 (e in questo caso
(e in questo caso 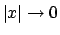 ). Nel primo dei due casi dalla stima di sopra si ottiene
che
). Nel primo dei due casi dalla stima di sopra si ottiene
che 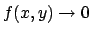 . Nel secondo caso possiamo stimare la
. Nel secondo caso possiamo stimare la  come segue,
visto che
come segue,
visto che
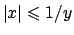 :
:
Conlcusione:
(in realtà
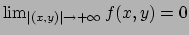 ! mostrarlo per esercizio).
Poiché
! mostrarlo per esercizio).
Poiché  è sempre positiva, il limite all'infinito è zero e inoltre dalla stima
(3.1) si conclude che la funzione ha un punto di massimo assoluto in
è sempre positiva, il limite all'infinito è zero e inoltre dalla stima
(3.1) si conclude che la funzione ha un punto di massimo assoluto in 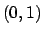 e non ha minimo.
e non ha minimo.
Soluzione 3.10 -
Derivando la funzione  rispetto a
rispetto a  si ha:
si ha:
quindi
per ogni
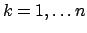 .
Di conseguenza, anullando le derivate, si ha
.
Di conseguenza, anullando le derivate, si ha
e ciò è equivalente a dire che
cioè 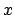 è un autovettore e
è un autovettore e 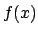 è un autovalore.
Senza bisogno di trovare le soluzioni
è un autovalore.
Senza bisogno di trovare le soluzioni 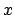 sicuramente
sicuramente 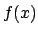 è un autovalore,
quindi il minimo valore assunto da
è un autovalore,
quindi il minimo valore assunto da  è il minimo autovalore di
è il minimo autovalore di  e il
massimo valore assunto da
e il
massimo valore assunto da  è il massimo autovalore di
è il massimo autovalore di  .
.
Volendo risolvere il problema con il metodo dei moltiplicatori di Lagrange,
si osservi innanzitutto che la funzione  può essere ridefinita sulla ipersfera
in
può essere ridefinita sulla ipersfera
in 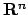
dato che
e quindi
Per cui ci si può limitare a considerare
definita in 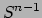 . Si consideri la funzione
. Si consideri la funzione
visto che cerchiamo i punti stazionari in 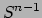 e
e 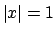 se e solo se
se e solo se 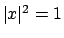 .
Le derivate forniscono (la matrice è simmetrica)
.
Le derivate forniscono (la matrice è simmetrica)
Dalle prime 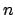 equazioni si ricava che
equazioni si ricava che
il che significa che 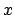 deve essere un autovettore (e
deve essere un autovettore (e 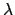 un autovalore).
I punti stazionari di
un autovalore).
I punti stazionari di 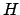 in
in  sono quindi tutte le
sono quindi tutte le 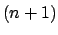 -uple
-uple
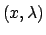 con
con 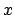 autovettore di norma
autovettore di norma 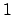 e
e 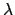 autovalore di
autovalore di  .
.
Si osservi come dalle equazioni sopra si ricava
che nel caso in cui  sia diagonale fornisce subito il fatto che gli autovalori
sono gli elementi della diagonale e gli autovettori sono del tipo
sia diagonale fornisce subito il fatto che gli autovalori
sono gli elementi della diagonale e gli autovettori sono del tipo
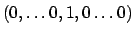 .
.
Soluzione 3.11 -
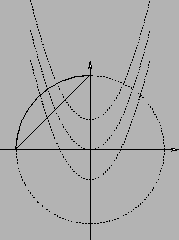
L'insieme  è quello in Figura 3.6,
quelle tratteggiate sono curve di livello
(parabole).
è quello in Figura 3.6,
quelle tratteggiate sono curve di livello
(parabole).
Figura 3.6:
 |
Risolveremo il problema senza fare calcoli, ma osservando gli insiemi di livello della
funzione (svolgere per esercizio i calcoli, anche per confronto, studiando il gardiente,
la matrice hessiana e studiando
sul bordo il comportamento della funzione come di solito).
Fissiamo 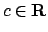 e vediamo dove
e vediamo dove 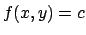 : la risposta è l'insieme
: la risposta è l'insieme 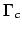 rappresentato dall'intersezione di
rappresentato dall'intersezione di  con la parabola di equazione
(si veda anche la Figura 3.6)
con la parabola di equazione
(si veda anche la Figura 3.6)
Chiaramente il valore massimo (rispettivamente il minimo)
che assume  è il massimo
è il massimo 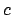 (rispettivamente il minimo
(rispettivamente il minimo 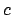 ) per cui
) per cui
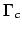 non è vuoto
(cioè il massimo
non è vuoto
(cioè il massimo 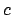 per cui la parabola
per cui la parabola
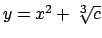 interseca l'insieme
interseca l'insieme  ).
Concludendo: il minimo sarà assunto nel vertice di
).
Concludendo: il minimo sarà assunto nel vertice di  dato dal punto
dato dal punto 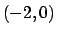 e il massimo nel vertice di
e il massimo nel vertice di  dato dal punto
dato dal punto 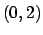 .
.
Per calcolare i valori basta valutare la funzione in questi due punti o trovare
i valori di 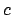 per cui le parabole passano per questi punti (farlo per esercizio!!).
Per concludere i valori minimo e massimo sono rispettivamente
per cui le parabole passano per questi punti (farlo per esercizio!!).
Per concludere i valori minimo e massimo sono rispettivamente 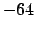 e
e 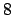 .
.
Soluzione 3.12 -
La funzione è continua su un compatto, quindi sicuramente ammette massimo e minimo.
L'insieme su cui è definita  e tre suoi insiemi di livello sono disegnati
in Figura 3.7 (le linee tratteggiate allo stesso modo
fatto parte dello stesso insieme di livello).
e tre suoi insiemi di livello sono disegnati
in Figura 3.7 (le linee tratteggiate allo stesso modo
fatto parte dello stesso insieme di livello).
Figura 3.7:
 |
Si fissi  e si denoti con
e si denoti con
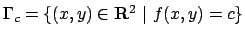 .
Chiaramente per
.
Chiaramente per 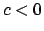 l'insieme
l'insieme  è il vuoto, per
è il vuoto, per 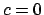 si ha che
si ha che
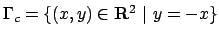 ,
per
,
per 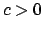
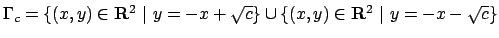 .
Per cui il minimo di
.
Per cui il minimo di  è
è 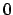 assunto in tutto l'insieme
assunto in tutto l'insieme
![$\Gamma_0 \cap E = \{ (x,y) \in {\bf R}^2 \vert y =-x , [-\sqrt{2} , \sqrt{2}]\}$](img275.png) ,
il massimo è assunto dove l'insieme di livello interseca
,
il massimo è assunto dove l'insieme di livello interseca  sul bordo
e precisamente nei punti
sul bordo
e precisamente nei punti
 e
e
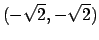 (trovare le equazioni dell rette!).
Il valore massimo è
(trovare le equazioni dell rette!).
Il valore massimo è
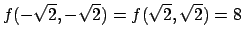 .
.
Soluzione 3.13 -
L'insieme  è una corona circolare e gli insiemi di livello sono delle ellissi
(si veda Figura 3.8), come si può facilmente ricavare ponendo
è una corona circolare e gli insiemi di livello sono delle ellissi
(si veda Figura 3.8), come si può facilmente ricavare ponendo
Figura 3.8:
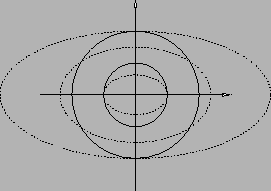 |
Minore è il valore 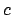 e minori sono i semiassi dell'ellisse, l'insieme sul quale
la funzione assume il valore costante
e minori sono i semiassi dell'ellisse, l'insieme sul quale
la funzione assume il valore costante 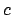 . Per cui i punti di minimo sono
. Per cui i punti di minimo sono
 e
e 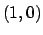 dove l'ellisse descritta da
dove l'ellisse descritta da
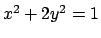 interseca la parte di
bordo di
interseca la parte di
bordo di  data dal cerchio di raggio
data dal cerchio di raggio 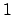 (quindi il valore minimo è
(quindi il valore minimo è 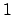 ),
i punti di massimo sono
),
i punti di massimo sono 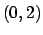 e
e 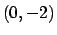 dove l'ellisse descritta da
dove l'ellisse descritta da
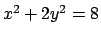 interseca la parte di
bordo di
interseca la parte di
bordo di  data dal cerchio di raggio
data dal cerchio di raggio 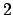 (quindi il valore minimo è
(quindi il valore minimo è 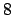 ).
).
Soluzione 3.14 -
La funzione
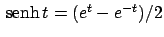 è strettamente
crescente per cui i punti critici, e la loro natura, sono gli stessi per la funzione
è strettamente
crescente per cui i punti critici, e la loro natura, sono gli stessi per la funzione
Attenzione: a questo punto è possibile studiare la funzione 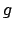 anziché
anziché
 perché
perché
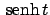 è strettamente crescente e
quindi la sua derivata è sempre diversa da zero, se fosse solamente crescente
(non decrescente)
ciò non sarebbe possibile. Un'altra cosa: se si avesse una funzione strettamente
decrescente il ragionamento può essere applicato comunque, con l'attenzione che
la natura dei punti viene mutata, un punto di massimo per
è strettamente crescente e
quindi la sua derivata è sempre diversa da zero, se fosse solamente crescente
(non decrescente)
ciò non sarebbe possibile. Un'altra cosa: se si avesse una funzione strettamente
decrescente il ragionamento può essere applicato comunque, con l'attenzione che
la natura dei punti viene mutata, un punto di massimo per 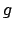 sarebbe un minimo
per
sarebbe un minimo
per  e viceversa.
e viceversa.
Vediamo ora di capire com'è fatto l'insieme  .
La disequazione
.
La disequazione
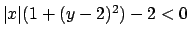 è equivalente a
è equivalente a
per cui l'insieme  è un insieme illimitato come quello in
Figura 3.9. Per ricavarlo si noti che la diseguaglianza denota la
è un insieme illimitato come quello in
Figura 3.9. Per ricavarlo si noti che la diseguaglianza denota la
Figura 3.9:
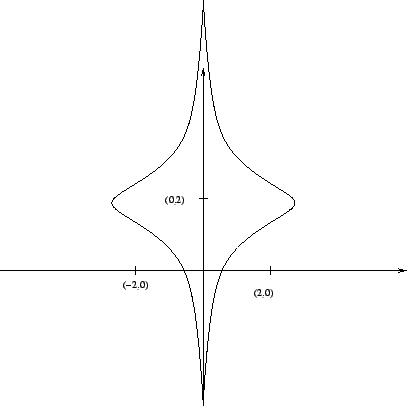 |
parte interna alle due curve di equazione
 e
e
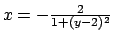 .
.
Veniamo ai conti: posto il gradiente di 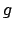 uguale a
uguale a 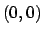 si trovano i punti
si trovano i punti
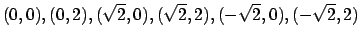 .
Attenzione: i punti
.
Attenzione: i punti
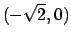 e
e 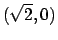 non appartengono ad
non appartengono ad  , per
cui non ci interessano.
, per
cui non ci interessano.
Calcolando le derivate seconde si ottiene che la matrice hessiana è
Questo è il caso più fortunato: la matrice è diagonale per cui conosciamo già
gli autovalori il cui segno ci fornisce le informazioni sulla natura dei punti:
La funzione  ammette massimo e minimo su
ammette massimo e minimo su 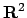 ? (assoluti). NO! Infatti
? (assoluti). NO! Infatti
per cui poiché il seno iperbolico va a  a
a  e a
e a 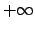 a
a 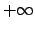 anche
anche  risulta illimitata sia dal basso che dall'alto.
risulta illimitata sia dal basso che dall'alto.
Soluzione 3.15 -
Annullando il gradiente si arriva alle equazioni
da cui
per cui le soluzioni sono
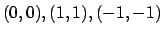 .
La matrice hessiana è
.
La matrice hessiana è
Consideriamo il punto 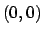 :
:
Valutiamo il segno degli autovalori: anche se
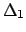 , il determinante del minore principale
, il determinante del minore principale 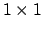 (di fatto il termine
(di fatto il termine
![$[H_f(0,0)]_{11}$](img308.png) della matrice) è nullo, si ha che
della matrice) è nullo, si ha che
 è anche il determinante della matrice nonché il prodotto degli
autovalori: ne deduciamo che necessariamente uno è positivo e l'altro negativo
per cui
è anche il determinante della matrice nonché il prodotto degli
autovalori: ne deduciamo che necessariamente uno è positivo e l'altro negativo
per cui 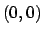 è di sella.
è di sella.
Per quanto riguarda il punto 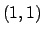 si ha che
si ha che
che si può verificare essere definita positiva, per cui 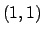 è di minimo locale.
Si può calcolare anche il determinante che è positivo, da cui si deduce
che il prodotto dei due autovalori è positivo (
è di minimo locale.
Si può calcolare anche il determinante che è positivo, da cui si deduce
che il prodotto dei due autovalori è positivo (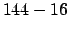 ), per cui si potrebbero
avere due autovalori positivi o due negativi. Ma un altro invariante è la traccia,
la somma degli elementi sulla diagonale, che è anche la somma degli autovalori.
La traccia è
), per cui si potrebbero
avere due autovalori positivi o due negativi. Ma un altro invariante è la traccia,
la somma degli elementi sulla diagonale, che è anche la somma degli autovalori.
La traccia è 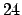 per cui se la somma degli autovalori è positiva deduciamo che
il segno dei due autovalori non può essere altro che positivo.
Lo stesso vale per il punto
per cui se la somma degli autovalori è positiva deduciamo che
il segno dei due autovalori non può essere altro che positivo.
Lo stesso vale per il punto 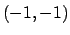 .
.
Per concludere si vede che
per cui la funzione non ammette massimo e ammette due punti di minimo assoluto.
Soluzione 3.16 -
Anullando il gradiente si ottiene
Dalla prima equazione si ricava che 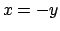 e quindi dalla seconda
e quindi dalla seconda
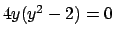 . Per cui le soluzioni sono
. Per cui le soluzioni sono 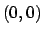 ,
,
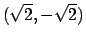 ,
,
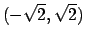 . La matrice hessiana è
. La matrice hessiana è
Si ha che
che è definita positiva, per cui i due punti sono di minimo locale, ma
ha determinante 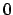 e quindi almeno uno dei due autovalori è
e quindi almeno uno dei due autovalori è 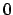 (la traccia in
questo caso non aiuta).
Come fare per stabilire la natura del punto
(la traccia in
questo caso non aiuta).
Come fare per stabilire la natura del punto 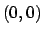 ?
Un modo possibile è studiare il segno di
?
Un modo possibile è studiare il segno di  per capire se il punto in questione
è di sella: si osservi che
per capire se il punto in questione
è di sella: si osservi che
e quindi 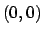 risulta di minimo per
risulta di minimo per  ristretta alla retta
ristretta alla retta 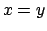 , mentre
risulta di massimo per
, mentre
risulta di massimo per  ristretta alla retta
ristretta alla retta 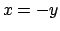 . Infatti
. Infatti
che ha un massimo in 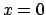 (
(
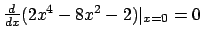 ,
,
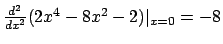 ).
Si conclude che
).
Si conclude che 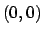 è un punto di sella per
è un punto di sella per  .
.
Soluzione 3.17 -
Al solito si calcolino le derivate parziali e le si annullino. Si ottiene
da cui si ottengono i punti 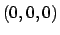 e
e 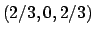 . La matrice hessiana è data
da
. La matrice hessiana è data
da
Si ha
Valutando i determinanti dei minori pricipali: 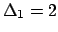 ,
,
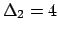 ,
, 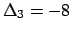 . La matrice non è definita positiva e
il prodotto degli autovalori (
. La matrice non è definita positiva e
il prodotto degli autovalori (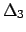 ) è negativo: gli autovalori potrebbero
essere tutti negativi oppure due positivi e uno negativo. Ma
) è negativo: gli autovalori potrebbero
essere tutti negativi oppure due positivi e uno negativo. Ma 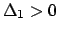 e
e
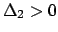 , per cui due autovalori sono positivi
(un altro invariante è la traccia della matrice, ossia la somma degli elementi
sulla diagonale che corrisponde alla somma degli autovalori: poiché la somma è
, per cui due autovalori sono positivi
(un altro invariante è la traccia della matrice, ossia la somma degli elementi
sulla diagonale che corrisponde alla somma degli autovalori: poiché la somma è
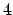 anche da ciò si può dedurre che i tre autovalori non possono essere tutti
negativi). Conclusione:
anche da ciò si può dedurre che i tre autovalori non possono essere tutti
negativi). Conclusione: 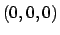 non è né di massimo, né di minimo.
non è né di massimo, né di minimo.
i cui minori hanno determinanti 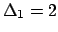 ,
,
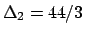 ,
,
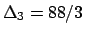 , per cui il punto
, per cui il punto 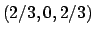 è di minimo locale.
è di minimo locale.
Soluzione 3.18 -
Le derivate prime di  sono
sono
che si annullano in 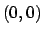 , unico punto critico.
Studiamo le derivate seconde.
La matrice hessiana in
, unico punto critico.
Studiamo le derivate seconde.
La matrice hessiana in 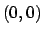 è
è
che ha determinante nullo: almeno uno dei due autovalori è nullo. In realtà solo
uno visto che la traccia è positiva, ma questo non ci aiuta a capire
la natura del punto. Gli autovalori dovrebbero essere 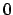 e
e 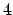 dato che il determinante
è
dato che il determinante
è 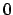 e la traccia
e la traccia 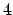 , ma in dimensione più alta non è possibile determinare gli
autovalori in questo modo (se conosco la somma e il prodotto di
, ma in dimensione più alta non è possibile determinare gli
autovalori in questo modo (se conosco la somma e il prodotto di 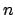 numeri posso
determinare gli
numeri posso
determinare gli 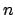 numeri solo se
numeri solo se 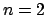 ).
Calcoliamo allora il polinomio caratteristico e le sue radici:
).
Calcoliamo allora il polinomio caratteristico e le sue radici:
Le radici effettivamente sono 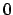 e
e 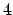 . Gli autospazi: relativamente a
. Gli autospazi: relativamente a 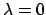 si ha
si ha
che fornisce la retta 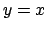 .
L'altro non è importante calcolarlo, l'autovalore è
positivo e la funzione ristretta all'autospazio relativo all'autovalore
.
L'altro non è importante calcolarlo, l'autovalore è
positivo e la funzione ristretta all'autospazio relativo all'autovalore 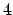 sarà
convessa (farlo per esercizio!).
Bisogna capire che succede restringendo la funzione alla retta
sarà
convessa (farlo per esercizio!).
Bisogna capire che succede restringendo la funzione alla retta 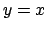 :
valutiamo
:
valutiamo
che non è convessa, per cui il punto  non è di minimo. Se la funzione fosse
più complicata si studia derivando per
non è di minimo. Se la funzione fosse
più complicata si studia derivando per 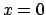 la funzione
la funzione 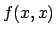 (farlo per esercizio: la derivata prima è zero, la seconda pure, la terza finalmente
è
(farlo per esercizio: la derivata prima è zero, la seconda pure, la terza finalmente
è 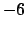 il che implica che
il che implica che 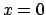 è un flesso).
è un flesso).
Soluzione 3.19 -
Derivando  si ottiene che l'unico punto critico è
si ottiene che l'unico punto critico è 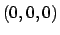 . La matrice hessiana
in quel punto è data da
. La matrice hessiana
in quel punto è data da
che ha determinante nullo, per cui almeno uno degli autovalori è nullo,
e traccia positiva, per cui non conosciamo il segno degli due autovalori
(potrebbero essere tutti e due positivi oppure uno positivo e l'altro nullo, non
entrambi negativi). Il polinomio caratteristico è dato da
che si annulla per 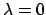 e per le soluzioni di
e per le soluzioni di
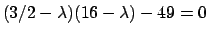 . Risolvendo si ottengono due soluzioni, una positiva e una
negativa (si osservi come tutte le entrate della matrice siano positive anche se un
autovalore è negativo).
Concludiamo che lungo una direzione la funzione è concava, ungo un'altra è convessa
e non c'è bisogno di verificare lungo l'autospazio relativo all'autovalore nullo
il comportamento della funzione.
. Risolvendo si ottengono due soluzioni, una positiva e una
negativa (si osservi come tutte le entrate della matrice siano positive anche se un
autovalore è negativo).
Concludiamo che lungo una direzione la funzione è concava, ungo un'altra è convessa
e non c'è bisogno di verificare lungo l'autospazio relativo all'autovalore nullo
il comportamento della funzione.
Soluzione 3.20 -
Dai conti si ricava che 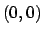 l'unico punto critico e che la matrice hessiana di
l'unico punto critico e che la matrice hessiana di  in
in 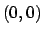 è la matrice
è la matrice
Se proviamo a restringere  lungo la retta
lungo la retta 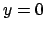 , nucleo della matrice,
troviamo che tale restrizione ammette
minimo in
, nucleo della matrice,
troviamo che tale restrizione ammette
minimo in 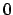 . Poiché l'altro autovalore è positivo si potrebbe essere tenati di conludere
che tale punto è di minimo.
Se restringiamo
. Poiché l'altro autovalore è positivo si potrebbe essere tenati di conludere
che tale punto è di minimo.
Se restringiamo  a tutte le rette per l'origine troviamo ancora che tali restrizioni ammettono minimo
nell'origine. Ma ciò non basta. Infatti la funzione è chiaramente positiva se
a tutte le rette per l'origine troviamo ancora che tali restrizioni ammettono minimo
nell'origine. Ma ciò non basta. Infatti la funzione è chiaramente positiva se  e per
e per
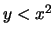 (è il prodotto di due quantità che hanno lo stesso segno), ma per
(è il prodotto di due quantità che hanno lo stesso segno), ma per
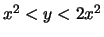 le due quantità
le due quantità  e
e 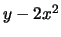 hanno segno discorde, per cui in tale regione la funzione
è negativa. Per concludereSi annulla lungo le due curve
hanno segno discorde, per cui in tale regione la funzione
è negativa. Per concludereSi annulla lungo le due curve 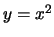 e
e 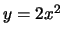 . Per cui in qualunque intorno
dell'origine
. Per cui in qualunque intorno
dell'origine  assume valori sia positivi che negativi e si annulla nell'origine.
Di conseguenza il punto è di sella, anche se la restrizione a tutte le rette ammette minimo nell'origine.
assume valori sia positivi che negativi e si annulla nell'origine.
Di conseguenza il punto è di sella, anche se la restrizione a tutte le rette ammette minimo nell'origine.
Soluzione 3.21 -
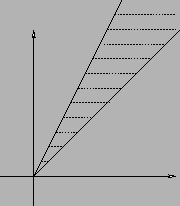
L'insieme  è illimitato (quello tratteggiato in Figura 3.10)
e le derivate parziali non si annullano mai contemporaneamente su
è illimitato (quello tratteggiato in Figura 3.10)
e le derivate parziali non si annullano mai contemporaneamente su  . Infatti
. Infatti
e la derivata rispetto a 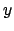 non è mai zero all'interno di
non è mai zero all'interno di  !
!
Figura 3.10:
 |
Vediamo sul bordo: parametrizzando il bordo con le curve
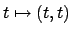 e
e
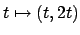 con
con
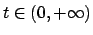 si ottiene prima
si ottiene prima
che si annulla per
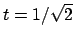 che corrisponde al punto
che corrisponde al punto
 , poi
, poi
che si annulla per 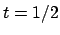 , che corrisponde al punto
, che corrisponde al punto 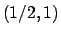 .
Vediamo all'infinito: poiché in
.
Vediamo all'infinito: poiché in 
si ha che
per cui
Esaminiamo i candidati, i due punti trovati e il vertice:
Soluzione 3.22 -
I punti
 e
e
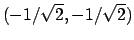 sono di minima distanza,
sono di minima distanza,
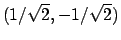 e
e
 di massima.
di massima.
Soluzione 3.23 -
Traccia -
Il vincolo può essere visto come grafico per cui una delle parametrizzazioni possibili e più
semplici è
(ma anche
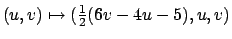 e
e
 vanno bene). Ci si riduce così
ad una funzione di due variabili
vanno bene). Ci si riduce così
ad una funzione di due variabili
Soluzione 3.25 -
Usando il metodo dei moltiplicatori di Lagrange consideriamo la funzione
La derivata parziale rispetto a 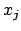 di
di  è
è
 , quindi
, quindi
da cui si deduce che 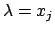 per
per
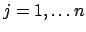 . Si noti che non è
necessario risolvere il sistema per concludere perché il valore di
. Si noti che non è
necessario risolvere il sistema per concludere perché il valore di 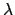 non è indispensabile. Per cui si deduce che la soluzione (l'unica)
del sistema è tale che
non è indispensabile. Per cui si deduce che la soluzione (l'unica)
del sistema è tale che
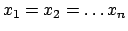 (che sarà uguale anche al
valore di
(che sarà uguale anche al
valore di 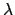 , ma non è importante).
Se tutti i valori devono essere uguali e il loro prodotto è
, ma non è importante).
Se tutti i valori devono essere uguali e il loro prodotto è 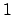 si ha
necessariamente
si ha
necessariamente
Per vedere che questo è un punto di minimo per la somma usiamo l'induzione:
mostriamo che
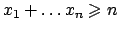 ogni volta che
ogni volta che
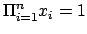 .
.
Se 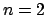 : dobbiamo vedere che
: dobbiamo vedere che
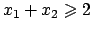 sapendo che
sapendo che
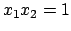 . Per esercizio mostrare (derivando) che la funzione, definita
per
. Per esercizio mostrare (derivando) che la funzione, definita
per 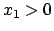 , soddisfa
, soddisfa
Supponiamo quindi che l'affermazione sia vera per 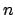 e mostriamola per
e mostriamola per 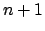 .
Siano quindi
.
Siano quindi 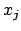 ,
,
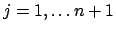 ,
, 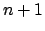 numeri tali che
numeri tali che
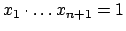 . È chiaro che se questi numeri non sono tutti
uguali a
. È chiaro che se questi numeri non sono tutti
uguali a 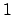 (e avremmo concluso) ne esiste uno minore di uno e uno maggiore.
Diciamo che siano
(e avremmo concluso) ne esiste uno minore di uno e uno maggiore.
Diciamo che siano 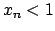 ,
, 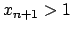 . Chiamando
. Chiamando
 si hanno
si hanno 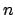 numeri
numeri
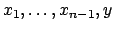 il cui prodotto è
il cui prodotto è 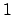 e quindi,
per l'ipotesi induttiva, sappiamo che
e quindi,
per l'ipotesi induttiva, sappiamo che
Vogliamo però mostrare che questa somma è maggiore o uguale a 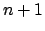 :
:
perché stiamo assumendo
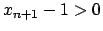 e
e 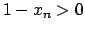 .
.
Conseguenza interessante: da questo fatto si può mostrare che
la media geometrica è minore o uguale della media aritmetica (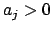 )
)
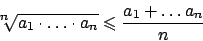 |
(3.2) |
Infatti è sufficiente considerare le quantità
il cui prodotto è 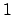 , per cui per quanto mostrato si ha
, per cui per quanto mostrato si ha
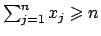 , cioè
, cioè
Soluzione 3.26 -
Il volume è dato dal prodotto delle lunghezze dei tre lati. Indicando con 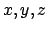 le tre lunghezze la funzione da massimizzare è allora
le tre lunghezze la funzione da massimizzare è allora
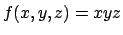 .
La superficie di ogni singola faccia è il prodotto delle lunghezze dei due lati
che la determinano, per cui il vincolo è
.
La superficie di ogni singola faccia è il prodotto delle lunghezze dei due lati
che la determinano, per cui il vincolo è
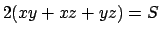 . Uso il metodo dei moltiplicatori di Lagrange:
si consideri la funzione
. Uso il metodo dei moltiplicatori di Lagrange:
si consideri la funzione
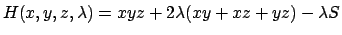 e le sue derivate parziali
e le sue derivate parziali
Dalla prima e dalla seconda equazione si ricava che
e
da cui (si ricordi che  )
) 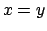 .
Analogamente dalla prima e dalla terza si ricava
.
Analogamente dalla prima e dalla terza si ricava 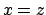 , per cui si conclude
che
, per cui si conclude
che 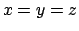 .
Questa è la soluzione, che corrisponde a dire che se c'è un parallelepipedo
di volume massimo questo deve essere un cubo.
Vediamo si stabilire quanti punti ci sono che verificano questa condizione:
si sa che
.
Questa è la soluzione, che corrisponde a dire che se c'è un parallelepipedo
di volume massimo questo deve essere un cubo.
Vediamo si stabilire quanti punti ci sono che verificano questa condizione:
si sa che
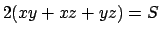 e d'altra parte che
e d'altra parte che
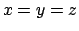 . Quindi esiste solo un punto sul vincolo dato da
. Quindi esiste solo un punto sul vincolo dato da
Il volume corrispondente a questo valore è
Vediamo in due modi
che
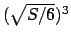 è il massimo valore possibile per il volume.
è il massimo valore possibile per il volume.
Si può utilizzare la formula (3.2). Infatti presi
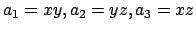 si ha da (3.2)
si ha da (3.2)
da cui
ogniqualvolta la somma
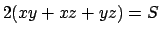 .
.
Un altro modo è il seguente: la funzione volume
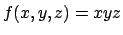 è sempre
positiva e ha un unico punto critico. Vediamo che all'infinito la funzione tende
a zero (o equivalentemente
che
è sempre
positiva e ha un unico punto critico. Vediamo che all'infinito la funzione tende
a zero (o equivalentemente
che 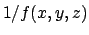 tende a
tende a 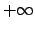 ) quando
) quando
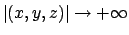 sul vincolo:
sul vincolo:
È chiaro che quando
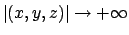 sul vincolo
sul vincolo
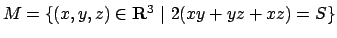 non tutte le variabili possono andare a
non tutte le variabili possono andare a 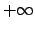 , e almeno una delle tre
deve quindi convergere a
, e almeno una delle tre
deve quindi convergere a 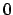 . Per cui
. Per cui
Soluzione 3.27 -
L'insieme  è quello delimitato dalle curve in Figura 3.11
e dall'asse
è quello delimitato dalle curve in Figura 3.11
e dall'asse 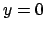 .
.
Figura 3.11:
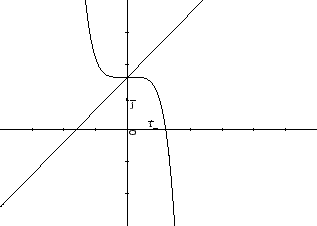 |
Infatti abbiamo le seguenti limitazioni: 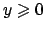 e
e
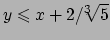 che definiscono due semipiani. La terza
che definiscono due semipiani. La terza
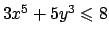 può essere vista come
può essere vista come
Le derivate parziali si annullano solo nell'origine, che non appartiene
all'interno di  , quindi va scartato. Vediamo il bordo.
Prima la parte in cui
, quindi va scartato. Vediamo il bordo.
Prima la parte in cui 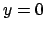 : chiaramente
: chiaramente 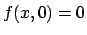 (provare ad usare i moltiplicatori). La parte di bordo che appartiene alla retta
si può parametrizzare con
(provare ad usare i moltiplicatori). La parte di bordo che appartiene alla retta
si può parametrizzare con
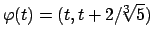 con
con
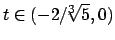 .
.
Si ottiene
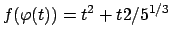 la cui derivata è
la cui derivata è
che si annulla per
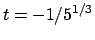 . Quindi il punto
. Quindi il punto
 è un punto candidato.
Sull'ultimo tratto di bordo usiamo il metodo dei moltiplicatori di Lagrange:
cerchiamo i punti stazionari (in
è un punto candidato.
Sull'ultimo tratto di bordo usiamo il metodo dei moltiplicatori di Lagrange:
cerchiamo i punti stazionari (in 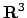 ) della funzione
) della funzione
Derivando si ottiene
Dalla prima e dalla seconda si ha che
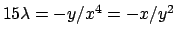 da cui
da cui
Inserendo quest'informazione nella terza equazione si ricava
Valutando  nei punti
nei punti
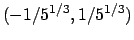 ,
, 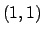 ,
, 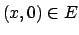 , e il
vertice
, e il
vertice
 si ottiene
si ottiene
Soluzione 3.28 -
Usando il metodo dei moltiplicatori di Lagrange, si consideri la funzione
e annullando le sue derivate si ottiene
Dalla seconda e dalla terza si ottiene
Dalla quarta equazione si ricava che 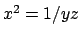 per cui
per cui 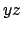 è positivo
(o sia
è positivo
(o sia 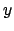 che
che 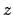 sono positivi, o entrambi sono negativi, quindi la possibilità
sono positivi, o entrambi sono negativi, quindi la possibilità
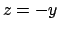 va scartata).
va scartata).
Dalla prima equazione, sfruttando 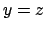 e
e 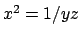 , si ha
, si ha
da cui si ricava che 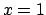 oppure
oppure 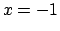 . Per cui i punti trovati sono
. Per cui i punti trovati sono
Si ha che 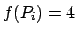 per ogni
per ogni 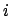 . Come fare per capire se sono massimi o minimi?
Dalla risoluzione dell'ESERCIZIO 3.25 sappiamo che
se
. Come fare per capire se sono massimi o minimi?
Dalla risoluzione dell'ESERCIZIO 3.25 sappiamo che
se 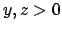 e
e 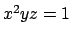 allora
allora
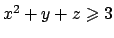 da cui
da cui
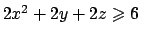 . Si ha usando
. Si ha usando
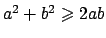
da cui
Se 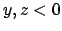 considero
considero 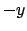 e
e 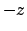 che sono positivi e il cui prodotto è sempre
che sono positivi e il cui prodotto è sempre 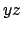 e ripeto il ragionamento. Conclusione:
e ripeto il ragionamento. Conclusione:
per cui 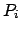 ,
, 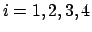 , sono tutti punti di minimo.
, sono tutti punti di minimo.
Soluzione 3.29 -
Con due vincoli considero la funzione
Si trovano i punti
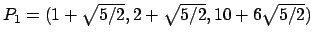 e
e
 che sono rispettivamente di minimo
e di massimo.
che sono rispettivamente di minimo
e di massimo.



Next: About this document ...
Up: 3esercizi
Previous: 3esercizi
Fabio Paronetto
2005-06-23
![]() continua in
continua in ![]() compatto di
compatto di ![]() .
ammette sia massimo che minimo.
.
ammette sia massimo che minimo.
![]() ,
, ![]() aperto di
aperto di ![]() ,
,
![]() .
Se
.
Se
![]() è un punto di minimo o di massimo per
è un punto di minimo o di massimo per ![]() allora
allora
![]() per
per ![]() .
.
![]() (in alcune situazioni):
(in alcune situazioni):
![]() è compatto (cioè limitato e chiuso):
è compatto (cioè limitato e chiuso):


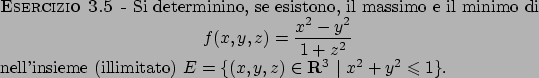
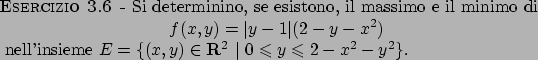

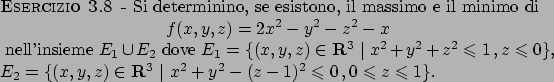


![]()
![]()
![]()
![]() )
si può studiare la matrice hessiana in quel punto.
Per una generica matrice simmetrica
)
si può studiare la matrice hessiana in quel punto.
Per una generica matrice simmetrica ![]() valgono le seguenti disuguaglianze
(si veda l'ESERCIZIO 3.10)
valgono le seguenti disuguaglianze
(si veda l'ESERCIZIO 3.10)
![]() ammette sia massimo che minimo.
All'interno si ha
ammette sia massimo che minimo.
All'interno si ha
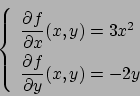
![]() :
parametrizziamo con la seguente funzione
:
parametrizziamo con la seguente funzione