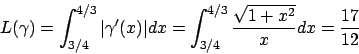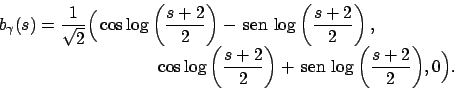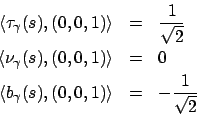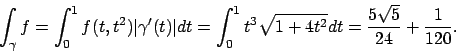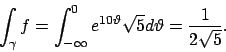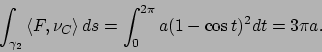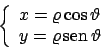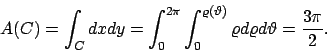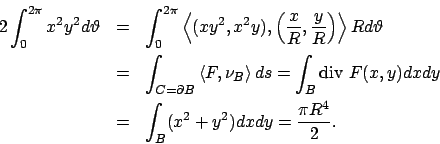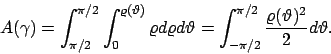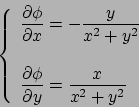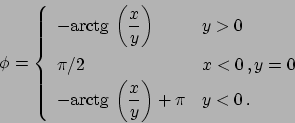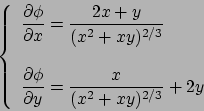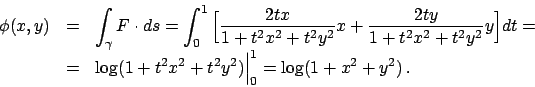Next: About this document ...
Up: 4esercizi
Previous: 4esercizi
ULTIMO AGGIORNAMENTO: 19. aprile 2004
![\begin{esercizio}\rm -\
Calcolare la lunghezza della curva
\begin{displaymath}
y=\log x, \quad x\in [3/4,4/3].
\end{displaymath}\end{esercizio}](img1.png)

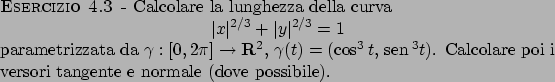


![\begin{esercizio}\rm -\
Calcolare l'integrale della funzione
\begin{displaymath...
...d{displaymath} lungo la curva $\gamma(t)=(t,t^2)$, $t\in [0,1]$.
\end{esercizio}](img6.png)
![\begin{esercizio}\rm -\
Calcolare l'integrale della funzione
\begin{displaymath...
...va $\varrho =e^{2\vartheta }$ con $\vartheta \in (-\infty, 0]$.
\end{esercizio}](img7.png)

![\begin{esercizio}\rm -\
Calcolare l'area del dominio racchiuso dalla cardioide d...
... polari
$\varrho=(1-\cos\vartheta )$, $\vartheta \in [0,2\pi]$.
\end{esercizio}](img9.png)

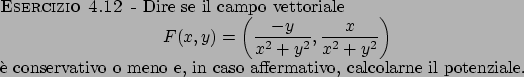
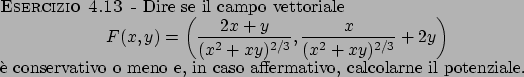




Soluzioni
Soluzione 4.1 -
La curva che stiamo considerando è data dalla funzione
![$\gamma:[3/4,4/3]\to{\bf R}^2$](img18.png) ,
,
quindi siccome
troviamo che
Soluzione 4.2 -
La curva che stiamo considerando può essere espressa
dalla funzione
![$\gamma :[0,2]\to {\bf R}^3$](img22.png) data da
data da
Quindi si ottiene che
 , da cui
, da cui
Soluzione 4.3 -
Il luogo dei punti che soddisfano
 è quello
disegnato in Figura 4.1.
Valutando la derivata di
è quello
disegnato in Figura 4.1.
Valutando la derivata di  si ottiene che in effetti
per i valori
si ottiene che in effetti
per i valori 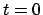 ,
, 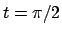 ,
, 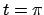 ,
, 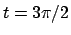 , corrispondenti
rispettivamente ai punti
, corrispondenti
rispettivamente ai punti 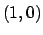 ,
, 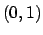 ,
, 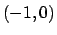 ,
,  , la curva non è
regolare. Si ha
, la curva non è
regolare. Si ha
`che ha modulo 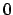 per i valori di
per i valori di 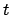 sopra elencati.
sopra elencati.
Figura 4.1:
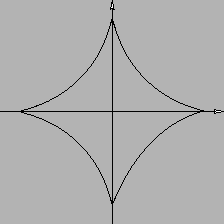 |
Il versore tangente si può trovare semplicemente dividendo 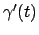 per il suo modulo
per il suo modulo 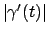 . Valutiamo quindi il modulo:
. Valutiamo quindi il modulo:
Si ha quindi che il vettore tangente 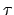 è dato da
è dato da
Nel primo quadrante, ad esempio, dove sia
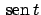 che
che 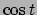 sono positivi,
si ha
sono positivi,
si ha
Derivando ulteriormente (ed eventualmente normalizzando nuovamente, ma in questo
caso non è necessario perché la derivata di 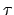 ha già norma
ha già norma 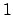 )
si ottiene il versore tangente
)
si ottiene il versore tangente 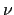
Valutare 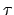 e
e 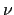 anche negli altri quadranti.
anche negli altri quadranti.
Soluzione 4.4 -
Per quanto riguarda la curva 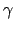 , se calcoliamo l'ascissa curvilinea
si ha che
, se calcoliamo l'ascissa curvilinea
si ha che
e quindi
Per la curva 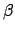 , si ha che l'ascissa curvilinea è data da
, si ha che l'ascissa curvilinea è data da
da cui
Per calcolare l'angolo 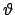 tra le due curve nel punto
tra le due curve nel punto 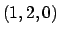 , bisogna
prima di tutto calcolare i valori di
, bisogna
prima di tutto calcolare i valori di 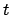 e
e 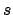 per i quali
per i quali
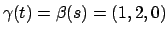 , e poi sfruttare la formula
, e poi sfruttare la formula
Si trova che 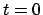 mentre
mentre 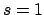 , da cui
, da cui
cioè 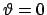 ; questo si può ricavare direttamente osservando
che
; questo si può ricavare direttamente osservando
che
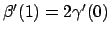 , cioè i due vettori
sono paralleli e con lo stesso verso.
, cioè i due vettori
sono paralleli e con lo stesso verso.
Soluzione 4.5 -
Calcoliamo l'ascissa curvilinea:
Quindi per poter riscrivere la curva in funzione di 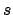 , bisogna ricavarsi
, bisogna ricavarsi 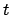 e sostituire, cioè
e sostituire, cioè
Provare a verificare che
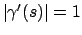 ; per calcolare la terna intrinseca, il
versore tangente è dato dalla velocità della curva normalizzata in modo da avere
norma
; per calcolare la terna intrinseca, il
versore tangente è dato dalla velocità della curva normalizzata in modo da avere
norma 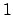 , cioè
, cioè
se si utilizza la parametrizzazione in 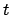 , mentre se si passa alla variabile
, mentre se si passa alla variabile
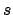 , si ha
, si ha
Si noti che il versore normale altro non è che
che come si può facilmente notare è parallelo alla velocità della curva ed ha
norma 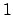 ; si noti infatti che
; si noti infatti che
Per quanto riguarda il versore normale, siccome
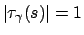 per ogni
per ogni 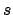 , allora se se ne
fa la derivata, non cambiando il modulo, si ottiene sempre e solo la variazione del verso di tale vettore,
e tale variazione è ortogonale a
, allora se se ne
fa la derivata, non cambiando il modulo, si ottiene sempre e solo la variazione del verso di tale vettore,
e tale variazione è ortogonale a 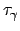 stesso. Quindi ha senso definire il versore normale
come tale derivata, normalizzata in modo da avere norma
stesso. Quindi ha senso definire il versore normale
come tale derivata, normalizzata in modo da avere norma 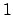 . Quindi in definitiva
. Quindi in definitiva
La binormale 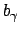 è semplicemente il versore normale ad entrambi i versori precedenti ed in modo tale
che
è semplicemente il versore normale ad entrambi i versori precedenti ed in modo tale
che
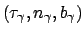 formino una terna sinistrorsa (come la terna cartesiana
formino una terna sinistrorsa (come la terna cartesiana
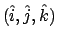 ).
Quindi si trova che
).
Quindi si trova che
Infine l'angolo con l'asse 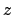 è dato dai prodotti scalari
è dato dai prodotti scalari
che non dipendono da 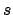 .
.
Soluzione 4.6 -
La curva è data da
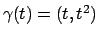 , quindi
, quindi
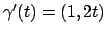 ,
da cui
,
da cui
Soluzione 4.7 -
La curva in questione è data da
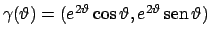 ,
e quindi l'integrale diventa
,
e quindi l'integrale diventa
Soluzione 4.8 -
L'arco di cicloide (si veda la Figura 4.2)
può essere pensato come la curva tracciata nel piano
da un punto fissato su un circonferenza che ruota sull'asse  (si pensi di fissare un punto sul copertone di una ruota di bicicletta
che corre, il cui raggio è
(si pensi di fissare un punto sul copertone di una ruota di bicicletta
che corre, il cui raggio è  ,
e di osservarne il movimento).
,
e di osservarne il movimento).
Figura 4.2:
 |
La derivata è data da
Si noti che il puntino sulla ruota è fermo per un istante ogni giro
(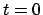 e
e 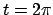 nel nostro caso, ma se la bicicletta prosegue per ogni
nel nostro caso, ma se la bicicletta prosegue per ogni 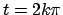 con
con 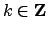 ),
mentre la componente
),
mentre la componente 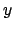 si annulla anche per
si annulla anche per 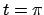 (quando la ruota ha percorso
mezzo giro). La lunghezza è data da
(quando la ruota ha percorso
mezzo giro). La lunghezza è data da
Per calcolare l'area si potrebbe passare alle coordinate polari (provare a farlo),
oppure utilizzare il teorema della divergenza. Procederemo seguendo questo secondo approccio;
l'area della cicloide 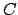 può essere calcolata tramite la formula
può essere calcolata tramite la formula
dove 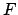 è un campo vettoriale con
è un campo vettoriale con
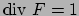 , il secondo integrale è l'integrale curvilineo
calcolato sulla curva
, il secondo integrale è l'integrale curvilineo
calcolato sulla curva
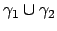 con
con
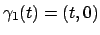 ,
, ![$t\in [0,2\pi]$](img101.png) e
e
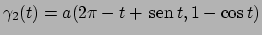 ,
, ![$t\in [0,2\pi]$](img101.png) . Campi
. Campi 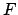 con la proprietà cercata sono
ad esempio
con la proprietà cercata sono
ad esempio
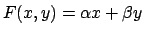 con
con
 ; nel nostro caso conviene
prendere
; nel nostro caso conviene
prendere 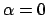 e
e 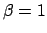 , in modo che
, in modo che 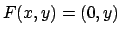 , e quindi l'itegrale
curvilineo di
, e quindi l'itegrale
curvilineo di 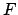 lungo
lungo 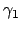 si annulla; resta solo il secondo integrale, che
diventa
si annulla; resta solo il secondo integrale, che
diventa
Soluzione 4.9 -
L'area della cardioide 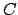 può essere calcolata usando le coordinate polari
può essere calcolata usando le coordinate polari
dove
![$\vartheta \in [0,2\pi]$](img111.png) , mentre a
, mentre a 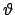 fissato il raggio
fissato il raggio 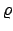 varia tra
varia tra
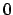 e
e
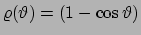 . Quindi
. Quindi
Allo stesso risultato si potrebbe giungere usando il teorema della divergenza; infatti
se 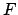 è un campo vettoriale con
è un campo vettoriale con
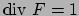 , allora
, allora
dove 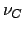 è la normale esterna alla cardioide e l'ultimo integrale è inteso
essere l'integrale curvilineo sul bordo di
è la normale esterna alla cardioide e l'ultimo integrale è inteso
essere l'integrale curvilineo sul bordo di 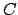 . Quindi se parametrizziamo
il bordo con la curva
. Quindi se parametrizziamo
il bordo con la curva
![$\vartheta \in [0,2\pi]$](img111.png) ; si ottiene quindi che
; si ottiene quindi che
mentre la normale esterna è data da
da cui, siccome
 ,
,
Soluzione 4.10 -
L'insieme  è una curva che può essere parametrizzata tramite
è una curva che può essere parametrizzata tramite
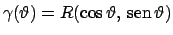 m
m
![$\vartheta \in [0,2\pi]$](img111.png) ;
per calcolare l'integrale, bisogna dare significato a
;
per calcolare l'integrale, bisogna dare significato a  e
e  .
Con un passaggio che andrebbe formalizzato meglio, si può dire
che se
.
Con un passaggio che andrebbe formalizzato meglio, si può dire
che se
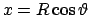 con
con 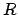 indipendente da
indipendente da 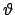 , allora
, allora
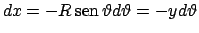 ; analogamente otteniamo che
; analogamente otteniamo che
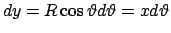 . Quindi si ha che
. Quindi si ha che
Si poteva ottenere lo stesso risultato utilizzando il teorema della divergenza;
infatti nel punto 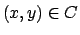 , la normale esterna è data da dal vettore
, la normale esterna è data da dal vettore
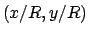 , mentre l'elemento di linea è dato da
, mentre l'elemento di linea è dato da
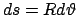 , da cui,
definendo il campo vettoriale
, da cui,
definendo il campo vettoriale
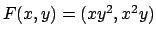 , si ha che
, si ha che
Soluzione 4.11 -
Data una curva chiusa
![$\gamma :[0,1]\to {\bf R}^2$](img135.png) , una prima osservazione
da fare è che se
, una prima osservazione
da fare è che se 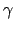 racchiude una regione di area massima, allora tale
regione deve essere convessa (se non lo fosse, se cioè ci
fosse una regione di non convessità, si potrebbe 'tappare' tale regione
convessificando l'insieme, operazione che aumenterebbe l'area della
regione senza aumentare il diametro dell'insieme). Quindi, se la regione
è convessa, ogni punto della curva vede ogni altro punto della curva stessa;
possiamo quindi porre un sistema di coordinate centrate in un punto
racchiude una regione di area massima, allora tale
regione deve essere convessa (se non lo fosse, se cioè ci
fosse una regione di non convessità, si potrebbe 'tappare' tale regione
convessificando l'insieme, operazione che aumenterebbe l'area della
regione senza aumentare il diametro dell'insieme). Quindi, se la regione
è convessa, ogni punto della curva vede ogni altro punto della curva stessa;
possiamo quindi porre un sistema di coordinate centrate in un punto 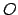 della
curva stessa in cui l'asse
della
curva stessa in cui l'asse 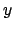 è tangente alla curva e l'asse
è tangente alla curva e l'asse 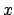 è perpendicolare
alla curva, diretto verso l'interno della curva. Scrivendo quindi la curva usando
coordinate polari centrate in tale punto
è perpendicolare
alla curva, diretto verso l'interno della curva. Scrivendo quindi la curva usando
coordinate polari centrate in tale punto 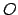 , otterremmo
, otterremmo
con
![$\vartheta \in [-\pi/2,\pi.2]$](img138.png) e a
e a 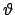 fissato, il raggio
fissato, il raggio 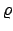 varia tra
varia tra 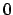 e un certo raggio
e un certo raggio
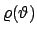 . Otteniamo quindi per
l'area che
. Otteniamo quindi per
l'area che
A questo punto notiamo che l'integrale possiamo restringerlo a
![$\vartheta \in [0,\pi/2]$](img141.png) ,
se oltre a
,
se oltre a
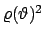 consideriamo anche
consideriamo anche
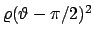 , e
notare infine che
, e
notare infine che
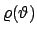 e
e
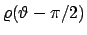 sono i due cateti
di un triangolo rettangolo la cui ipotenusa ha estremi che stanno sulla curva,
e quindi la sua lunghezza è minore del diametro dell'insieme, cioè
sono i due cateti
di un triangolo rettangolo la cui ipotenusa ha estremi che stanno sulla curva,
e quindi la sua lunghezza è minore del diametro dell'insieme, cioè
In definitiva, troviamo che
e quest'ultimo altro non è che l'area del cerchi di diametro  .
.
Soluzione 4.12 -
Se si considera il cammino chiuso
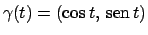 , si ottiene
che
, si ottiene
che
e quindi il campo risulta non essere conservativo. Otteniamo però che
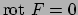 , quindi
, quindi 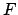 ammette potenziale locale
ammette potenziale locale 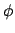 ; per calcolare tale potenziale
bisogna risolvere il sistema
; per calcolare tale potenziale
bisogna risolvere il sistema
che ha per soluzione, integrando la prima rispetto a 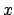 e sostituendo
nella seconda, la funzione
e sostituendo
nella seconda, la funzione
Il campo ammette quindi potenziale locale, ma il dominio è dato da
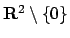 che non è semplicemente connesso; per rendere il campo
conservativo, dovremmo rendere il dominio semplicemente connesso, cosa che
può essere fatta se consideriamo il dominio
che non è semplicemente connesso; per rendere il campo
conservativo, dovremmo rendere il dominio semplicemente connesso, cosa che
può essere fatta se consideriamo il dominio
dove 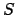 è una qualunque semiretta uscente dall'origine.
Consideriamo per semplicità il dominio
è una qualunque semiretta uscente dall'origine.
Consideriamo per semplicità il dominio 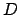 : un potenziale
: un potenziale 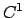 (verificare che è
(verificare che è 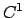 !) in
!) in 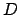 è dato allora dalla funzione
è dato allora dalla funzione
Soluzione 4.13 -
Notare che il dominio del campo è dato da
che è semplicemente connesso anche se non connesso. Quindi per vedere se il campo
è conservativo basta e serve che si abbia
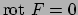 , cosa facilmente verificata. Per
trovare il potenziale locale
, cosa facilmente verificata. Per
trovare il potenziale locale 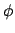 , bisogna risolvere il sistema
, bisogna risolvere il sistema
che ammette per soluzione la funzione
con la costante 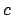 che può assumere valori diversi su ogni componente connessa.
che può assumere valori diversi su ogni componente connessa.
Soluzione 4.14 -
È facile vedere che il dominio naturale di 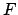 è
è 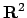 e che le derivate
incrociate sono uguali, per cui il campo è conservativo.
Per valutare un potenziale utilizziamo il fatto che per un campo conservativo
l'integrale
e che le derivate
incrociate sono uguali, per cui il campo è conservativo.
Per valutare un potenziale utilizziamo il fatto che per un campo conservativo
l'integrale
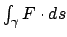 su
su 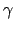 cammino che unisce
due punti
cammino che unisce
due punti 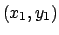 e
e 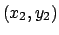 è indipendente dal cammino
è indipendente dal cammino 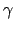 .
Possiamo fissare quindi arbitrariamente un punto, per comodità l'origine,
e il poyenziale in un generico punto
.
Possiamo fissare quindi arbitrariamente un punto, per comodità l'origine,
e il poyenziale in un generico punto 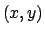 sarà dato
dall'integrale lungo quel cammino di
sarà dato
dall'integrale lungo quel cammino di 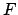 . Per semplicità scegliamo il cammino
che unisce l'origine a
. Per semplicità scegliamo il cammino
che unisce l'origine a 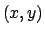 dato da
dato da
Si ha allora
Soluzione 4.15 -
Si noti che preso il cammino chiuso
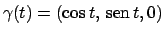 si ha
si ha
e quindi il campo non è conservativo. Però si ha che
 ,
e quindi il campo ammette potenzile locale, che si ricava essere
,
e quindi il campo ammette potenzile locale, che si ricava essere
Soluzione 4.16 -
Il dominio è semplicemente connesso e
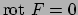 , quindi il campo
è conservativo. Il potenziale infine è dato dalla funzione
, quindi il campo
è conservativo. Il potenziale infine è dato dalla funzione
Soluzione 4.17 -
Il dominio è semplicemente connesso e
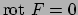 , quindi il campo è conservativo, e il
potenziale è dato da
, quindi il campo è conservativo, e il
potenziale è dato da
Si nota inoltre abbastanza immediatamente che per il campo elettrico 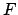 si
ha che
si
ha che
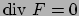 ; come per i campi vettoriali il cui rotore è nullo si
dimostra che ammette un potenziale, cioè una funzione il cui gradiente è
il campo, anche per i campi la cui divergenza è nulla si può dimostrare
che esiste un qualche potenziale, quello che si chiama il potenziale vettore,
cioè una funzione vettoriale
; come per i campi vettoriali il cui rotore è nullo si
dimostra che ammette un potenziale, cioè una funzione il cui gradiente è
il campo, anche per i campi la cui divergenza è nulla si può dimostrare
che esiste un qualche potenziale, quello che si chiama il potenziale vettore,
cioè una funzione vettoriale
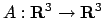 tale che
tale che



Next: About this document ...
Up: 4esercizi
Previous: 4esercizi
Fabio Paronetto
2004-04-19

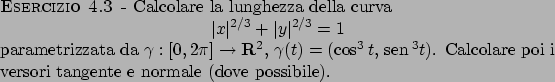


![\begin{esercizio}\rm -\
Calcolare l'integrale della funzione
\begin{displaymath...
...d{displaymath} lungo la curva $\gamma(t)=(t,t^2)$, $t\in [0,1]$.
\end{esercizio}](img6.png)
![\begin{esercizio}\rm -\
Calcolare l'integrale della funzione
\begin{displaymath...
...va $\varrho =e^{2\vartheta }$ con $\vartheta \in (-\infty, 0]$.
\end{esercizio}](img7.png)

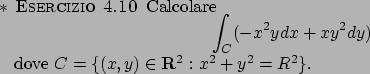

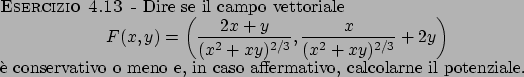




![]() ,
,