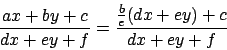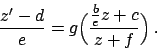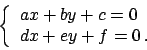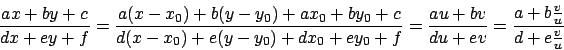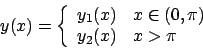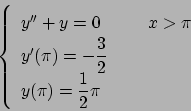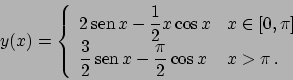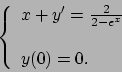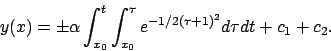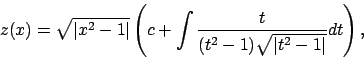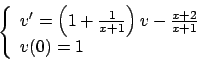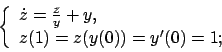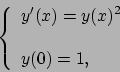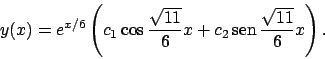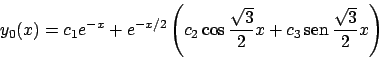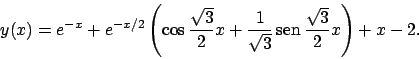Next: About this document ...
Up: 5esercizi
Previous: 5esercizi
ULTIMO AGGIORNAMENTO: 24. giugno 2005
Equazioni lineari di primo grado
Ricordo: per le equazioni di primo grado del tipo
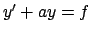 (dove
(dove 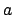 e
e 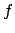 sono noti) una soluzione è data da
sono noti) una soluzione è data da
![\begin{displaymath}
y(t) = e^{-A(t)} \Big[ \int e^{A(t)} f(t) dt + c \Big]
\end{displaymath}](img4.png) |
(5.1) |
dove 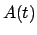 è una primitiva di
è una primitiva di 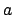 .
.



Equazioni a variabili separabili
Sono equazioni del tipo
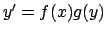 con
con 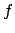 e
e 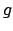 continue. La funzione
continue. La funzione 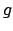 deve essere diversa da zero (si veda l'ESERCIZIO 5.5.
Si divide per
deve essere diversa da zero (si veda l'ESERCIZIO 5.5.
Si divide per 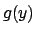 , si integra
, si integra
dopodiché si inverte la primitiva di 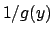 in modo da esplicitare
in modo da esplicitare  .
.
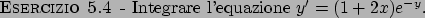


Equazioni di Bernoulli
Sono equazioni del tipo
con
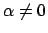 ,
,
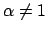 (per
(per 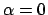 o
o 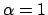 l'equazione è lineare).
Si divide per
l'equazione è lineare).
Si divide per 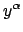 e si cambia variabile ponendo
e si cambia variabile ponendo
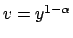 . Si ottiene
. Si ottiene
che nella nuova variabile diventa lineare


Equazioni di tipo omogeneo
Sono equazioni della forma
 con
con 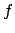 continua.
Si risolvono con il cambio di variabile
continua.
Si risolvono con il cambio di variabile
che porta all'equazione a variabili separabili
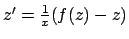 .
Dividendo per
.
Dividendo per 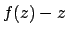 si ottiene l'equazione
si ottiene l'equazione
Deve essere quindi 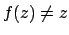 il che significa
il che significa
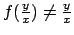 , ma nel caso
, ma nel caso
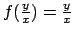 l'equazione si risolve direttamente.
Se si ha una condizione iniziale
l'equazione si risolve direttamente.
Se si ha una condizione iniziale 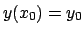 si deve avere
si deve avere 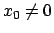 .
.
Alcune equazioni di secondo grado
In generale le equazioni di secondo gardo in forma normale sono della forma
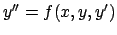 . Vedremo casi particolari:
. Vedremo casi particolari:
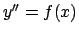 ,
,
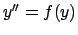 ,
,
 ,
,
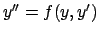 .
.
Si osservi che in realtà questi quattro esempi sono due, in quanto il caso
 è un caso particolare di
è un caso particolare di 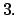 e il caso
e il caso 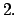 è un caso particolare di
è un caso particolare di 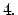 .
Vediamo come risolverle (si vedano anche i quattro esercizi che seguono).
.
Vediamo come risolverle (si vedano anche i quattro esercizi che seguono).
- Questo è l'esempio più semplice, è sufficiente integrare.
- Si può utilizzare il metodo spiegato al punto 4. oppure più semplicemente
moltiplicare l'equazione per
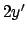 (
(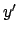 deve essere diversa da zero, quindi
se si risolve un problema di Cauchy si deve avere
deve essere diversa da zero, quindi
se si risolve un problema di Cauchy si deve avere
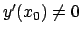 ). A questo punto
si ottiene
). A questo punto
si ottiene 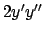 che può essere visto come
che può essere visto come
 .
Supponendo di dover risolvere (
.
Supponendo di dover risolvere (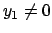 )
)
si ottiene
e integrando fra 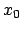 e
e 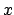 si ottiene
si ottiene
Se 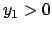 si considera
si considera
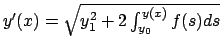 ,
se
,
se 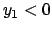 invece
invece
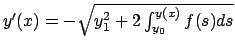 .
In entrambi i casi l'equazione è a variabili separabili.
.
In entrambi i casi l'equazione è a variabili separabili.
- È di fatto un'equazione del prim'ordine in
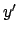 .
.
- Si effettua il cambio di variabile
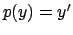 (attenzione!
(attenzione! 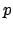 dipende da
dipende da  , cioè
, cioè
 viene vista come variabile indipendente, anche se poi sostituendo a
viene vista come variabile indipendente, anche se poi sostituendo a  la funzione
la funzione 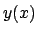 si ha
si ha
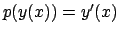 ). Si ottiene derivando rispetto a
). Si ottiene derivando rispetto a 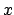
espressione che sostituita nell'equazione fornisce
dove però il segno  a sinistra denota la derivata di
a sinistra denota la derivata di 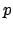 rispetto alla variabile
rispetto alla variabile
 (e non rispetto alla variabile
(e non rispetto alla variabile 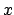 !).
Si integra, se si può, nella variabile
!).
Si integra, se si può, nella variabile  e una volta trovata
e una volta trovata 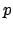 si integra
si integra
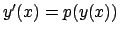 .
.
Le soluzioni di
equazioni del tipo 4. (e quindi anche del tipo 2.) non sempre sono esprimibili
in maniera esplicita (si veda la soluzione dell'ESERCIZIO 5.31).




Equazioni lineari a coefficienti costanti
Sono le equazioni del tipo
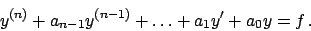 |
(5.2) |
Prima si risolve l'equazione omogenea
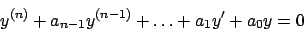 |
(5.3) |
trovando le soluzioni
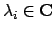 di (si vedano le dispense di teoria)
di (si vedano le dispense di teoria)
cosicché il polinomio potrà essere scritto anche
Denotando con  l'operatore differenziale
l'operatore differenziale
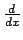 possiamo
riscrivere l'equazione (5.3) come segue
possiamo
riscrivere l'equazione (5.3) come segue
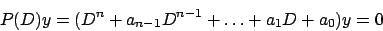 |
(5.4) |
cioè l'espressione
 può essere vista come un polinomio nella ``variabile''
può essere vista come un polinomio nella ``variabile''  applicato ad una funzione
applicato ad una funzione  cosicché, una volta trovate le radici
cosicché, una volta trovate le radici 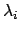 di
di 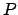 ,
si potrà scrivere
,
si potrà scrivere
Per trovare l'espressione generale della soluzione all'equazione non omogenea
può essere applicato il metodo della varizione delle costanti o dei parametri
(si veda, ad esempio, l'ESERCIZIO 5.19).
Tuttavia in qualche caso si può risparmiare lavoro
(esempi nell'ESERCIZIO 5.20, ESERCIZIO 5.21,
ESERCIZIO 5.22)
se ci si rende conto che
il dato 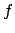 è soluzione di un'equazione a coefficienti costanti, cioè
esistono
è soluzione di un'equazione a coefficienti costanti, cioè
esistono
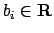 ,
,
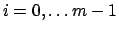 , tali che
, tali che
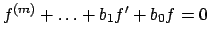 , cioè, denotando con
, cioè, denotando con 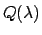 il polinomio
il polinomio
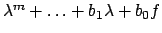 , possiamo scrivere
, possiamo scrivere
Supponendo allora che  sia una soluzione di (5.2) si avrà
sia una soluzione di (5.2) si avrà
che è come dire che  è soluzione di un'equazione omogenea di grado
è soluzione di un'equazione omogenea di grado 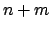 .
Denotate con
.
Denotate con
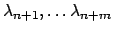 le radici del polinomio
le radici del polinomio 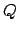 si può scrivere
si può scrivere
Trovate tutte le radici si può cercare  tra le soluzioni della precedente
equazione omogenea (attenzione! e non tra le soluzioni dell'equazione
tra le soluzioni della precedente
equazione omogenea (attenzione! e non tra le soluzioni dell'equazione 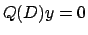 ,
si veda l'ESERCIZIO 5.22 per un esempio).
,
si veda l'ESERCIZIO 5.22 per un esempio).
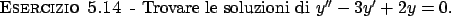
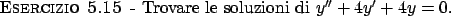
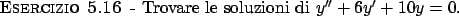
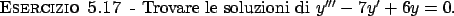


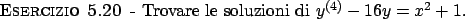
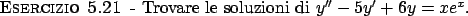

Esercizi di vario genere
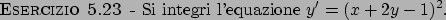
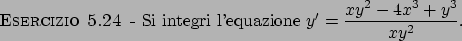

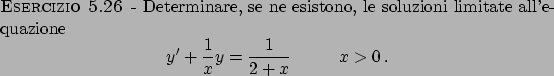
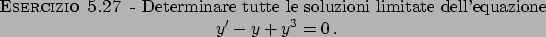

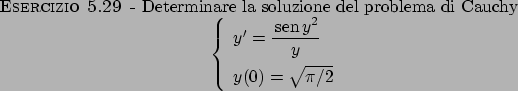

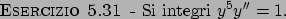






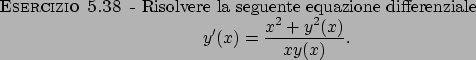
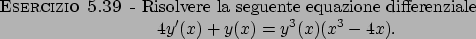
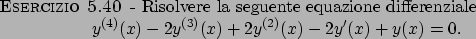
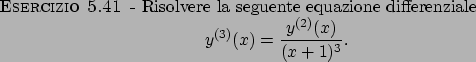
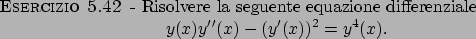
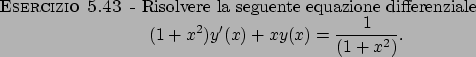
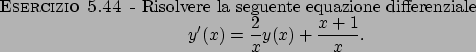
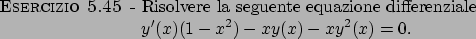
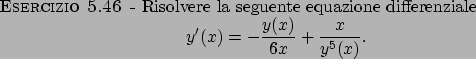

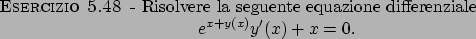
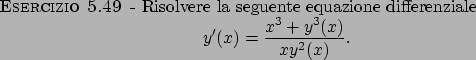



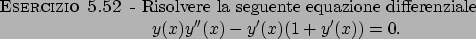

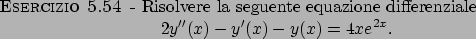
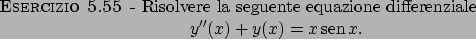
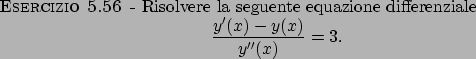
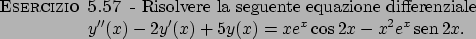

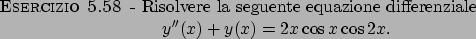

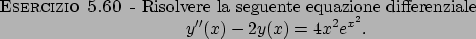
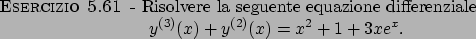
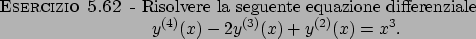
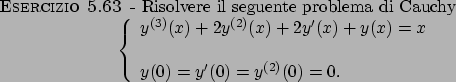
Soluzioni
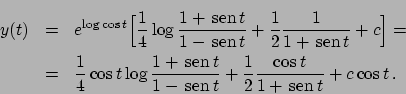
Soluzione 5.1 -
Usando l'espressione (5.1) calcoliamo prima una primitiva di
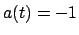 ,
, 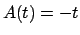 , poi
, poi
Si osservi che i grafici non si intersecano (disegnare i grafici di 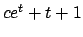 al variare di
al variare di 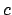 );
infatti considerando
);
infatti considerando
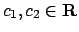 si ha che
si ha che
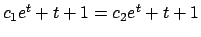 per qualche
per qualche 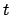 solo se
solo se 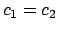 .
Ciò è dovuto al fatto che l'equazione, fissato un dato valore di
.
Ciò è dovuto al fatto che l'equazione, fissato un dato valore di  in un punto
in un punto 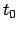 ,
ha soluzione unica.
,
ha soluzione unica.
Soluzione 5.2 -
Usando l'espressione (5.1) calcoliamo prima una primitiva di
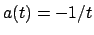 , che è continua in
, che è continua in
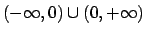 ,
,
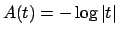 , infine
, infine
definite in  e in
e in 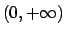 (si veda la Figura 5.1).
Poiché
(si veda la Figura 5.1).
Poiché 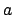 non è continua in
non è continua in 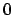 l'equazione non si può risolvere con un dato iniziale
l'equazione non si può risolvere con un dato iniziale
Figura 5.1:
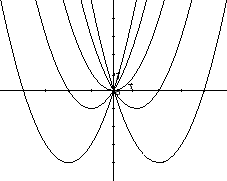 |
Si osservi però che, poiché il limite per 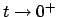 e
e 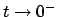 delle soluzioni è zero,
nel caso in cui
delle soluzioni è zero,
nel caso in cui 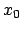 sia
sia 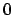 , si possono cercare soluzioni
, si possono cercare soluzioni 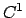 su tutto
su tutto 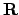 scegliendo
scegliendo
Si osservi che tutte queste sono soluzioni del problema con dato iniziale nullo in 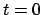 , quindi poiché
, quindi poiché
 non è continua in zero il problema di Cauchy non ha soluzione con dato iniziale definito per
non è continua in zero il problema di Cauchy non ha soluzione con dato iniziale definito per 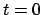 oppure se ha soluzione questa può non essere unica (in questo caso infinite).
oppure se ha soluzione questa può non essere unica (in questo caso infinite).
Soluzione 5.3 -
Questo problema ha una sola soluzione. Valutiamo prima una primitiva di
 :
:
Si osservi che
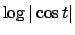 è definita per
è definita per
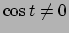 ed è quindi
continua negli intervalli
ed è quindi
continua negli intervalli
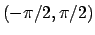 ,
,
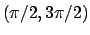 e così via
(in tutti gli intervalli del tipo
e così via
(in tutti gli intervalli del tipo
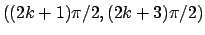 con
con 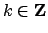 ).
Poiché siamo interessati a trovare una soluzione in un intorno di
).
Poiché siamo interessati a trovare una soluzione in un intorno di 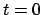 consideriamo come primitiva di
consideriamo come primitiva di
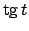 la funzione
la funzione 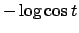 perché
intorno a
perché
intorno a 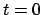 il coseno è positivo.
il coseno è positivo.
Ora valutiamo
Ponendo
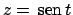 l'integrale diviene
l'integrale diviene
Scrivendo
si ottiene
per cui integrando si ottiene
per cui
e quindi infine
Per trovare la soluzione valuto 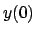 e impongo che valga
e impongo che valga 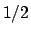 :
:
da cui 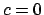 . La soluzione è
. La soluzione è
Si calcoli il limite per
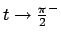 e
e
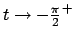 di
di  e della sua derivata
(si ottiene
e della sua derivata
(si ottiene
Soluzione 5.4 -
Dividendo per 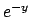 si ottiene
si ottiene
Integrando
da cui
per cui le soluzioni sono
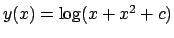 .
.
Soluzione 5.5 -
Denotiamo con 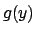 la funzione
la funzione 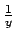 che è continua in
che è continua in
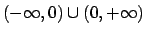 .
Questo significa che il problema può essere risolto se
.
Questo significa che il problema può essere risolto se 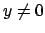 , cioè per un dato iniziale
, cioè per un dato iniziale
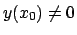 .
.
Si ha semplicemente 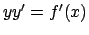 da cui
da cui
Se 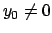 ricavando
ricavando 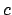 da
da
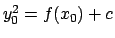 si ottiene che la soluzione è
si ottiene che la soluzione è
Si osservi che
la funzione 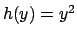 non è invertibile nel punto
non è invertibile nel punto 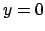 (e
(e 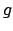 non è definita in
non è definita in 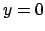 ). Questo fa sì
che non si possa ricavare
). Questo fa sì
che non si possa ricavare 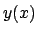 se il dato iniziale è
se il dato iniziale è 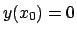 .
.
A titolo di esempio, vediamo un problema con il dato iniziale
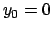 il quale potrebbe comunque avere soluzione
anche se
il quale potrebbe comunque avere soluzione
anche se 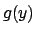 non è continua in
non è continua in 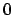 , ma in questo caso si perde l'unicità.
Si consideri
, ma in questo caso si perde l'unicità.
Si consideri
L'equazione ha come soluzioni 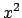 e
e 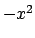 definite in
definite in 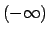 e in
e in 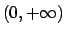 .
Poiché queste soluzioni in
.
Poiché queste soluzioni in 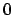 valgono
valgono 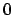 e il limite in
e il limite in 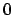 delle loro derivate è zero
si possono prolungare le soluzioni anche in zero scegliendo una soluzione nell'intervallo
delle loro derivate è zero
si possono prolungare le soluzioni anche in zero scegliendo una soluzione nell'intervallo
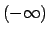 raccordandola con un'altra soluzione definita nell'intervallo
raccordandola con un'altra soluzione definita nell'intervallo 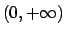 .
Si avrebbe che le seguenti quattro funzioni soddisfano il precedente problema di Cauchy
.
Si avrebbe che le seguenti quattro funzioni soddisfano il precedente problema di Cauchy
Soluzione 5.6 -
Dividendo per 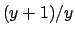 (cosa che si può fare solo
se
(cosa che si può fare solo
se 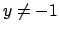 visto che questa funzione si annulla per
visto che questa funzione si annulla per 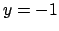 )
e integrando si ha
)
e integrando si ha
che fornisce l'espressione
Questo se 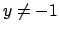 . Se
. Se 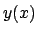 fosse
fosse 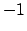 per un qualche valore di
per un qualche valore di 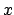 si ha che
l'equazione
si ha che
l'equazione
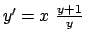 in quel punto diventa
in quel punto diventa
Quindi
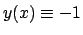 è soluzione dell'equazione (che non viene trovata con il metodo
precedente poiché si è diviso
è soluzione dell'equazione (che non viene trovata con il metodo
precedente poiché si è diviso
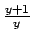 ).
).
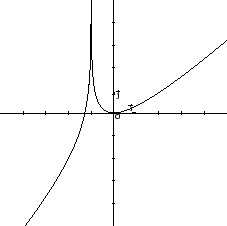
Si osservi inoltre che la funzione
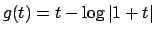 non è invertibile in un intorno di
non è invertibile in un intorno di
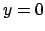 (si veda il grafico in Figura 5.2).
(si veda il grafico in Figura 5.2).
Figura 5.2:
 |
Quindi se si avesse un problema di Cauchy con 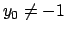 ,
, 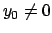
la soluzione sarebbe data, in forma implicita, da
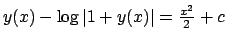 con la condizione
con la condizione
dalla quale si ricava il valore di 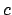 .
Formalmente (perché in questo caso non è semplice invertire
.
Formalmente (perché in questo caso non è semplice invertire
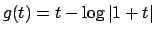 ) la soluzione sarebbe
) la soluzione sarebbe
dove 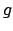 è invertibile, ma ci si accontenta della forma implicita.
Se
è invertibile, ma ci si accontenta della forma implicita.
Se 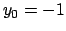 la soluzione è data da
la soluzione è data da
Soluzione 5.7 -
Dividendo per  si ottiene
si ottiene
e ponendo 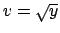 si ha l'equazione
si ha l'equazione
La soluzione è
da cui si ricava
Di conseguenza (
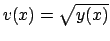 )
)
La condizione iniziale la si ricava imponendo
da cui
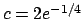 .
.
Soluzione 5.8 -
Anche questa è di Bernoulli con 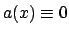 . Dividendo per
. Dividendo per  si ottiene
si ottiene
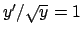 e ponendo
e ponendo
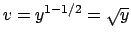 si ottiene
si ottiene
Risolvendo si ha
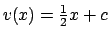 e imponendo la condizione iniziale
si ottiene
e imponendo la condizione iniziale
si ottiene
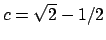 . Elevando al quadrato
. Elevando al quadrato
Soluzione 5.9 -
L'equazione è del tipo 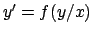 con
con
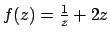 .
Effettuando il cambio di variabile si ottiene l'equazione
.
Effettuando il cambio di variabile si ottiene l'equazione
e separando le variabili
che integrata fornisce
da cui, ponendo
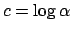 con
con  ,
,
La condizione iniziale per  si trasforma per la funzione
si trasforma per la funzione 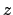 come segue
come segue
per cui fra le due possibili soluzioni si scelga quella che per 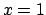 possa assumere
il valore
possa assumere
il valore 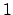 , cioè quella positiva
, cioè quella positiva
e non
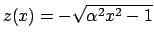 . A questo punto si ricavi il valore di
. A questo punto si ricavi il valore di
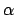 imponendo
imponendo
da cui
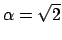 . La soluzione è allora
. La soluzione è allora
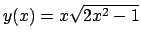 .
.
Soluzione 5.10 -
Integrando fra 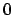 e
e 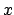 si ottiene
si ottiene
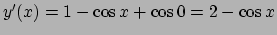 e integrando nuovamente fra
e integrando nuovamente fra 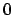 e
e 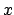 si ottiene
si ottiene
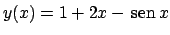 .
.
Soluzione 5.11 -
Moltiplichiamo per 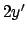 , integriamo e otteniamo
, integriamo e otteniamo
per cui separando le variabili
Integrando fra 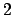 e
e 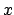
cioè
da cui si ricava
Soluzione 5.12 -
Sostituendo 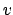 al posto di
al posto di 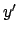 si ottiene l'equazione del primo ordine
si ottiene l'equazione del primo ordine
che si integra con usando la formula (5.1) che fornisce
A questo punto è sufficiente integrare l'equazione
che fornisce l'espressione generale della soluzione dell'equazione
Soluzione 5.13 -
Ponendo 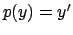 si perviene all'equazione
si perviene all'equazione
Integriamo: anziché considerare una generica primitiva si può integrare
fra estremi definiti. Partendo dai valori in 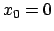 si ha
si ha
cioè
Ora sostituendo a 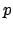
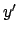 si ha
si ha
Integrando nuovamente (separando le variabili)
si ottiene
da cui infine si ricava
Soluzione 5.14 -
La soluzione è
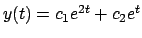 .
.
Soluzione 5.15 -
Il polinomio
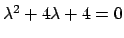 ha come soluzione
ha come soluzione 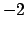 (con molteplicità due).
La soluzione è
(con molteplicità due).
La soluzione è
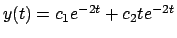 .
.
Soluzione 5.16 -
Il polinomio
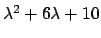 ha soluzioni complesse per cui la soluzione generale
ha la forma
ha soluzioni complesse per cui la soluzione generale
ha la forma
 .
.
Soluzione 5.17 -
La soluzione è
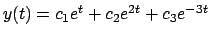 .
.
Soluzione 5.18 -
Si consideri il polinomio carattersistico
che si annulla per 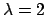 . Dividendo il polinomio per
. Dividendo il polinomio per 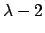 si ottiene che
si ottiene che
Quindi la soluzione generale è della forma
Valutando le derivate prima e seconda di  e valutandole per
e valutandole per 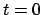 si ottiene
si ottiene
da cui si ricava che la soluzione è
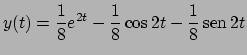 .
.
Soluzione 5.19 -
La soluzione generale dell'omogenea è
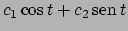 .
Utilizzando il metodo della variazione dei parametri,
cerco una soluzione all'equazione data del tipo
.
Utilizzando il metodo della variazione dei parametri,
cerco una soluzione all'equazione data del tipo
con 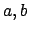 funzioni da determinarsi. Inserendo quest'espressione nell'equazione
arriviamo all'equazione
funzioni da determinarsi. Inserendo quest'espressione nell'equazione
arriviamo all'equazione
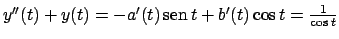 .
Risolvo quindi il sistema
.
Risolvo quindi il sistema
Ricavando 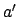 dalla prima equazione e sostituendo nella seconda si ottiene l'equazione
dalla prima equazione e sostituendo nella seconda si ottiene l'equazione
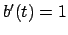 , da cui
, da cui
Quindi la soluzione generale dell'equazione è
con
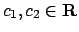 .
.
Soluzione 5.20 -
Il polinomio caratteristico
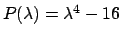 si annulla per
si annulla per
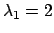 ,
,
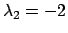 ,
,
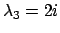 ,
,
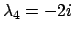 . La famiglia delle soluzioni dell'equazione
omogenea
. La famiglia delle soluzioni dell'equazione
omogenea
è allora
Anziché usare il metodo della variazione dei parametri (per esercizio risolvere
l'equazione anche con questo metodo) possiamo più semplicemente
osservare che
un polinomio che annulla il dato
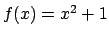 è
è 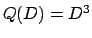 , infatti
, infatti
(in generale un polinomio di grado 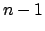 è annullato dal polinomio
è annullato dal polinomio 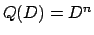 ).
La soluzione generale di
).
La soluzione generale di
è del tipo
Cerchiamo quindi una soluzione all'equazione non omogenea del tipo
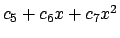 . Quindi imponendo
. Quindi imponendo
si ottengono
 e
e 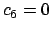 . Per concludere la soluzione generale
è
. Per concludere la soluzione generale
è
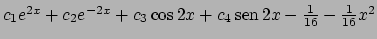 .
.
Soluzione 5.21 -
Il polinomio caratteristico è
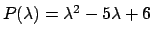 che ha come radici
che ha come radici 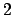 e
e 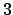 e l'equazione omogenea può essere scritta
e l'equazione omogenea può essere scritta
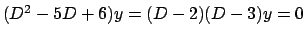 (da cui le soluzioni dell'omogenea sono
del tipo
(da cui le soluzioni dell'omogenea sono
del tipo
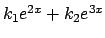 ).
Usando il metodo della variazione delle costanti o dei parametri cerchiamo
soluzioni del tipo
).
Usando il metodo della variazione delle costanti o dei parametri cerchiamo
soluzioni del tipo
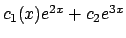 (
(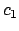 e
e 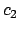 funzioni incognite).
Si perviene al sistema di equazioni
funzioni incognite).
Si perviene al sistema di equazioni
Dalla prima equazione si ottiene
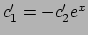 da cui, usando la seconda equazione,
si ottiene l'espressione
da cui, usando la seconda equazione,
si ottiene l'espressione
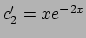 . Quest'equazione risolta fornisce
. Quest'equazione risolta fornisce
tramite la quale si trova anche
Inserendo 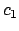 e
e 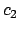 nell'espressione generale
si ottiene
nell'espressione generale
si ottiene
Possiamo evitare di usare questo metodo se osserviamo che
(si osservi che in generale
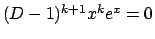 ).
Per cui la soluzione può essere cercata fra le soluzioni dell'equazione, detto
).
Per cui la soluzione può essere cercata fra le soluzioni dell'equazione, detto 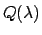 il
polinomio
il
polinomio
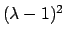 ,
,
Il polinomio
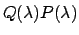 ha come radici
ha come radici 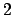 ,
, 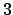 , e
, e 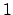 , quest'ultima con molteplicità
due. Per cui la soluzione
, quest'ultima con molteplicità
due. Per cui la soluzione 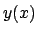 avrà la forma
avrà la forma
Applicando 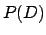 a questa funzione si ottiene
a questa funzione si ottiene
da cui si ricava che 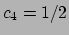 e
e 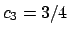 . Per cui la famiglia di soluzioni
è data, al variare di
. Per cui la famiglia di soluzioni
è data, al variare di
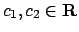 , da
, da
Soluzione 5.22 -
Le soluzioni dell'omogenea 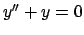 si ottengono trovando le soluzioni del polinomio
caratteristico
si ottengono trovando le soluzioni del polinomio
caratteristico
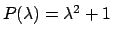 che sono
che sono 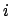 e
e 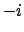 . Per cui le soluzioni di
. Per cui le soluzioni di
sono
 .
Per risolvere l'equazione completa
cerco un polinomio (un operatore differenziale) che annulla il dato
.
Per risolvere l'equazione completa
cerco un polinomio (un operatore differenziale) che annulla il dato
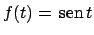 .
È ancora
.
È ancora 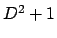 , cioè
, cioè
Cerco  tra le soluzioni dell'equazione omogenea
tra le soluzioni dell'equazione omogenea
(e non tra le soluzioni di
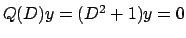 che sono le combinazioni lineari di
che sono le combinazioni lineari di
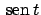 e
e  ). Le radici di
). Le radici di 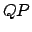 sono
sono 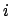 e
e 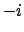 con molteplicità due, per cui
la soluzione va cercata tra le funzioni della forma
con molteplicità due, per cui
la soluzione va cercata tra le funzioni della forma
Applicando  alla famiglia di funzioni precedente si ha
alla famiglia di funzioni precedente si ha
che deve essere uguale a
 . Per cui la generica soluzione è
. Per cui la generica soluzione è
Soluzione 5.23 -
L'equazione è del tipo 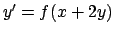 dove
dove
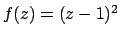 . Conviene
porre quindi
. Conviene
porre quindi
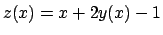 e scrivere
e scrivere
da cui
Si osservi che svolgendo il quadrato si ottiene
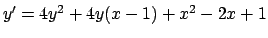 che non è di nessuno dei tipi visti
precedentemente. Risolvendo 'eqauzione nella nuova variabile si ottiene,
ponendo
che non è di nessuno dei tipi visti
precedentemente. Risolvendo 'eqauzione nella nuova variabile si ottiene,
ponendo
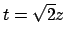 ,
,
da cui
e quindi infine
Soluzione 5.24 -
Innanzitutto si deve avere  .
L'equazione è omogenea: infatti
.
L'equazione è omogenea: infatti
con
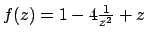 . Effettuando il cambio di variabile
. Effettuando il cambio di variabile
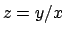 si perviene a
si perviene a
Separando le variabile si vede che deve essere 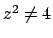 . Suppondendo allora
. Suppondendo allora
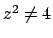 proseguiamo: scrivendo
proseguiamo: scrivendo
integrando l'equazione si ottiene
Per esercizio vedere che la funzione
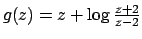 è invertibile in
è invertibile in 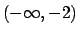 ,
in
,
in 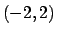 , in
, in  . Per cui sicuramente è possibile scrivere
. Per cui sicuramente è possibile scrivere
anche se la funzione 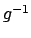 non riusciamo a scriverla, possiamo mantenerci una
scrittura implicita del tipo
non riusciamo a scriverla, possiamo mantenerci una
scrittura implicita del tipo
 |
(5.5) |
Rimane ancora il caso 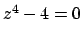 : in tal caso è semplice ottenere
: in tal caso è semplice ottenere
quindi le possibili soluzioni sono anche
 |
(5.6) |
Per cui se si avesse un problema di Cauchy
si sceglierebbe la soluzione data in (5.5) (la costante 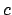 va trovata)
nell'intervallo
va trovata)
nell'intervallo  visto che se
visto che se 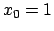 ,
, 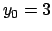 si ha che
si ha che
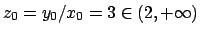 . Se invece si avesse lo stesso problema con un dato
differente
. Se invece si avesse lo stesso problema con un dato
differente
cioè 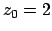 , la soluzione sarebbe
, la soluzione sarebbe 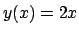 .
.
Soluzione 5.25 -
Dividendo per 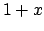 (che è positivo visto che siamo interessati ad una soluzione
in
(che è positivo visto che siamo interessati ad una soluzione
in 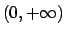 ) si ottiene l'equazione di Bernoulli
) si ottiene l'equazione di Bernoulli
che risolta fornisce
Effettuando il limite richiesto si ha che
per cui l'unica soluzione che soddisfa la richiesta è quella per cui 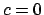 .
.
Soluzione 5.30 -
La soluzione localmente esiste (motivare perché).
Il dato 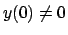 quindi localmente la soluzione sarà diversa da zero, per cui
possiamo dividere per
quindi localmente la soluzione sarà diversa da zero, per cui
possiamo dividere per  . Si ottiene
. Si ottiene
Effettuando il cambio di variabile spiegato al punto 4. del paragrafo dedicato alle
equazioni di secondo grado
si ottiene l'equazione nella incognita 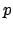 (e nella variabile
(e nella variabile  )
)
Integrando si ha
cioè
da cui
Attenzione! ci sono quattro possibilità visto che
Intergrando
si ottiene che
In ogni caso
Soluzione 5.31 -
Moltiplicando per 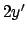 e dividendo per
e dividendo per 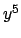 si ottiene
si ottiene
da cui
per cui
che rimane in forma implicita.
Soluzione 5.32 -
Se 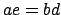 (il determinante della matrice
(il determinante della matrice
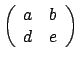 )
significa che le due rette
)
significa che le due rette 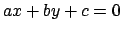 e
e 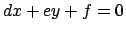 sono parallele.
Si può scrivere
sono parallele.
Si può scrivere
e ponendo 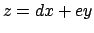 si perviene ad un'equazione a variabili separabili
si perviene ad un'equazione a variabili separabili
Se invece  si ottiene un'equazione omogenea nel modo seguente:
si cerca il punto d'incontro
si ottiene un'equazione omogenea nel modo seguente:
si cerca il punto d'incontro 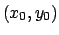 fra le due rette
fra le due rette 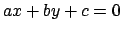 e
e 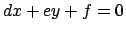 (che in questo caso non sono parallele) risolvendo il sistema
(che in questo caso non sono parallele) risolvendo il sistema
Introcendo le nuove variabili 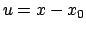 e
e 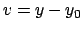 si può riscrivere
si può riscrivere
Ponendo
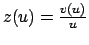 (
(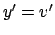 ) si perviene ad un'equazione
) si perviene ad un'equazione
Soluzione 5.33 -
Si veda lo svolgimento dell'ESERCIZIO 5.32
(si perviene alla forma implicita
e quindi la soluzione è data nella forma implicita
Soluzione 5.34 -
Si veda lo svolgimento dell'ESERCIZIO 5.32
(si perviene alla forma implicita
Soluzione 5.35 -
Innanzitutto si osservi che le soluzioni saranno infinite dal momento che manca
il dato relativo a 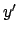 nel punto
nel punto 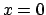 .
.
La funzione 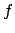 è continua in
è continua in 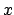 , non dipende da
, non dipende da  e
e 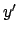 per cui il problema
ammette soluzione. Denotiamo
per cui il problema
ammette soluzione. Denotiamo
La soluzione per
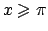 (
(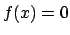 ) è del tipo
) è del tipo
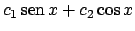 , per
, per
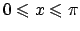 (
(
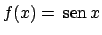 )
è del tipo
)
è del tipo
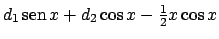 (si veda lo svolgimento dell'ESERCIZIO 5.22).
Per trovare
(si veda lo svolgimento dell'ESERCIZIO 5.22).
Per trovare 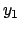 inseriamo i dati iniziali nel punto
inseriamo i dati iniziali nel punto 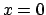 : si ottengono
: si ottengono
Di conseguenza la soluzione sarà
Per trovare  per
per 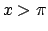 consideriamo l'espressione generale della soluzione
e poiché la soluzione in
consideriamo l'espressione generale della soluzione
e poiché la soluzione in 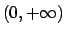 deve essere
deve essere 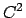 (visto che
(visto che 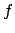 è continua) come dati iniziali
imponiamo i valori di
è continua) come dati iniziali
imponiamo i valori di 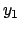 in
in 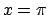 .
Si ha che
.
Si ha che
Risolviamo
il che significa trovare 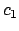 e
e 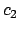 . Imponendo i dati iniziali nell'espressione
di
. Imponendo i dati iniziali nell'espressione
di 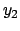 si ha
si ha
Concludendo la soluzione è
La soluzione è 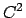 in quanto
in quanto 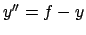 e sia
e sia 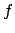 che
che  sono continue,
da cui anche
sono continue,
da cui anche 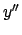 è continua
(verificarlo per esercizio).
è continua
(verificarlo per esercizio).
Soluzione 5.36 -
l'equazione proposta si presenta nella forma a variabili
separabili, cioè
Integrando quindi ambo i membri tra 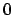 e
e 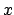 , si ottiene
, si ottiene
da cui
Soluzione 5.37 -
Ponendo
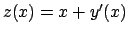 , l'equazione differenziale
può essere riscritta nella forma
, l'equazione differenziale
può essere riscritta nella forma
cioè
Questa è una equazione differenziale del prim'ordine
a variabili separabili, la cui soluzione è data da
se imponiamo le condizioni iniziali, notiamo che possiamo togliere il modulo
(perchè?) e troviamo che 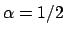 e quindi
e quindi
A questo punto il problema diventa
Tale problema ha per soluzione la funzione
Soluzione 5.38 -
Riscrivendo l'equazione nella forma
ci riconduciamo ad una equazione di tipo omogeneo
In questo tipo di equazioni si pone 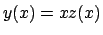 , in modo che
l'equazione diventi
, in modo che
l'equazione diventi
che si riconduce ad una equazione a variabili separabili.
Nel nostro caso troviamo che
da cui la soluzione del problema iniziale è data da
Soluzione 5.39 -
L'equazione proposta è una equazione di tipo Bernoulli; dividendo
infatti l'equazione per 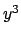 (si noti che tale operazione è lecita se si
cercano soluzioni non nulle), si ottiene
(si noti che tale operazione è lecita se si
cercano soluzioni non nulle), si ottiene
da cui, ponendo  , si ricava l'equazione
, si ricava l'equazione
Questa è una equazione differenziale lineare a coefficienti non costanti,
la cui soluzione è data da
La soluzione del problema sarà quindi data da
Soluzione 5.40 -
L'equazione data è una equazione lineare a coefficienti
costanti; le soluzioni le cerchiamo quindi nella forma
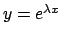 . Quindi tali funzioni sono soluzioni
se e solo se
. Quindi tali funzioni sono soluzioni
se e solo se 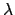 è una radice del polinomio caratteristico
è una radice del polinomio caratteristico
polinomio può essere riscritto nella forma
e quindi le radici complesse sono date da 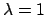 (con
molteplicità
(con
molteplicità 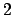 ) e
) e
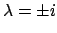 . La soluzione generale
sarà quindi data dalla funzione
. La soluzione generale
sarà quindi data dalla funzione
con
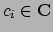 ,
, 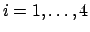 , oppure se si vogliono usare solo numeri reali
, oppure se si vogliono usare solo numeri reali
Soluzione 5.41 -
L'equazione di terzo grado assegnata può essere ridotta ad una
equazione del primo ordine con la sostituzione
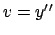 , da cui
, da cui
Tale equazione ha per soluzione
e quindi la soluzione del problema originale diventa
Soluzione 5.42 -
Si noti che nell'equazione data non compare la dipendenza da 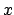 ; in
questo tipo di equazioni si cambia in qualche modo il punto di vista, e
si vede la funzione
; in
questo tipo di equazioni si cambia in qualche modo il punto di vista, e
si vede la funzione  come variabile libera e si cerca di esprimere
le varie derivate come derivate in funzione della variabile
come variabile libera e si cerca di esprimere
le varie derivate come derivate in funzione della variabile  . A tale
scopo si introduce la funzione
. A tale
scopo si introduce la funzione
e si calcola la derivata rispetto a  di tale funzione in modo
da ottenere
di tale funzione in modo
da ottenere
e quindi si ottiene l'equazione differenziale
che può essere riscritta come
otteniamo la soluzione
Si tratta quindi poi di risolvere l'equazione differenziale
Soluzione 5.43 -
L'equazione data è di tipo lineare a coefficienti non costanti, la cui
soluzione è data da
Soluzione 5.44 -
L'equazione data è una equazione lineare a coefficienti non costanti;
applicando quindi la formula risolutiva si trova che
Soluzione 5.45 -
l'equazione data è una equazione di tipo Bernoulli; con la sostituzione
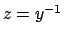 , si ottiene l'equazione lineare a coefficienti non costanti
, si ottiene l'equazione lineare a coefficienti non costanti
che ha per soluzione
che produce, a seconda dei dati iniziali, una delle seguenti due soluzioni
Quindi la soluzione originale sarà una delle due tra
e
Soluzione 5.46 -
L'equazione data è di tipo Bernoulli, e quindi con la sostituzione 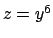 si ottiene la
soluzione
si ottiene la
soluzione
Se cerchiamo la soluzione per 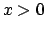 , integrando e tornando alla funzione
, integrando e tornando alla funzione  , si ottiene
, si ottiene
Soluzione 5.47 -
L'equazione data è a variabili separabili
e quindi la soluzione è data da
Soluzione 5.48 -
Riscrivendo l'equazione nella forma
notiamo che siamo ricondotti ad una equazione a variabili separabili,
la cui soluzione è data da
Soluzione 5.49 -
L'equazione data può essere ricondotta ad una equazione di tipo
omogeneo
che con la sostituzione 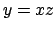 si riconduce all'equazione a variabili
separabili
si riconduce all'equazione a variabili
separabili
la cui soluzione è data da
Si tratta quindi poi di porre
Soluzione 5.50 -
L'equazione data può essere riscritta come
o meglio ancora come
Integrando quindi tra il punto iniziale 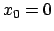 e
e 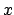 , si ottiene che
, si ottiene che
da cui si ricava, tenendo presente che
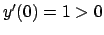 ,
,
La soluzione sarà quindi data da, tenendo presente che 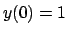 ,
,
Soluzione 5.51 -
Notando che nell'equazione non compare la  , si può porre
, si può porre
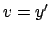 in modo da ottenere un'equazione lineare a coefficienti
non costanti
in modo da ottenere un'equazione lineare a coefficienti
non costanti
la cui soluzione è data da
La soluzione del problema iniziale sarà quindi data da
Soluzione 5.52 -
Nell'equazione data non compare la variabile 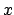 ,
quindi si può introdurre la funzione
,
quindi si può introdurre la funzione
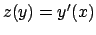 ;
con questa sostituzione otteniamo
;
con questa sostituzione otteniamo
si ottiene l'equazione
la soluzione di tale equazione è data da
Si tratta ora di risolvere il problema
la cui soluzione è data da
Soluzione 5.53 -
Come nell'esercizio precedente, nell'equazione non
compare la variabile 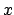 e quindi si pone
e quindi si pone 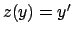 ;
si ottiene quindi che
;
si ottiene quindi che
e quindi il problema è risolto se si risolve l'equazione
dove la possibilità di togliere o meno il modulo dipenderà dai
dati iniziali; avremo quindi le due possibili soluzioni
Soluzione 5.54 -
L'equazione può essere riscritta nella forma
la soluzione dell'omogenea data da
mentre per la soluzione particolare si applica il
Teorema 5.23 delle dispense e si trova la funzione
La soluzione, imponendo le condizioni iniziali, sarà
quindi determinata da
Soluzione 5.55 -
La soluzione dell'omogenea è data da
per la determinazione della soluzione particolare
applichiamo il Teorema 5.23 delle dispense ed otteniamo
la funzione
La soluzione generale sarà quindi data da
Soluzione 5.56 -
La soluzione dell'omogenea è data da
per quanto riguarda la soluzione particolare si trova che
e quindi la soluzione generale è data da
Soluzione 5.57 -
L'equazione differenziale può essere riscritta nella
forma
e quindi si tratta di una equazione differenziale del secondo
ordine lineare omogenea a coefficienti costanti. Il suo polinomio
caratteristico è dato da
la soluzione generale sarà quindi data da
Soluzione 5.58 -
La soluzione dell'equazione omogenea è data da
Usando il Teorema 5.23 delle dispense, si trova
che la soluzione particolare è data da
La soluzione generale sarà data dalla somma delle due.
Soluzione 5.59 -
La soluzione dell'equazione omogenea è data
da
per quanto riguarda la soluzione particolare, si
applica il Teorema 5.23 delle dispense, si ottiene
A questo punto, imponendo le condizioni iniziali,
si ottiene la soluzione
Soluzione 5.60 -
La soluzione dell'omogenea è data da
per calcolare la soluzione particolare scriviamo
e quindi applicando il principio di sovrapposizione,
cioè tenendo conto che la soluzione particolare di
una somma di funzioni è data dalla somma delle soluzioni
particolari, dal Teorema 5.23 delle dispense, si ricava
che le soluzioni particolari sono date da
La soluzione generale sarà quindi data da
Soluzione 5.61 -
La soluzione dell'omogenea è data da
per calcolare la soluzione generale si applica il metodo della
variazione delle costanti, per ottenere la soluzione
Soluzione 5.62 -
La soluzione dell'equazione omogenea è data da
per quanto riguarda la soluzione particolare, usando il
metodo della variazioni delle costanti, si trova che
la soluzione generale è data da
Soluzione 5.63 -
La soluzione dell'equazione omogenea è data da
mentre per il calcolo della soluzione particolare
usiamo il principio di sovrapposizione delle soluzioni,
e cioè utilizziamo il fatto che quando il termine
forzante, la parte non omogenea dell'equazione differenziale,
è somma di più funzioni, allora la soluzione particolare
può essere determinata sommando le varie soluzioni particolari.
Utilizzando questo principio, abbiamo che associata a 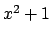 la soluzione particolare è data da
la soluzione particolare è data da
mentre associata a 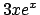 la soluzione particolare è data da
la soluzione particolare è data da
La soluzione generale sarà quindi data da
Soluzione 5.64 -
La soluzione dell'equazione omogenea è data da
mentre una soluzione particolare, grazie al Teorema
5.23 delle dispense, sarà data da
la soluzione generale sarà quindi data da
Soluzione 5.65 -
La soluzione dell'equazione omogenea è data da
mentre la soluzione particolare, ottenuta usando il metodo
illustrato nel Teorema 5.23 delle dispense, è data da
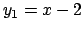 . Imponendo infine le condizioni iniziali, si
trova che la soluzione è data dalla funzione
. Imponendo infine le condizioni iniziali, si
trova che la soluzione è data dalla funzione



Next: About this document ...
Up: 5esercizi
Previous: 5esercizi
Fabio Paronetto
2005-06-24
![]() (dove
(dove ![]() e
e ![]() sono noti) una soluzione è data da
sono noti) una soluzione è data da





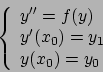
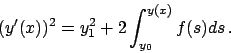
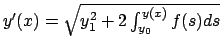 ,
se
,
se 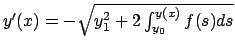 .
In entrambi i casi l'equazione è a variabili separabili.
.
In entrambi i casi l'equazione è a variabili separabili.





![]() ,
, ![]() , poi
, poi
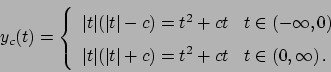
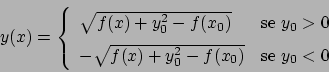

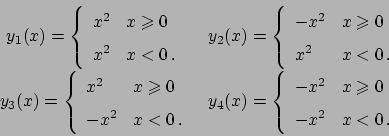
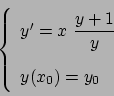
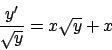

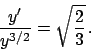
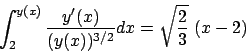
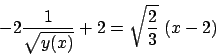
![\begin{displaymath}
\begin{array}{lll}
v(x) & = & e^{- \int [ - {{1}\over{x}} ] ...
... x + x \!\textrm{sen} \!x + c \vert x\vert .
\end{array}\end{displaymath}](img286.png)
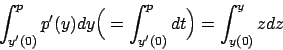
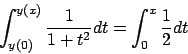
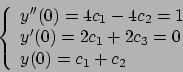
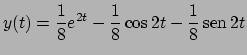 .
.
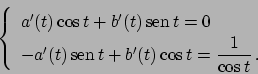
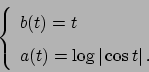
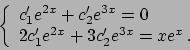
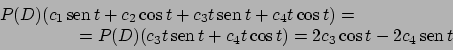
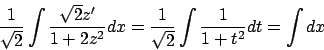
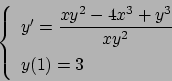
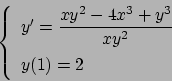
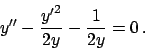
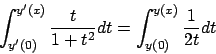
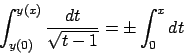
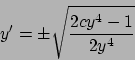
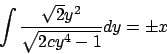
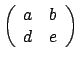 )
significa che le due rette
)
significa che le due rette