


Next: About this document ...
Up: 6esercizi
Previous: 6esercizi
ULTIMO AGGIORNAMENTO: 22. giugno 2005
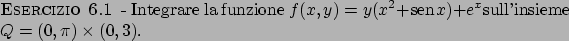
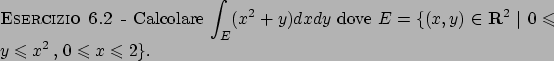
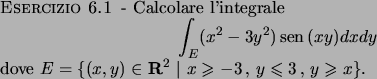
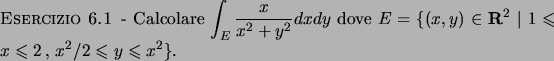
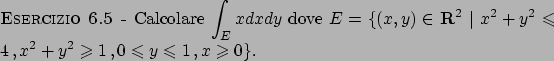
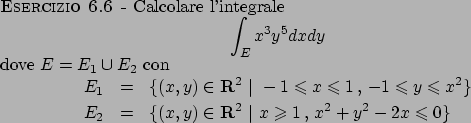
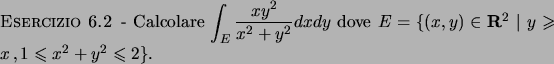
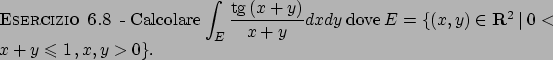
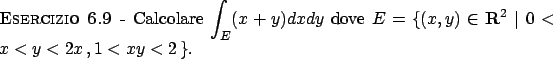
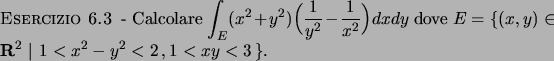
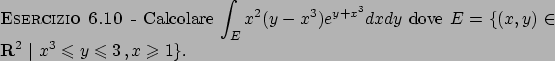
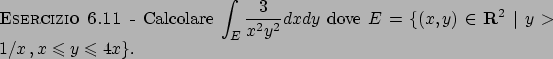
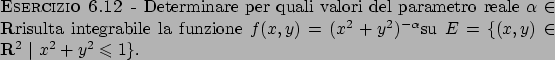
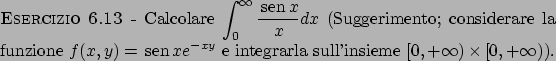
![\begin{esercizio}\rm -\
Calcolare l'area della regione $S$ compresa tra le curv...
...vartheta \in [-\pi/4,\pi/4].
\end{array}\right.
\end{displaymath}\end{esercizio}](img18.png)
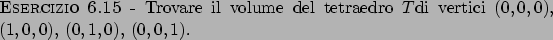
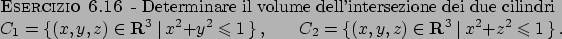
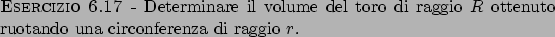
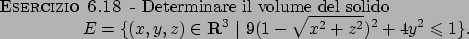
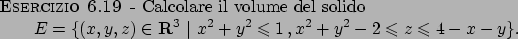
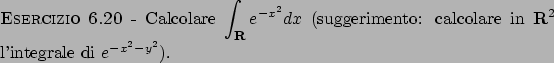

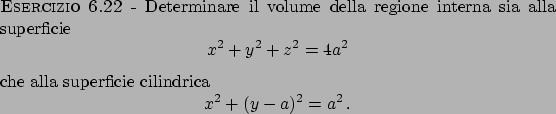
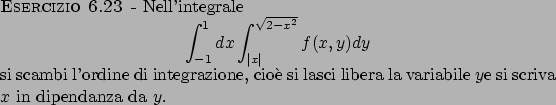
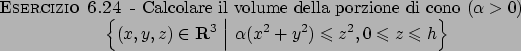
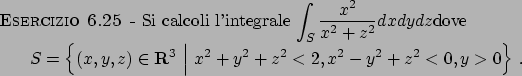
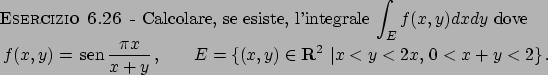
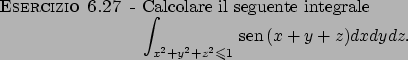
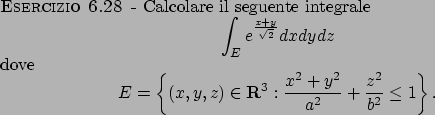
Integrali di superficie
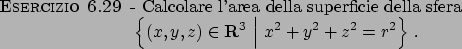

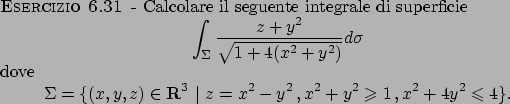
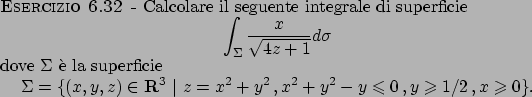
Flussi
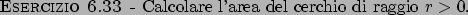
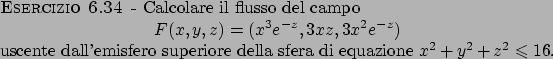
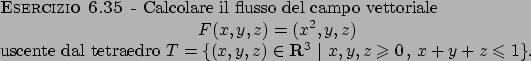

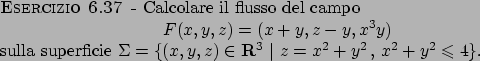
Soluzioni
Soluzione 6.1 -
Essendo il dominio un rettangolo si può scrivere
e integrare indifferentemente
prima rispetto ad una variabile e poi rispetto all'altra.
Scegliamo di integrare prima rispetto alla variabile 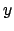 :
:
Soluzione 6.2 -
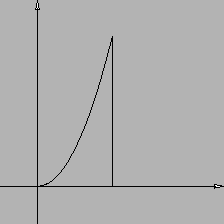
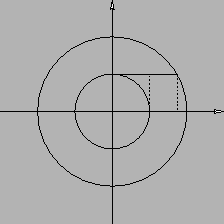
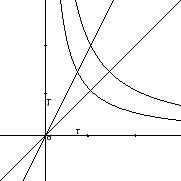
L'insieme  è quello rappresentato in Figura 6.1.
è quello rappresentato in Figura 6.1.
Figura 6.1:
 |
Scegliendo 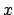 come variabile libera si può scrivere l'integrale
come variabile libera si può scrivere l'integrale
che diventa
Scegliendo 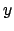 come variabile libera l'integrale diventa (svolgerlo per esercizio)
come variabile libera l'integrale diventa (svolgerlo per esercizio)
Soluzione 6.3 -
Il dominio di integrazione è normale rispetto
ad entrambe le variabili; scrivendo
conviene tenere nel primo integrale come variabile libera
la 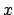 , mentre nel secondo conviene tenere come variabile libera la
, mentre nel secondo conviene tenere come variabile libera la
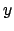 ; quindi
; quindi
in quanto integrali di funzioni dispari su intervalli simmetrici
rispetto all'origine.
Soluzione 6.4 -
Scegliendo 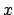 come variabile libera, l'integrale diventa
come variabile libera, l'integrale diventa
Soluzione 6.5 -
Se scegliamo 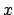 come variabile libera dobbiamo spezzare in tre l'integrale
(in tre insiemi come indicato in Figura 6.2).
come variabile libera dobbiamo spezzare in tre l'integrale
(in tre insiemi come indicato in Figura 6.2).
Figura 6.2:
 |
Conviene quindi scegliere 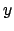 come variabile libera:
come variabile libera:
Soluzione 6.6 -
Notiamo anzitutto che la funzione integranda è dispari rispetto
ad entrambe le variabile, inoltre il dominio 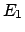 è simmetrico
rispetto all'asse
è simmetrico
rispetto all'asse 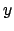 mentre
mentre 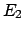 è simmetrico rispetto all'asse
è simmetrico rispetto all'asse
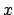 , quindi
, quindi
Soluzione 6.7 -
L'insieme di integrazione non è normale rispetto a nessuna
delle due variabili; notiamo però che se passiamo alle
coordinate polari, esso diventa, nelle variabili
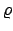 e
e 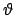 , il rettangolo
, il rettangolo
![$[1,\sqrt{2}]\times[\pi/4,5\pi/4]$](img60.png) .
Otteniamo quindi che
.
Otteniamo quindi che
Soluzione 6.8 -
Notiamo che il dominio di integrazione è normale rispetto ad
entrambe le variabili, però la funzione integranda
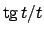 non
ammette primitiva; proviamo quindi ad effettuare.
Cerchiamo un cambio di variabili tale che la matrice
del cambiamento di coordinate abbia determinante
non
ammette primitiva; proviamo quindi ad effettuare.
Cerchiamo un cambio di variabili tale che la matrice
del cambiamento di coordinate abbia determinante 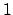 ; un possibile
cambio di variabili di questo tipo si può ottenere ponendo
; un possibile
cambio di variabili di questo tipo si può ottenere ponendo
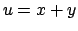 ,
, 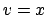 . Nelle variabili
. Nelle variabili 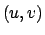 l'insieme
l'insieme 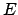 diventa
diventa
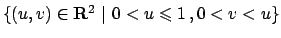 ,
e quindi
,
e quindi
Soluzione 6.9 -
L'insieme  è quello in Figura 6.3.
è quello in Figura 6.3.
Figura 6.3:
 |
Si può svolgere il calcolo in
coordianate cartesiane, ma è più semplice effettuare il cambio di coordinate
da cui si ricava che
Lo jacobiano di tale trasformazione è dato da 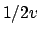 per cui si ottiene
per cui si ottiene
che svolto dà il risultato.
Soluzione 6.10 -
Ponendo 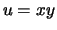 e
e 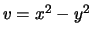 si ottiene che
si ottiene che
per cui lo jacobiano della matrice (inversa) del cambiamento di variabili è
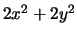 (cioè il cambio dalla coppia
(cioè il cambio dalla coppia 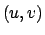 alla coppia
alla coppia 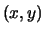 ).
Di conseguenza, poiché
).
Di conseguenza, poiché
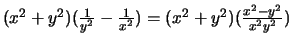 ,
l'integrale scritto nulle nuove variabili diventa
,
l'integrale scritto nulle nuove variabili diventa
Soluzione 6.11 -
Se effettuiamo la sostituzione 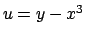 ,
, 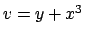 , notiamo che
la funzione
, notiamo che
la funzione
 è una applicazione
differenziabile con
è una applicazione
differenziabile con
e quindi eccettuato i punti in cui 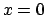 , la funzione
, la funzione
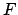 è un diffeomorfismo. Notiamo che sull'insieme
è un diffeomorfismo. Notiamo che sull'insieme 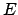 si ha
si ha 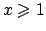 , e quindi possiamo applicare la formula
di cambiamento di variabili, tenendo presente che
nelle variabili
, e quindi possiamo applicare la formula
di cambiamento di variabili, tenendo presente che
nelle variabili 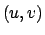 l'insieme
l'insieme 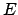 diventa
diventa
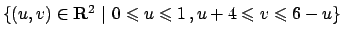 ,
,
Soluzione 6.12 -
Passando alle coordinate polari, l'insieme 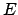 diventa
diventa
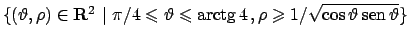 ; quindi l'integrale diventa
; quindi l'integrale diventa
Provare anche con il cambio di variabile 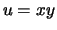 e
e 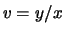 .
.
Soluzione 6.13 -
Passando alle coordinate polari otteniamo
e quindi la funzione sarà integrabile per 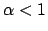 .
.
Soluzione 6.14 -
Se integriamo la funzione
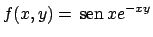 su
su
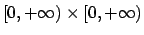 prima rispetto a
prima rispetto a 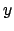 otteniamo
otteniamo
mentre se integriamo prima rispetto a 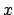 si ottiene
si ottiene
da cui si ricava che
Soluzione 6.15 -
Riscrivendo la prima curva, che è una circonferenza
centrata in 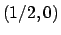 e raggio
e raggio 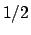 , in coordinate polari,
abbiamo che essa è descritta dall'equazione
, in coordinate polari,
abbiamo che essa è descritta dall'equazione
Figura 6.4:
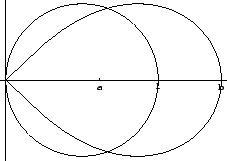 |
Notando a questo punto che il dominio 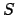 di cui si vuole
calcolare l'area è simmetrico rispetto all'asse
di cui si vuole
calcolare l'area è simmetrico rispetto all'asse 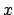 (si veda la figura (6.4)),
la sua area sarà data da
(si veda la figura (6.4)),
la sua area sarà data da
dove  è individuata, nelle coordinate polari,
da
è individuata, nelle coordinate polari,
da
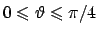 . Cerchiamo anzitutto l'angolo
. Cerchiamo anzitutto l'angolo 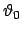 per il quale le due curve si incontrano; esso sarà individuato
dalla condizione
per il quale le due curve si incontrano; esso sarà individuato
dalla condizione
che ha come soluzione
L'area di  sarà quindi data da
sarà quindi data da
In definitiva
Soluzione 6.16 -
Il tetraedro è il solido delimitato dai quattro piani
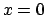 ,
, 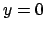 ,
, 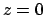 ,
, 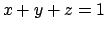 e rappresentato in Figura 6.5.
e rappresentato in Figura 6.5.
Figura 6.5:
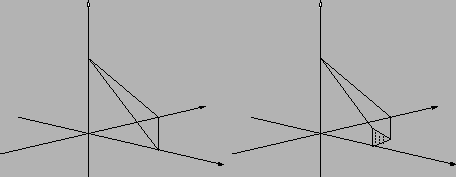 |
Per calcolare il volume di un solido 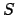 (e in generale la misura
(e in generale la misura 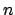 -dimensionale
di un aperto in
-dimensionale
di un aperto in 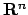 ) si può calcolare l'integrale della funzione
) si può calcolare l'integrale della funzione 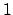 sull'insieme
sull'insieme 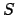 . Per cui valutiamo
. Per cui valutiamo
Scegliendo 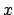 come variabile libera si hanno le limitazioni
come variabile libera si hanno le limitazioni
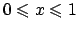 . Per
. Per 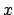 fissato ora esprimiamo gli estremi per
fissato ora esprimiamo gli estremi per 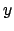 e
e 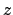 (si veda il secondo disegno in Figura 6.5).
Scegliendo
(si veda il secondo disegno in Figura 6.5).
Scegliendo 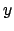 si ottiene
si ottiene
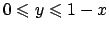 e infine
e infine
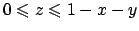 . Quindi
. Quindi
Soluzione 6.17 -
Chiamando 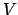 il solido dato dall'intersezione di
il solido dato dall'intersezione di 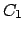 e
e 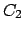 si ha
si ha
Soluzione 6.18 -
Il toro è una figura la cui superficie
può essere ottenuta ruotando una circonferenza di raggio 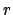 su una circonferenza di raggio
su una circonferenza di raggio 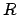 ortogonale alla prima,
ortogonale alla prima, 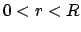 per ottenere una
figura come quella a sinistra in Figura 6.6.
per ottenere una
figura come quella a sinistra in Figura 6.6.
Figura 6.6:
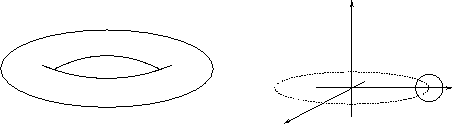 |
In generale per calcolare il volume di
un solido di rotazione, cioè un solido la cui superficie
si ottiene ruotando una curva 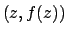 nel piano con
nel piano con 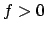 (si veda la Figura 6.7),
si possono usare le coordinate cilindriche.
(si veda la Figura 6.7),
si possono usare le coordinate cilindriche.
Figura 6.7:
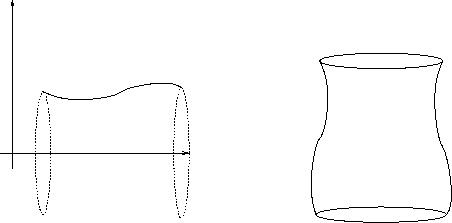 |
Considerando
![$f:[a,b] \to {\bf R}$](img136.png) ,
, 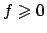 , e il solido ottenuto ruotando il grafico
di
, e il solido ottenuto ruotando il grafico
di 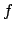 , descriviamo il solido con le coordinate
, descriviamo il solido con le coordinate
il cui jacobiano è  . Se denotiamo con
. Se denotiamo con 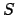 il solido, integrando si ha
il solido, integrando si ha
Per calcolare il volume del toro consideriamo quindi le funzioni
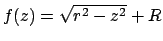 e
e
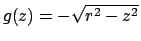 definite tra
definite tra 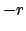 e
e 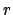 valutando prima l'integrale di
valutando prima l'integrale di 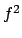 al quale sottraiamo l'integrale di
al quale sottraiamo l'integrale di  .
Si ha quindi
.
Si ha quindi
Si noti che l'integrale da calcolare fornisce l'area del semicerchio, per cui
il volume del toro è dato da
Si noti che questa quantità è data dal prodotto dell'area del cerchio piccolo
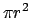 moltiplicata per la lunghezza della circonferenza grande
moltiplicata per la lunghezza della circonferenza grande 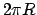 .
.
Soluzione 6.19 -
Notiamo che l'insieme dato è invariante per rotazioni attorno
all'asse 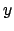 , quindi possiamo provare a passare alle coordinate
cilindriche con asse lungo l'asse
, quindi possiamo provare a passare alle coordinate
cilindriche con asse lungo l'asse 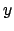 , cioè
, cioè
In queste nuove coordinate l'insieme 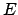 risulta essere determinato da
risulta essere determinato da
Otteniamo quindi che il volume di 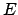 è dato da
è dato da
Soluzione 6.20 -
L'insieme di sui si vuole calcolare il volume è costituito
dalla la regione dello spazio in cui 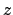 è compresa tra il paraboloide
è compresa tra il paraboloide
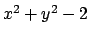 e il piano
e il piano 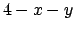 , mentre
, mentre 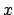 e
e 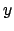 appartengono
alla palla
appartengono
alla palla 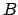 centrata nell'origine e di raggio
centrata nell'origine e di raggio 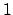 . Siccome
il paraboloide e il piano si incontrano quando
. Siccome
il paraboloide e il piano si incontrano quando
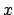 e
e 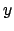 appartengono alla circonferenza
centrata in
appartengono alla circonferenza
centrata in 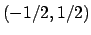 e raggio
e raggio 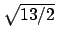 (circonferenza
che contiene la palla
(circonferenza
che contiene la palla 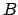 ),
abbiamo che il volume può essere calcolato come integrale
triplo della funzione
),
abbiamo che il volume può essere calcolato come integrale
triplo della funzione 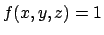 sul dominio
sul dominio 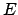 che è normale
rispetto alla variabile
che è normale
rispetto alla variabile 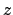 . Otteniamo quindi che
. Otteniamo quindi che
Quest'ultimo integrale può infine essere calcolato utilizzando
le coordinate polari, in modo da ottenere
Soluzione 6.21 -
La funzione
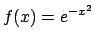 non ammette un'esplicita primitiva. Per calcolare
quest'integrale usiamo un trucco: passiamo attraverso un integrale in
non ammette un'esplicita primitiva. Per calcolare
quest'integrale usiamo un trucco: passiamo attraverso un integrale in 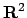 .
Valutiamo
.
Valutiamo
Usando le coordinate polari, il cui jacobiano è  , otteniamo
, otteniamo
D'altra parte
da cui si conclude che
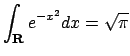 e più in generale
e più in generale
Soluzione 6.22 -
Uso le coordinate polari modificate che possiamo chiamare coordinate ellittiche
che ha jacobiano 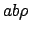 . L'area diventa
. L'area diventa
Soluzione 6.23 -
Sfruttando la simmetria sia rispetto al piano 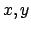 che rispetto al piano
che rispetto al piano
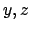 il volume del solido risulta essere quattro volte il volume
del solido delimitato inoltre dalle condizioni
il volume del solido risulta essere quattro volte il volume
del solido delimitato inoltre dalle condizioni 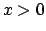 e
e 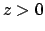 .
.
A questo punto usiamo le coordinate cilindriche con asse lungo l'asse 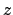 e centrate nell'origine:
il cilindro è determinato dall'equazione
e centrate nell'origine:
il cilindro è determinato dall'equazione
che equivalentemente può essere scritto come
che ha soluzioni 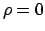 e
e
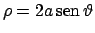 .
Quindi le limitazioni per le variabili sono
.
Quindi le limitazioni per le variabili sono
Infine da
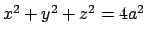 si ricava
si ricava
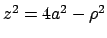 da cui le limitazioni sulla
da cui le limitazioni sulla 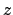 diventano
diventano
Quindi il volume è dato da
che fornisce, usando il fatto che per
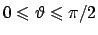
 , il seguente risultato
, il seguente risultato
Soluzione 6.24 -
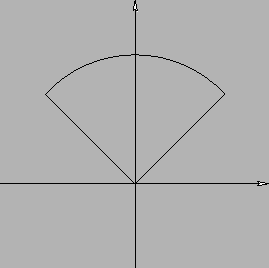
L'insieme delimitato dagli estremi 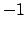 e
e 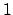 per la variabile
per la variabile 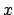 e
e 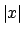 e
e 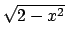 per la variabile
per la variabile 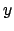 è quello in
Figura 6.8. Quindi l'integrale diventa
è quello in
Figura 6.8. Quindi l'integrale diventa
Figura 6.8:
 |
Soluzione 6.25 -
Uso le coordinate cilindriche
Provare alternativamente ad usare la formula per i solidi di rotazione
(si veda la soluzione dell'ESERCIZIO 6.18).
Soluzione 6.26 -
Utilizziamo le coordinate cilindriche
con
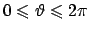 ,
,
 e
e
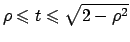 .
L'integrale diventa
.
L'integrale diventa
Provare anche ad utilizzare le coordinate sferiche (opportunamente!).
Soluzione 6.27 -
L'insieme 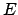 è quello a sinistra in Figura 6.9.
Sicuramente l'integrale esiste perché la funzione integranda è limitata
e quindi
è quello a sinistra in Figura 6.9.
Sicuramente l'integrale esiste perché la funzione integranda è limitata
e quindi
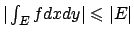 .
.
Un modo di risolvere questo integrale è effettuare il cambio di variabile
Figura 6.9:
a sinistra l'insieme 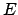 , a destra
, a destra 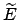
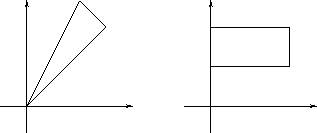 |
che porta il rettangolo
 in
in  .
Il cambio
.
Il cambio 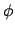 si ottiene ponendo
si ottiene ponendo 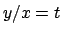 e
e 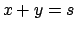 .
Lo jacobiano è dato da
.
Lo jacobiano è dato da
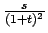 , per cui si perviene all'integrale
, per cui si perviene all'integrale
che risolto è
Provare anche con il cambio di variabile
che mappa
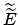 in
in 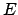 come indicato in Figura 6.10.
come indicato in Figura 6.10.
Figura 6.10:
a sinistra l'insieme 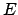 ,
a destra
,
a destra
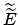
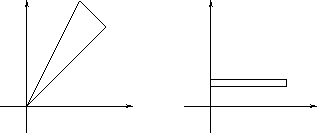 |
Soluzione 6.28 -
Per calcolare l'integrale dato, proviamo ad effettuare un cambio
di variabili in modo che la funzione integranda si semplifichi
ed in modo tale che la matrice del cambiamento di coordinate
non dia problemi nell'integrazione e, ancora, che nel nuovo
sistema di riferimento l'insieme su cui si vuole integrare
non si complichi. Un modo per non avere problemi con la matrice
del cambiamento di coordinate è fare in modo che tale matrice abbia
determinante pari a 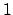 ; particolari trasformazioni
con tale determinante sono le rotazioni, trasformazioni
che hanno il vantaggio nel nostro caso di trasformare la
palla
; particolari trasformazioni
con tale determinante sono le rotazioni, trasformazioni
che hanno il vantaggio nel nostro caso di trasformare la
palla  centrata nell'origine e di raggio
centrata nell'origine e di raggio  in se stessa.
Cerchiamo quindi una rotazione dello spazio che ad esempio mandi
il piano
in se stessa.
Cerchiamo quindi una rotazione dello spazio che ad esempio mandi
il piano 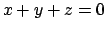 nel piano determinato nelle nuove
coordinate
nel piano determinato nelle nuove
coordinate 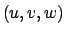 ad esempio da
ad esempio da 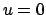 . Una tale
rotazione è data ad esempio
. Una tale
rotazione è data ad esempio

Con tale trasformazione si ottiene che l'integrale diventa
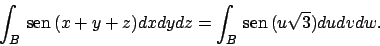
A questo punto notiamo che la funzione integranda è dispari
nella variabile 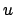 e il dominio
e il dominio 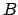 è simmetrico rispetto
a tale variabile, e quindi si ottiene che
è simmetrico rispetto
a tale variabile, e quindi si ottiene che
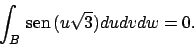
Soluzione 6.29 -
Notiamo che l'insieme di integrazione è invariante per rotazioni
intorno all'asse 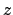 ; seguendo la discussione del punto
precedente, cerchiamo una rotazione dello spazio in modo che
il piano
; seguendo la discussione del punto
precedente, cerchiamo una rotazione dello spazio in modo che
il piano 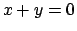 diventi nelle nuove coordinate
diventi nelle nuove coordinate 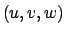 il piano
il piano 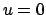 e consideriamo una rotazione che lasci inalterato
l'insieme di integrazione, cioè una rotazione effettuata attorno
all'asse
e consideriamo una rotazione che lasci inalterato
l'insieme di integrazione, cioè una rotazione effettuata attorno
all'asse 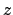 . Una tale rotazione è data ad esempio da
. Una tale rotazione è data ad esempio da
L'integrale diventa quindi
dove 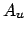 è l'area dell'ellisse
è l'area dell'ellisse
e ![$I_u=[-a,a]$](img225.png) . In definitiva troviamo che
. In definitiva troviamo che
Soluzione 6.30 -
Parametrizzando con le coordinate sferiche la superficie
con
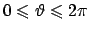 ,
,
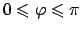 . Le derivate sono
. Le derivate sono
Il prodotto vettoriale è dato da
da cui
Quindi se 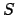 è la sfera l'area è
è la sfera l'area è
Soluzione 6.31 -
La superficie 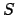 può essere vista come il grafico della funzione
può essere vista come il grafico della funzione
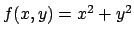 definita nel dominio
definita nel dominio
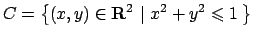 (si veda la Figura 6.11).
(si veda la Figura 6.11).
Figura 6.11:
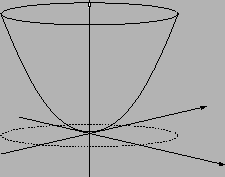 |
L'integrale diventa
che trasformato in coordinate polari diventa
Soluzione 6.32 -
L'integrale che si vuole calcolare è l'integrale della funzione
sulla superficie, data come grafico della funzione
sul dominio
Usando quindi la definizione di integrale superficiale, si ottiene
che
da cui
Soluzione 6.33 -
La superficie sulla quale si vuole calcolare l'integrale è dato
dal grafico della funzione
con
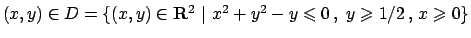 . Quindi otteniamo che
. Quindi otteniamo che
e l'integrale di superficie diventa quindi
Soluzione 6.34 -
Denotato con 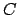 il cerchio di raggio
il cerchio di raggio 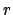 centrato nell'origine,
per il teorema della divergenza si ha
centrato nell'origine,
per il teorema della divergenza si ha
dove 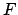 è un qualunque campo cha abbia divergenza
è un qualunque campo cha abbia divergenza 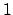 e
e 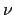 la normale esterna
al bordo di
la normale esterna
al bordo di 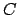 .
Si può prendere
.
Si può prendere
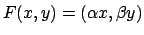 con
con
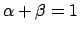 ,
l'esempio più semplice è prendere
,
l'esempio più semplice è prendere
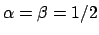 . Parametrizzando poi la
circonferenza con
. Parametrizzando poi la
circonferenza con
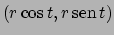 si ottiene
si ottiene
Soluzione 6.35 -
Per calcolare il flusso di tale campo si puó procedere in due modi, o
scrivendo l'integrale di superficie, oppure cercare di applicare il
Teorema della divergenza in  . Lasciamo il primo caso come esercizio
e vediamo come procedere nel secondo caso. Per poter applicare il Teorema
dalla divergenza dobbiamo avere a che fare con superfici
chiuse, quindi, siccome nel nostro caso abbiamo solo l'emisfero
superiore
. Lasciamo il primo caso come esercizio
e vediamo come procedere nel secondo caso. Per poter applicare il Teorema
dalla divergenza dobbiamo avere a che fare con superfici
chiuse, quindi, siccome nel nostro caso abbiamo solo l'emisfero
superiore 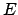 della sfera
della sfera
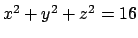 , dobbiamo
prima di tutto chiudere tale superficie; il modo
più semplice per fare ciò è considerare
l'insieme
, dobbiamo
prima di tutto chiudere tale superficie; il modo
più semplice per fare ciò è considerare
l'insieme
A questo punto abbiamo che, se
allora
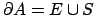 e quindi
e quindi
Quindi, dato che
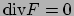 ,
,
Ma su 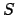 si ha che
si ha che
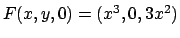 ,
,
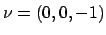 e
e 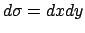 , quindi
, quindi
in definitiva abbiamo trovato che
Soluzione 6.36 -
Utilizzando il Teorema della divergenza, tenendo presente che
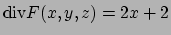 , otteniamo che
, otteniamo che
Per controllare che tale risultato sia giusto, si potrebbe calcolare
l'integrale di superficie del campo vettoriale 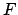 .
.
Soluzione 6.37 -
Notiamo anzitutto che il campo dato ha la proprietà
che
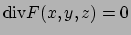 per ogni
per ogni
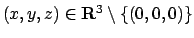 .
Questo vuol dire che se
.
Questo vuol dire che se 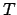 è un qualsiasi dominio
che non contiene l'origine, si ha che
è un qualsiasi dominio
che non contiene l'origine, si ha che
A questo punto, se
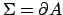 è una qualsiasi superficie
chiusa che contiene al suo interno l'origine, non possiamo
concludere che il flusso sia nullo in quanto la singolarità
del campo
è una qualsiasi superficie
chiusa che contiene al suo interno l'origine, non possiamo
concludere che il flusso sia nullo in quanto la singolarità
del campo 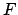 cade proprio nella porzione di spazio
racchiusa dalla superficie
cade proprio nella porzione di spazio
racchiusa dalla superficie 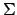 . Siccome l'origine
è un punto interno a
. Siccome l'origine
è un punto interno a 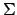 , esisterà un raggio
, esisterà un raggio 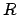 tale che la palla
tale che la palla 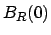 è tutta contenuta all'interno
di
è tutta contenuta all'interno
di 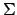 consideriamo quindi la porzione
di spazio
consideriamo quindi la porzione
di spazio
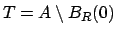 , abbiamo che
, abbiamo che
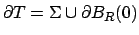 e a
questo punto l'origine non è più all'interno
di
e a
questo punto l'origine non è più all'interno
di 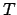 , quindi
, quindi
dove il segno meno nell'ultimo integrale tiene conto che 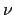 è la normale esterna alla palla
è la normale esterna alla palla 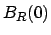 che però
rappresenta in tali punti la normale entrante nella regione
che però
rappresenta in tali punti la normale entrante nella regione 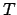 .
Quindi
.
Quindi
su
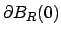 abbiamo che il campo si scrive
abbiamo che il campo si scrive
mentre la normale uscente da 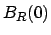 si scrive come
si scrive come
Per calcolare l'integrale utilizziamo le coordinate polari e
tenendo presente che
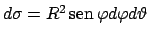 ,
otteniamo che
,
otteniamo che
Soluzione 6.38 -
Notiamo anzitutto che
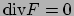 , quindi possiamo provare
ad applicare il Teorema della divergenza; per fare questo
dobbiamo considerare una superficie chiusa, dobbiamo
cioè chiudere la superficie data. Per fare questo possiamo
ad esempio considerare la superficie
, quindi possiamo provare
ad applicare il Teorema della divergenza; per fare questo
dobbiamo considerare una superficie chiusa, dobbiamo
cioè chiudere la superficie data. Per fare questo possiamo
ad esempio considerare la superficie
Se poniamo
abbiamo che
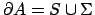 , e quindi dalla condizione
, e quindi dalla condizione
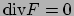 si ricava che
si ricava che
Ma su 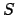 la normale uscente è data dal vettore
la normale uscente è data dal vettore 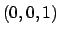 e
e 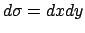 , quindi
, quindi



Next: About this document ...
Up: 6esercizi
Previous: 6esercizi
Fabio Paronetto
2005-06-22
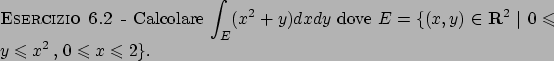
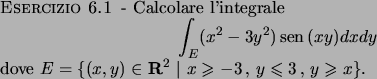
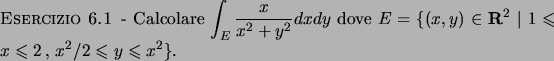
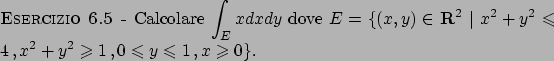
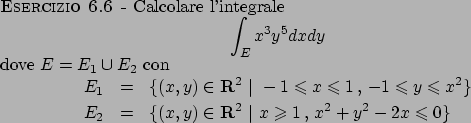
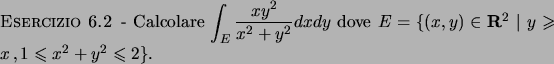
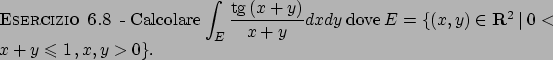
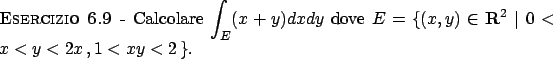
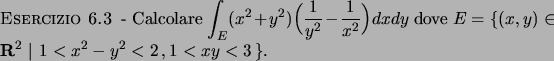
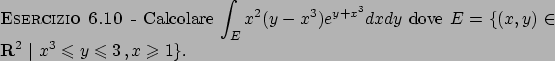
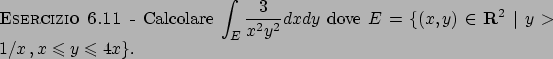
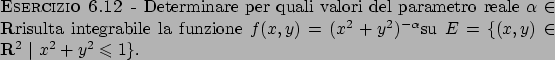
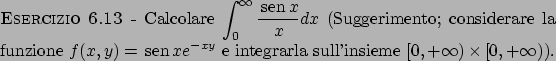
![\begin{esercizio}\rm -\
Calcolare l'area della regione $S$ compresa tra le curv...
...vartheta \in [-\pi/4,\pi/4].
\end{array}\right.
\end{displaymath}\end{esercizio}](img18.png)
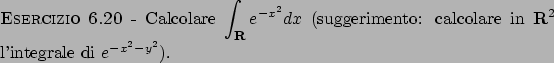

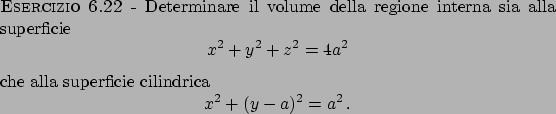
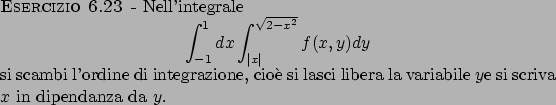
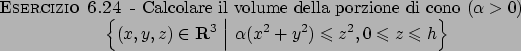
![]()
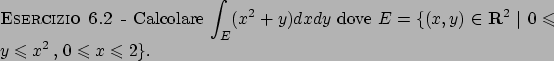
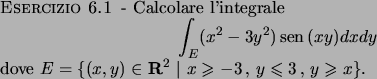
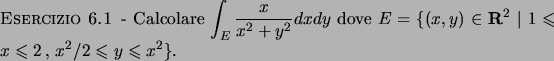
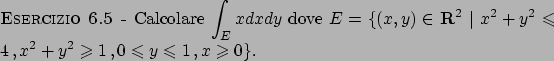
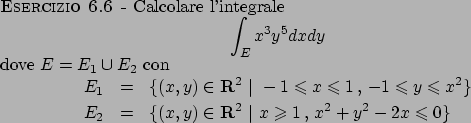
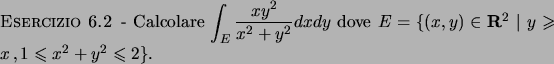
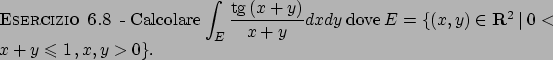
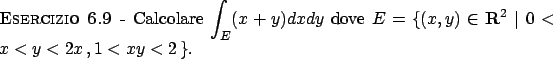
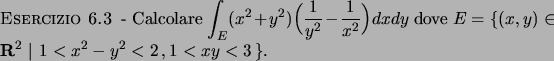
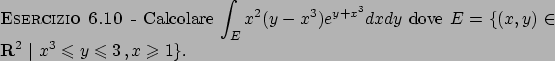
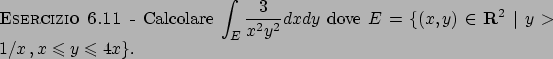
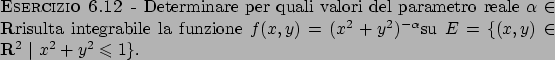
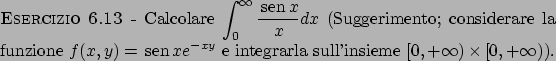
![\begin{esercizio}\rm -\
Calcolare l'area della regione $S$ compresa tra le curv...
...vartheta \in [-\pi/4,\pi/4].
\end{array}\right.
\end{displaymath}\end{esercizio}](img18.png)
![]()
![]()
![]()
![]()
![]()
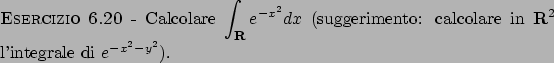

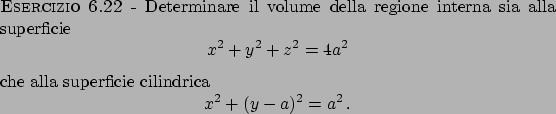
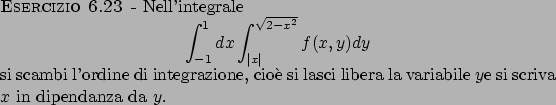
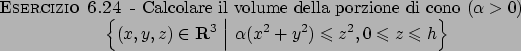
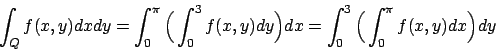
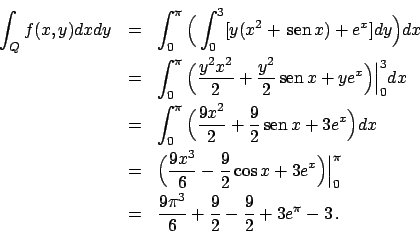
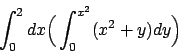
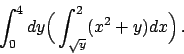
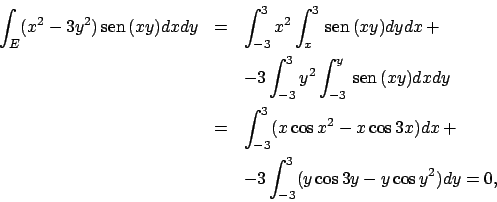
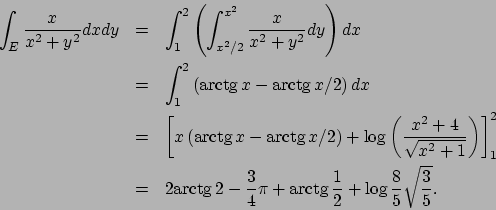
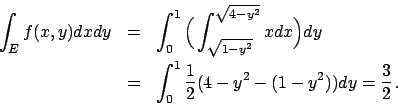
![\begin{eqnarray*}
\int _E \frac{xy^2}{x^2+y^2} dx dy &=&
\int _{[1,\sqrt{2}]\tim...
...\!^2\vartheta d\vartheta d\varrho \\
&=& \frac{\sqrt{2}-4}{18}.
\end{eqnarray*}](img61.png)
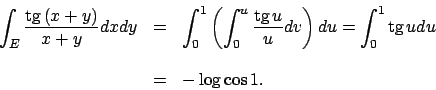

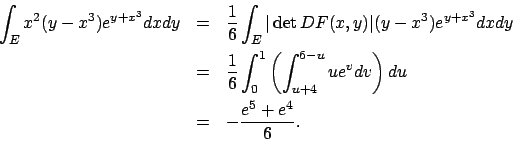


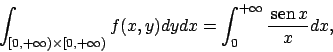
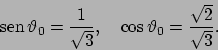
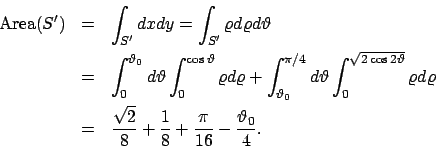
![\begin{displaymath}
\renewcommand {\arraystretch}{2}
\begin{array}{lll}
\textrm{...
...2}} \Big] dx } =
{\displaystyle {{1}\over{6}}} .
\end{array}\end{displaymath}](img124.png)
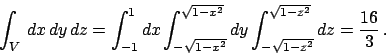
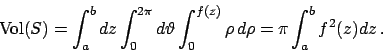
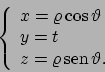
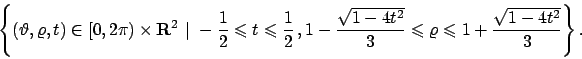
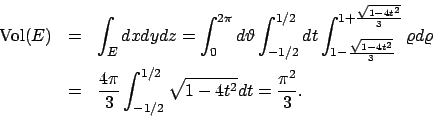
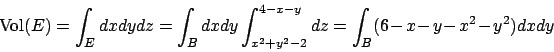
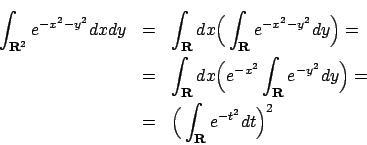
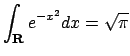 e più in generale
e più in generale

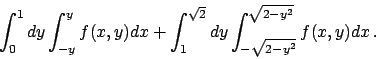
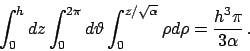
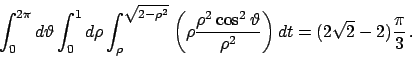
![]() è quello a sinistra in Figura 6.9.
Sicuramente l'integrale esiste perché la funzione integranda è limitata
e quindi
è quello a sinistra in Figura 6.9.
Sicuramente l'integrale esiste perché la funzione integranda è limitata
e quindi
![]() .
.
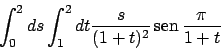
![]() ; particolari trasformazioni
con tale determinante sono le rotazioni, trasformazioni
che hanno il vantaggio nel nostro caso di trasformare la
palla
; particolari trasformazioni
con tale determinante sono le rotazioni, trasformazioni
che hanno il vantaggio nel nostro caso di trasformare la
palla ![]() centrata nell'origine e di raggio
centrata nell'origine e di raggio ![]() in se stessa.
Cerchiamo quindi una rotazione dello spazio che ad esempio mandi
il piano
in se stessa.
Cerchiamo quindi una rotazione dello spazio che ad esempio mandi
il piano ![]() nel piano determinato nelle nuove
coordinate
nel piano determinato nelle nuove
coordinate ![]() ad esempio da
ad esempio da ![]() . Una tale
rotazione è data ad esempio
. Una tale
rotazione è data ad esempio

![]() ; seguendo la discussione del punto
precedente, cerchiamo una rotazione dello spazio in modo che
il piano
; seguendo la discussione del punto
precedente, cerchiamo una rotazione dello spazio in modo che
il piano ![]() diventi nelle nuove coordinate
diventi nelle nuove coordinate ![]() il piano
il piano ![]() e consideriamo una rotazione che lasci inalterato
l'insieme di integrazione, cioè una rotazione effettuata attorno
all'asse
e consideriamo una rotazione che lasci inalterato
l'insieme di integrazione, cioè una rotazione effettuata attorno
all'asse ![]() . Una tale rotazione è data ad esempio da
. Una tale rotazione è data ad esempio da
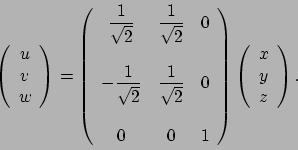
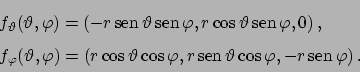
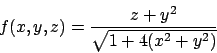
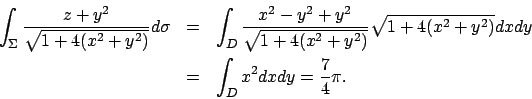
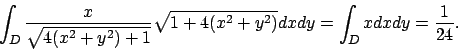
![]() il cerchio di raggio
il cerchio di raggio ![]() centrato nell'origine,
per il teorema della divergenza si ha
centrato nell'origine,
per il teorema della divergenza si ha
![]() . Lasciamo il primo caso come esercizio
e vediamo come procedere nel secondo caso. Per poter applicare il Teorema
dalla divergenza dobbiamo avere a che fare con superfici
chiuse, quindi, siccome nel nostro caso abbiamo solo l'emisfero
superiore
. Lasciamo il primo caso come esercizio
e vediamo come procedere nel secondo caso. Per poter applicare il Teorema
dalla divergenza dobbiamo avere a che fare con superfici
chiuse, quindi, siccome nel nostro caso abbiamo solo l'emisfero
superiore ![]() della sfera
della sfera
![]() , dobbiamo
prima di tutto chiudere tale superficie; il modo
più semplice per fare ciò è considerare
l'insieme
, dobbiamo
prima di tutto chiudere tale superficie; il modo
più semplice per fare ciò è considerare
l'insieme
![]() , otteniamo che
, otteniamo che
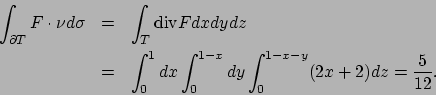
![]() per ogni
per ogni
![]() .
Questo vuol dire che se
.
Questo vuol dire che se ![]() è un qualsiasi dominio
che non contiene l'origine, si ha che
è un qualsiasi dominio
che non contiene l'origine, si ha che
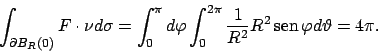
![]() , quindi possiamo provare
ad applicare il Teorema della divergenza; per fare questo
dobbiamo considerare una superficie chiusa, dobbiamo
cioè chiudere la superficie data. Per fare questo possiamo
ad esempio considerare la superficie
, quindi possiamo provare
ad applicare il Teorema della divergenza; per fare questo
dobbiamo considerare una superficie chiusa, dobbiamo
cioè chiudere la superficie data. Per fare questo possiamo
ad esempio considerare la superficie