Reduced models and reconstruction schemes for Magnetic Particle Imaging (MPI) based on efficient data sampling along Lissajous curves.
Description and analytic study of the imaging operator in Magnetic Particle Imaging within the scientific network MathMPI.
Analysis of optimal interpolation nodes on Lissajous-Chebyshev varieties. Efficient implementation based on the fast Fourier transform.
Analysis and numerical implementation of spectral interpolation methods for sampling nodes along rhodonea curves in the unit disk and spherical Lissajous curves.

Study of kernels with a discontinuous scaling function for a shape-preserving interpolation of an image with known and unknown edges.
Accelerated Landweber methods based on the usage of co-dilated orthogonal polynomials
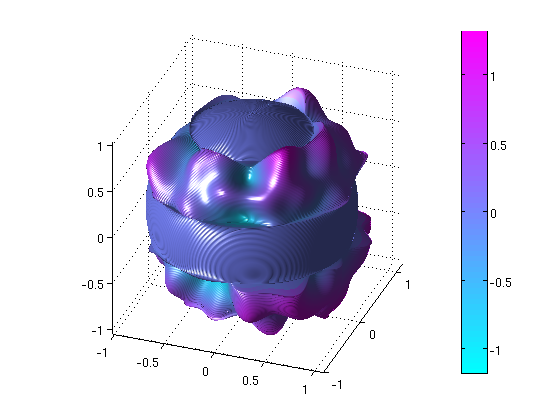
An analogue of the Landau-Pollak-Slepian time-frequency analysis for orthogonal polynomials on the real line and for spherical harmonics.

Uncertainty principles on manifolds and on graphs based on the mutual correlation between a space and a frequency localization operator.
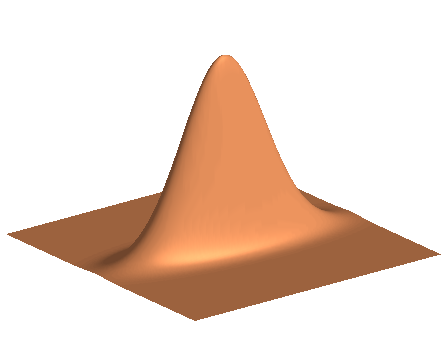
N-term approximation based on anisotropic gaussians has the same approximation power as N-term approximation with curvelets.

Kernel-based methods for interpolation, regression and classification on graphs. The kernels are generated by the generalized shifts of a principal graph basis function.
1. Magnetic Particle Imaging (MPI) and reconstruction on Lissajous curves
Magnetic Particle Imaging (MPI) is a novel biomedical imaging modality in which the
spatial distribution of superparamagnetic nanoparticles is determined by the non-linear magnetization response of the
particles to an applied magnetic field. These applied magnetic fields are usually generated in such a way that the signal acquisition is carried
out along a closed Lissajous curve.
This raises the natural question how a continuous function or discretized data values
along Lissajous trajectories can be extended into the surrounding region. Further, in MPI usually only a finite number of
Fourier coefficients of the signal on the acquisition trajectory are measured. This leads directly to the fascinating
mathematical question how a multivariate density function can be approximately recovered from limited spectral data on a curve.
In 2014, I initiated with several colleagues from different universities and industry the DFG-funded interdisciplanary scientific network
"Development, analysis and application of mathematical methods for Magnetic Particle Imaging (MathMPI) "
in which mathematical questions related to the imaging modality MPI are tackled.
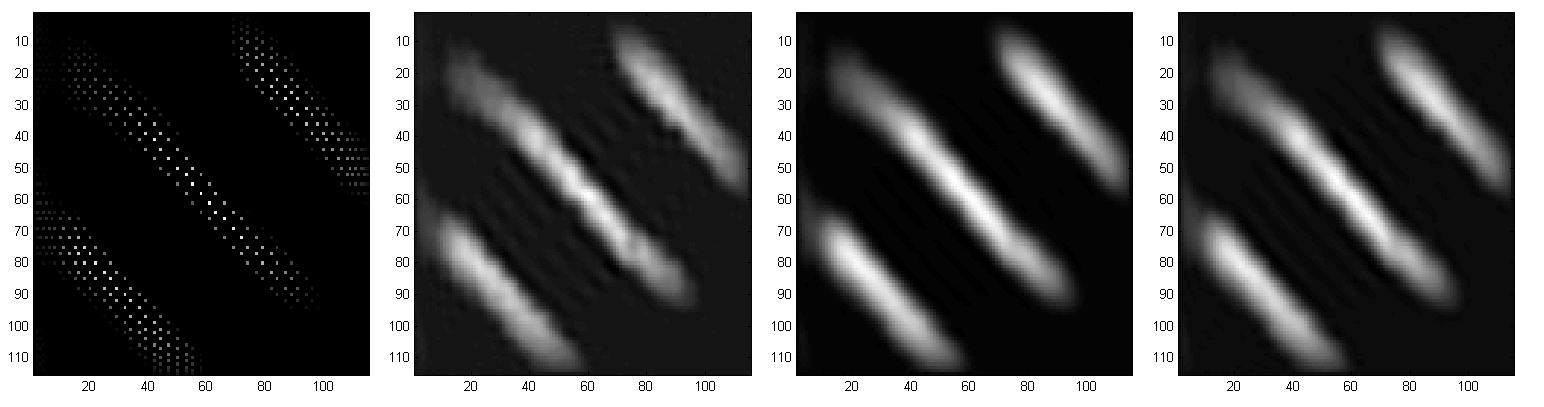
Fig. 1: Reconstruction of magnetic particle distributions based on Chebyshev spectral methods for data measured along Lissajous curves. Left: Particle density reconstructed on Lissajous node points. Middle left: Chebyshev reconstruction without filtering. Middle right: Chebyshev reconstruction with classical spectral filtering. Right: Chebyshev reconstruction with adaptive spectral filtering.
In the framework of this network we systematically studied mathematical questions related to the structure of Lissajous curves, its discretizations
and the interpolation and approximation of data along these trajectories. Similar as in the theory of the Padua points, we developed a
Chebyshev spectral method for an efficient polynomial interpolation on the node points of two- and higher dimensional Lissajous curves and applied them for
the reconstruction in MPI. In particular, we studied Lissajous node points as a possibility to reduce MPI measurements and to obtain efficient and fast
reconstructions at the same time. A second focus of research is the development of spectral basis elements such that the MPI system matrix can
be represented and stored in a sparse way. A third goal is the construction of adaptive spectral filters in order to improve the reconstruction quality
of the Chebyshev spectral methods.
This research was done in collaboration with the Institute of Medical Engineering at the University of Lübeck and the Institute of Biomedical Imaging at the UKE in Hamburg.
The adaptive spectral filters were developed in collaboration with the Padova-Verona research group on Constructive Approximation and Applications.
Publications
- Erb, W., Kaethner, C., Ahlborg, M. and Buzug, T.M. Bivariate Lagrange interpolation at the node points of non-degenerate Lissajous curves Numer. Math. 133, 4 (2016), 685-705 (Preprint)
- Erb, W., Kaethner, C., Dencker, P. and Ahlborg, M. A survey on bivariate Lagrange interpolation on Lissajous nodes Dolomites Research Notes on Approximation 8 (Special issue) (2015), 23-36 (Publication)
- Kaethner, C., Erb, W., Ahlborg, M., Szwargulski, P., Knopp, T. and Buzug, T. M. Non-Equispaced System Matrix Acquisition for Magnetic Particle Imaging based on Lissajous Node Points IEEE Transactions on Medical Imaging 35, 11 (2016), 2476-2485
- Schmiester, L., Moddel, M., Erb, W. and Knopp, T. Direct Image Reconstruction of Lissajous Type Magnetic Particle Imaging Data using Chebyshev-based Matrix Compression IEEE Transactions on Computational Imaging 3, 4 (2017), 671-681
- De Marchi, S., Erb, W. and Marchetti, F. Spectral filtering for the reduction of the Gibbs phenomenon for polynomial approximation methods on Lissajous curves with applications in MPI Dolomites Res. Notes Approx. 10 (2017), 128-137 (Publication)
2. Mathematical models in magnetic particle imaging
The modeling and the analysis of the imaging process in magnetic particle imaging is an ongoing research project within the research network MathMPI. In this project, we systematically investigate the continuous MPI imaging operator in different mathematical setups. As underlying function spaces for the analysis we introduce suitable Hilbert spaces and decompose the MPI imaging operator into simple building blocks. These suboperations are then analyzed with respect to their mathematical properties. In this way, we could obtain a complete analysis of the continuous 1D-MPI forward operator and, in particular, a mathematical description of it's ill-posedness. Further, we could show an exponential decay of the singular values of the 1D-MPI operator. In the 3D imaging setting, we developed a model-based reconstruction approach that incorporates realistic magnetic field topologies in terms of expansions in spherical harmonics.
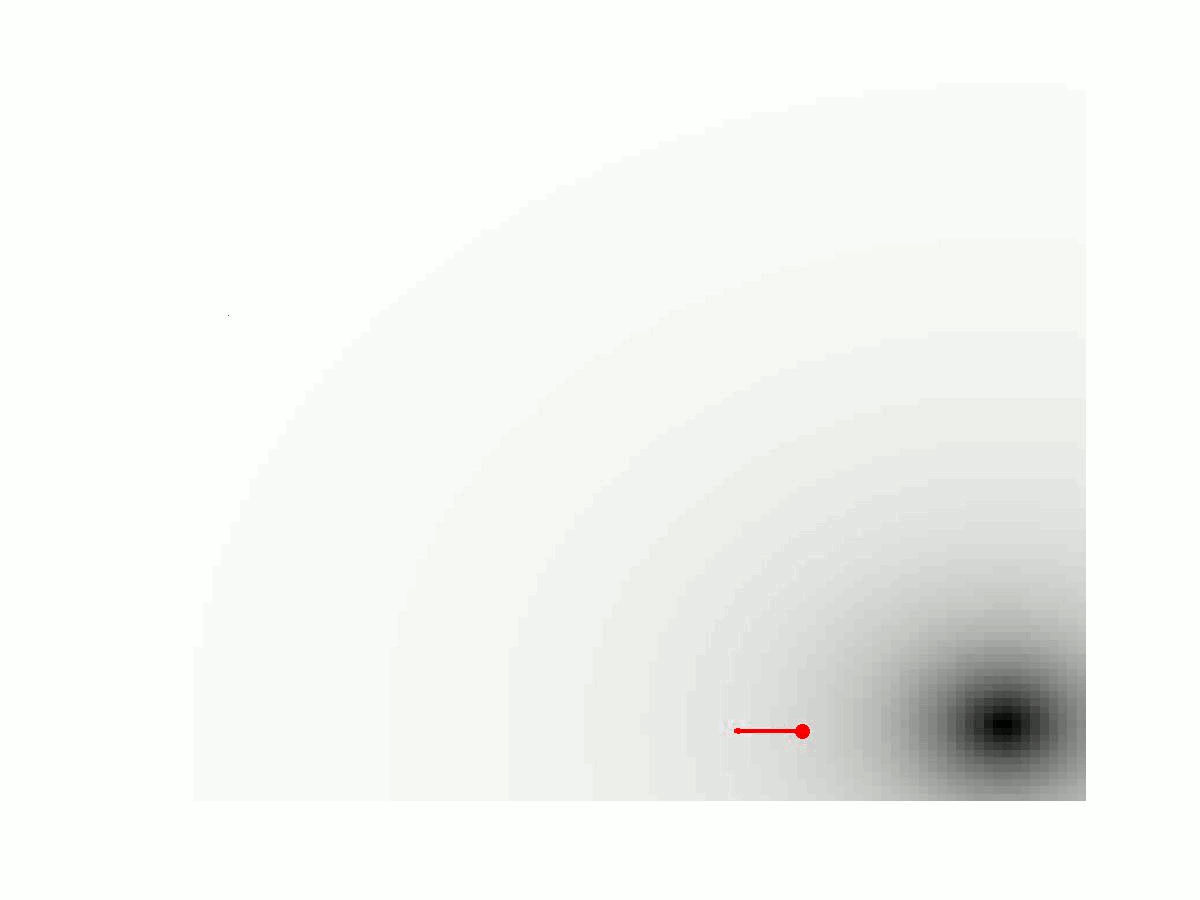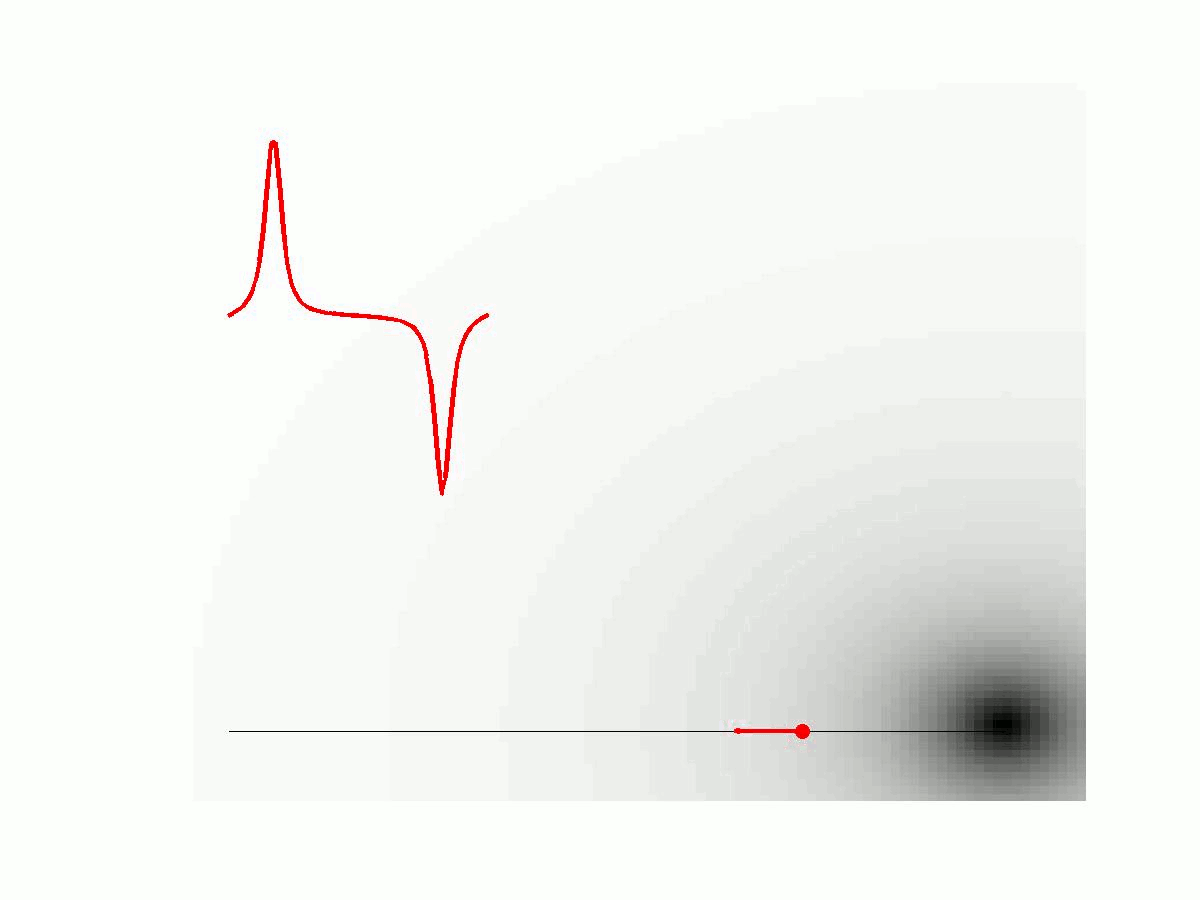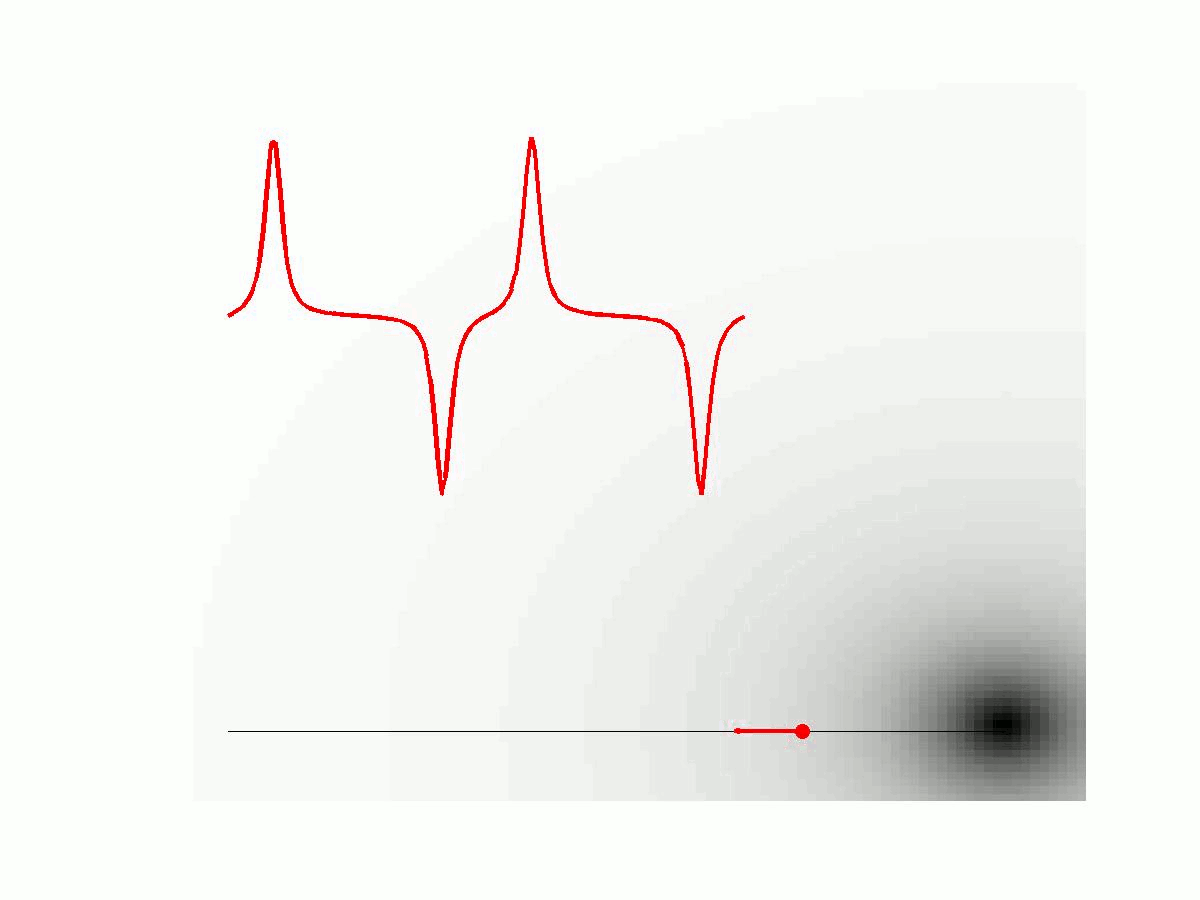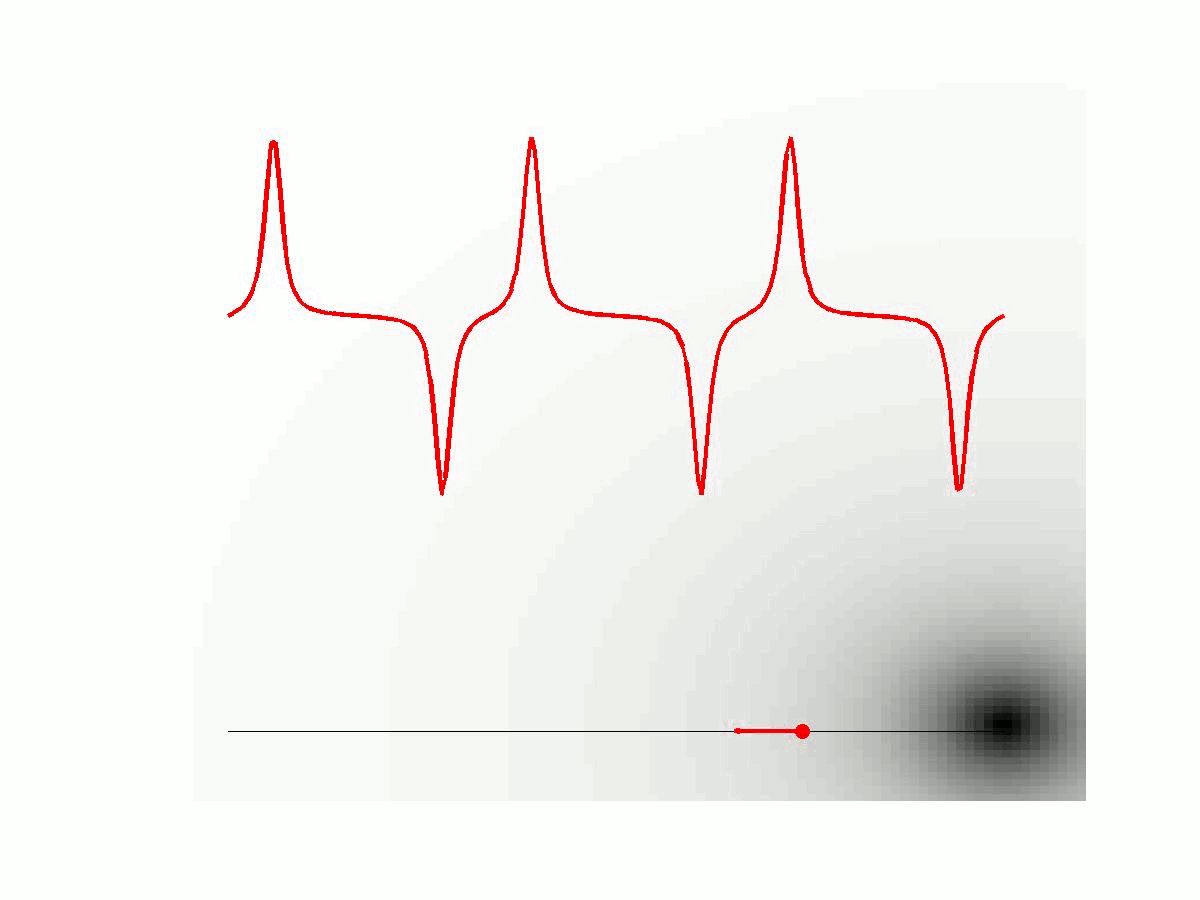
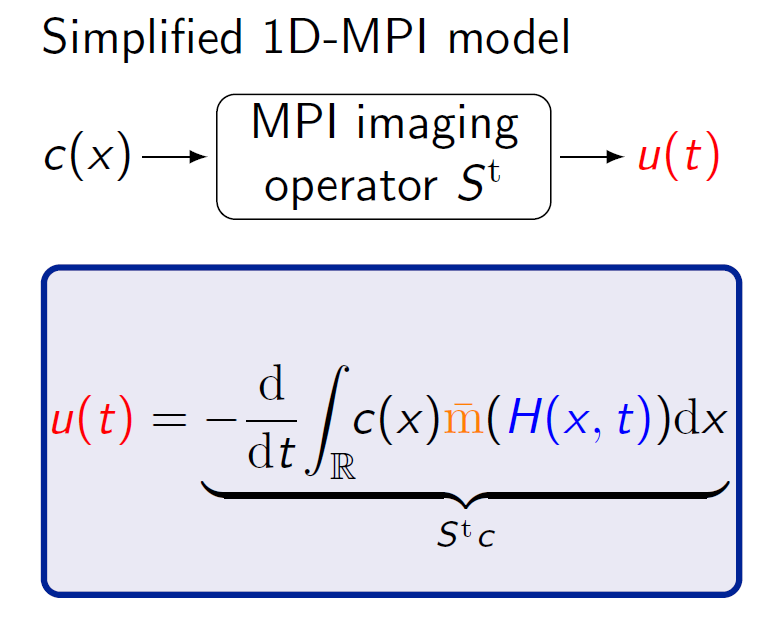
Formula 1: Simulation of the MPI signal generation process in 1D. The concentration c(x) of particles given here is a delta sample indicated by a red dot. The additional small arrow displays the magnetization of the particle in the external magnetic field. The moving low field region (the field free point) of the external magnetic field is illustrated with a black dot. The generated voltage signal u(t) is shown as a red curve. On the right hand side the corresponding MPI imaging equation is formulated as an integral equation.
Publications
- Bringout, G., Erb, W. and Frikel, J. A new 3D model for magnetic particle imaging using realistic magnetic field topologies for algebraic reconstruction. Inverse Problems 36 (2020), 124002 (Preprint)
- Erb, W., Weinmann, A., Ahlborg, M., Brandt, C., Bringout, G. , Buzug, T.M, Frikel J., Kaethner, C., Knopp, T., März, T., Möddel, M., Storath, M. and Weber, A. Mathematical Analysis of the 1D Model and Reconstruction Schemes for Magnetic Particle Imaging Inverse Problems 34 (2018), 055012 (Preprint)
3. Polynomial interpolation schemes on Lissajous curves
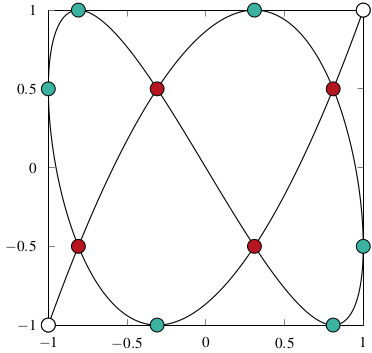
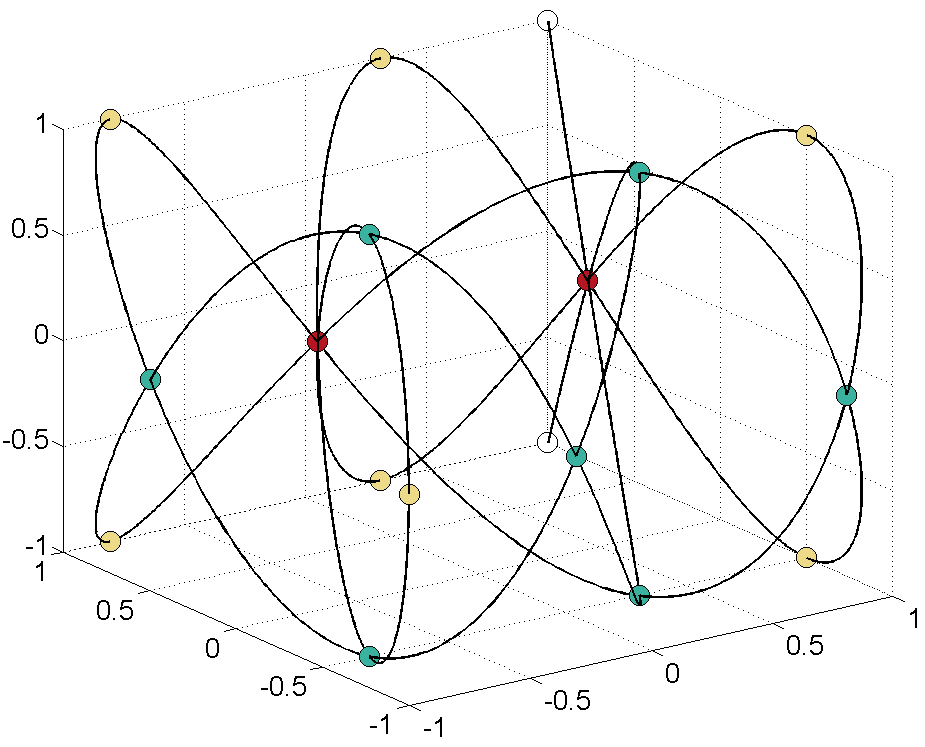
Fig. 2: Two Lissajous figures with the respective Lissajous-Chebyshev interpolation node points.
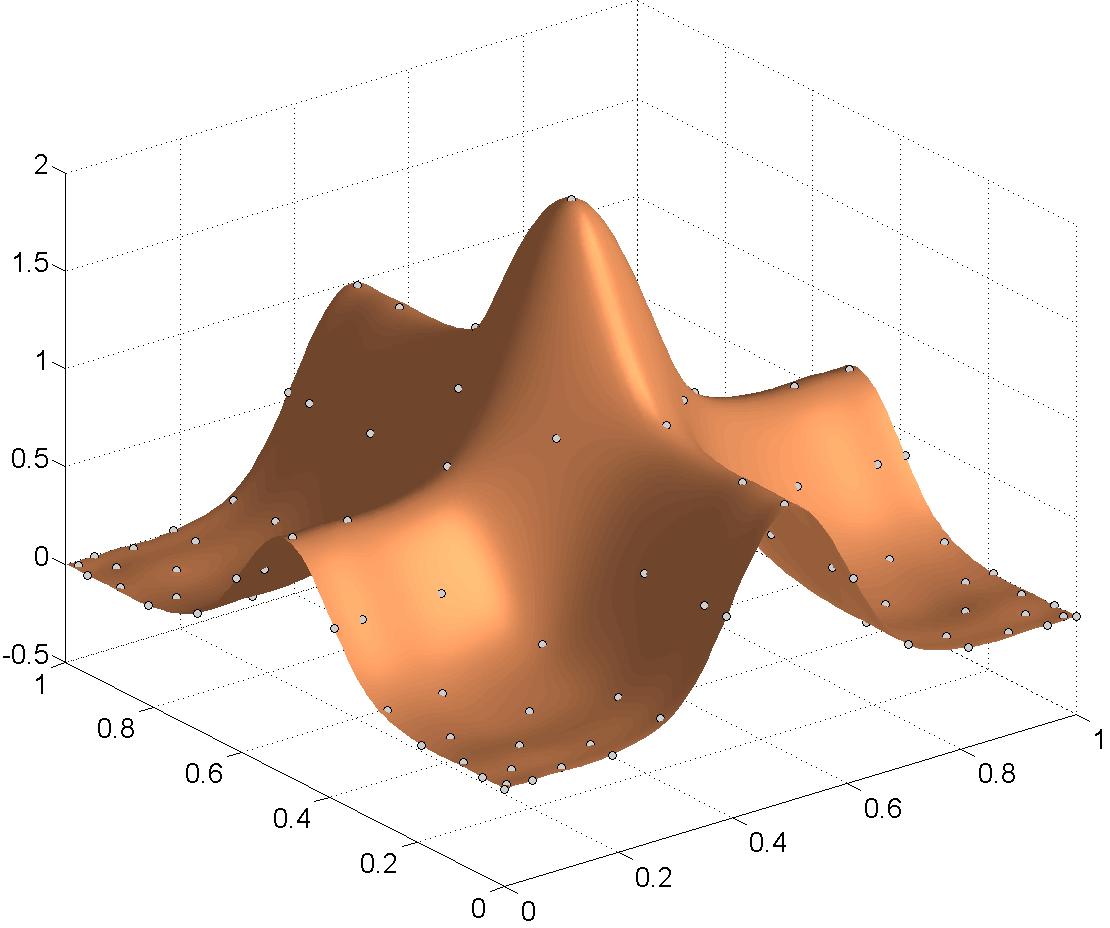
Starting from the applications in Magnetic Particle Imaging, I developed together with P. Dencker a comprehensive theory on multivariate polynomial interpolation related to Lissajous-Chebyshev points. This theory syntesizes and generalizes interpolation results for several well-known interpolation node sets as the Padua points, the Morrow-Patterson-Xu points or node points generated by a single Lissajous curve. We could show that these points give rise to a multivariate Chebyshev spectral interpolation scheme with some remarkable properties that can be implemented as efficiently as a tensor-product Chebyshev interpolant. Further, also the numerical condition and the convergence rates of the developed scheme are equivalent to the rates of a corresponding tensor-product Chebyshev scheme.

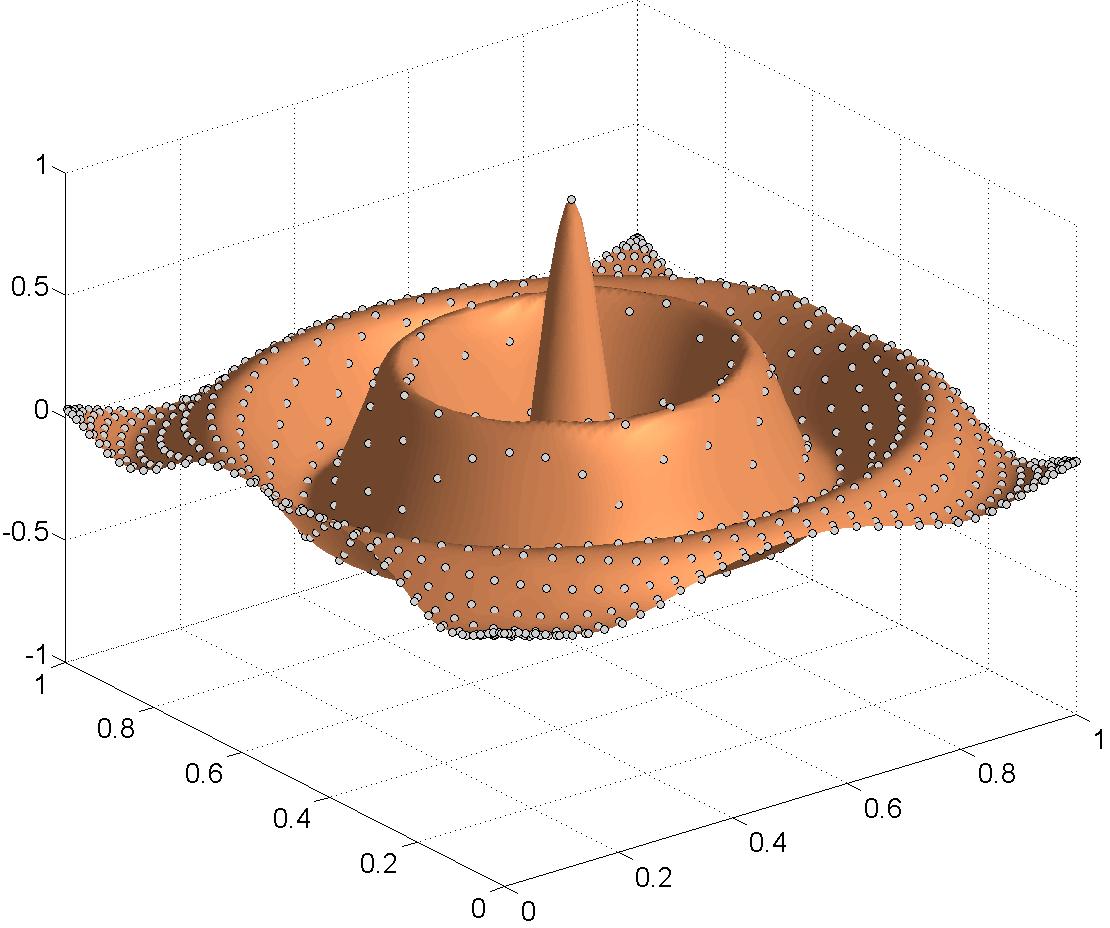
Fig. 3: Two polynomial interpolants of function values on Lissajous-Chebyshev points.
Publications
- Erb, W., Kaethner, C., Ahlborg, M. and Buzug, T.M. Bivariate Lagrange interpolation at the node points of non-degenerate Lissajous curves Numer. Math. 133, 4 (2016), 685-705 (Preprint)
- Erb, W. Bivariate Lagrange interpolation at the node points of Lissajous curves - the degenerate case Appl. Math. Comput. 289 (2016) 409-425 (Preprint)
- Erb, W., Kaethner, C. Dencker, P. and Ahlborg, M. A survey on bivariate Lagrange interpolation on Lissajous nodes Dolomites Research Notes on Approximation 8 (Special issue) (2015), 23-36 (Publication)
- Dencker, P. and Erb, W. Multivariate polynomial interpolation on Lissajous-Chebyshev nodes J. Approx. Theory, J. Approx. Theory 219 (2017), 15-45 (Preprint)
- Dencker, P., Erb, W., Kolomoitsev, Y. and Lomako, T. Lebesgue constants for polyhedral sets and polynomial interpolation on Lissajous-Chebyshev nodes Journal of Complexity 43, (2017), 1-27 (Preprint)
- Dencker, P. and Erb, W. A unifying theory for multivariate polynomial interpolation on general Lissajous-Chebyshev nodes arXiv:1711.00557 (2017) (Preprint)
Software
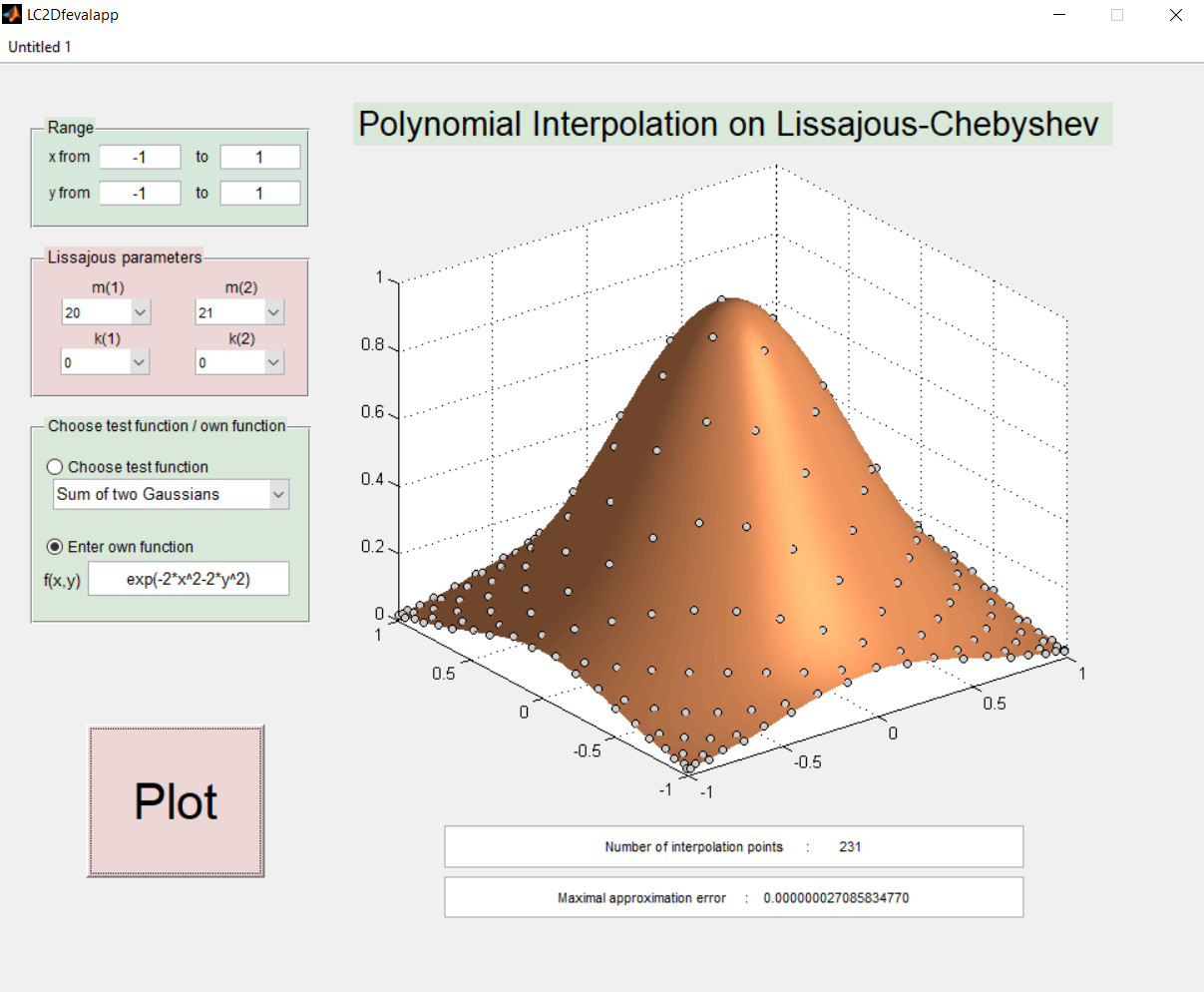
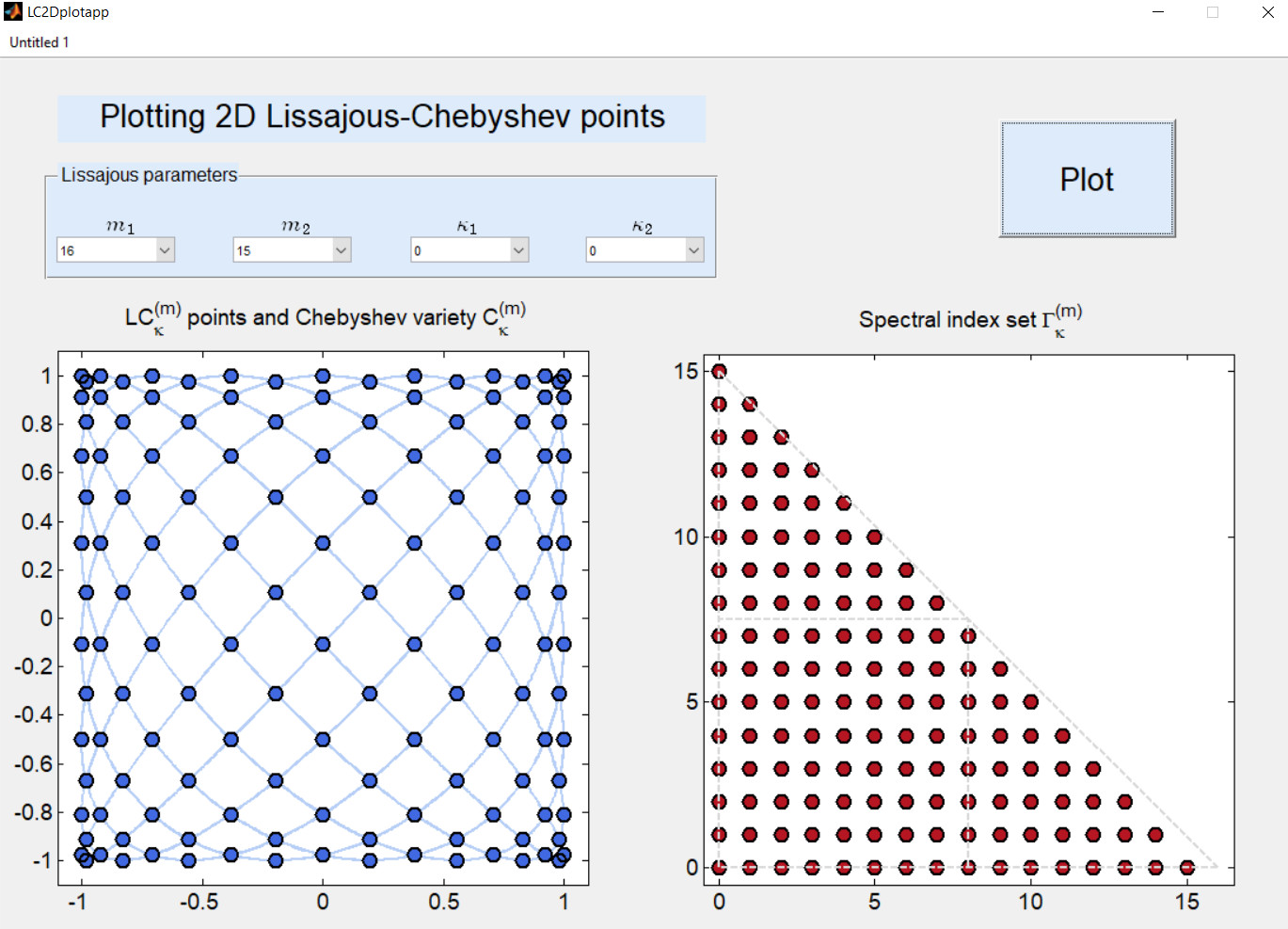
Fig. 4: The apps LC2Dfevalapp and LC2Dplotapp to test polynomial interpolation schemes on Lissajous-Chebyshev nodes.
- LC2Ditp: A software package that contains a Matlab implementation for 2D polynomial interpolation on general Lissajous-Chebyshev points. It contains also two apps to test the interpolation schemes (LC2Dfevalapp) and to display (LC2Dplotapp) the Lissajous-Chebyshev node points.
- LC3Ditp: A software package that contains a Matlab implementation for 3D polynomial interpolation on general Lissajous-Chebyshev points.
- LS2Ditp: This software package contains a Matlab implementation for bivariate polynomial interpolation on the node points of degenerate and non-degenerate 2D-Lissajous curves.
- LD3Ditp: A small software package that contains a Matlab implementation for 3D polynomial interpolation on the node points of degenerate 3D-Lissajous curves.
4. Spectral interpolation in spherical and polar geometries
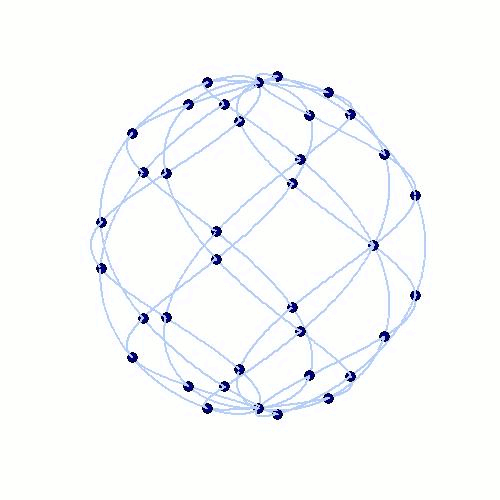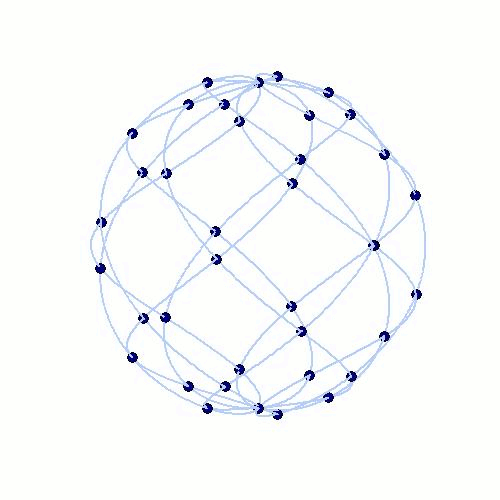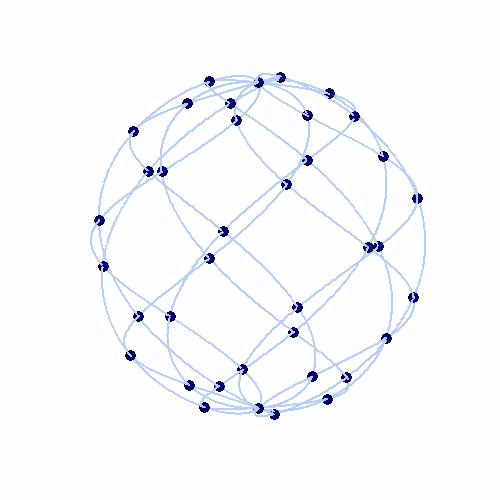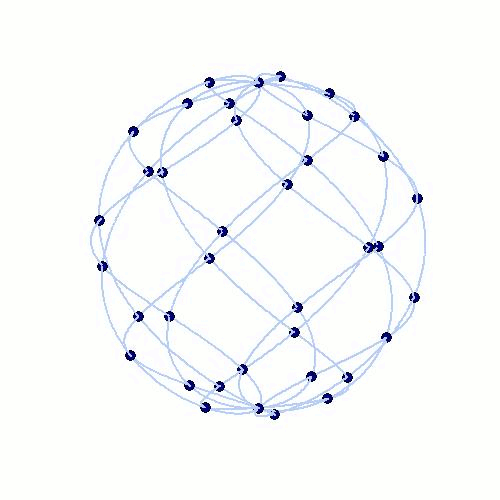
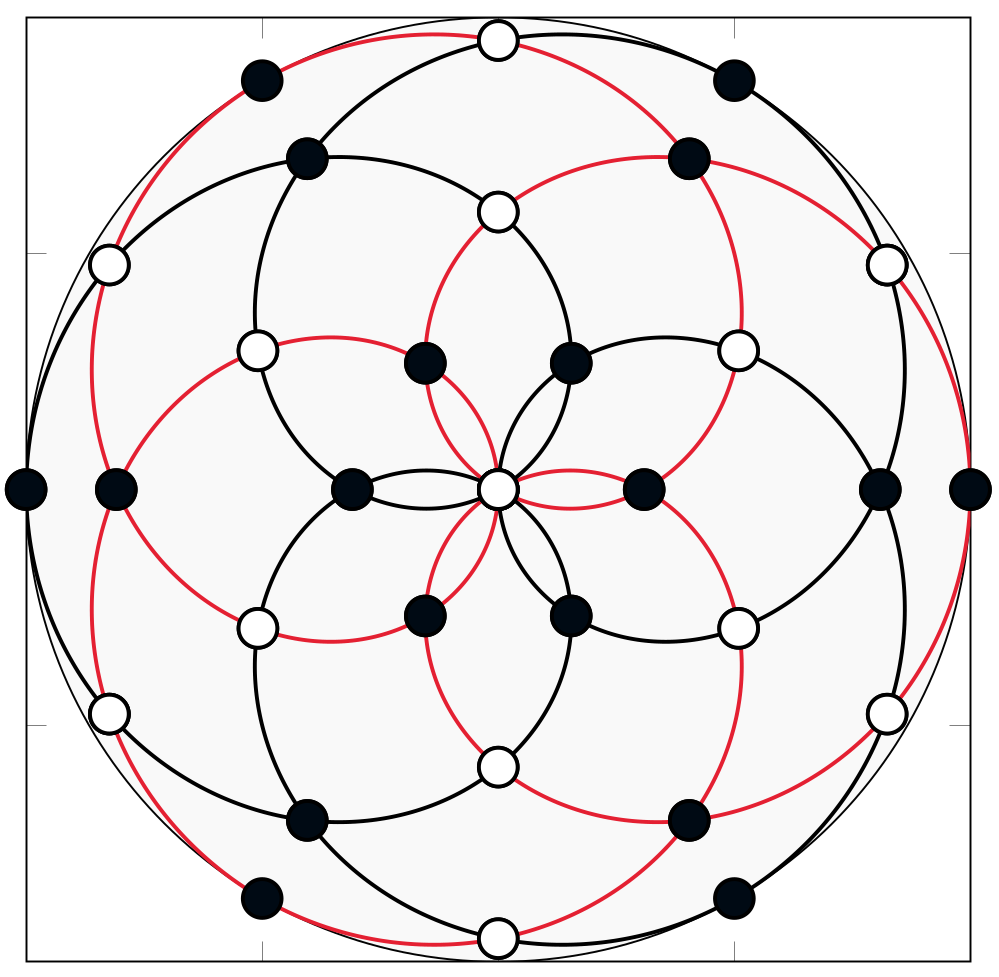
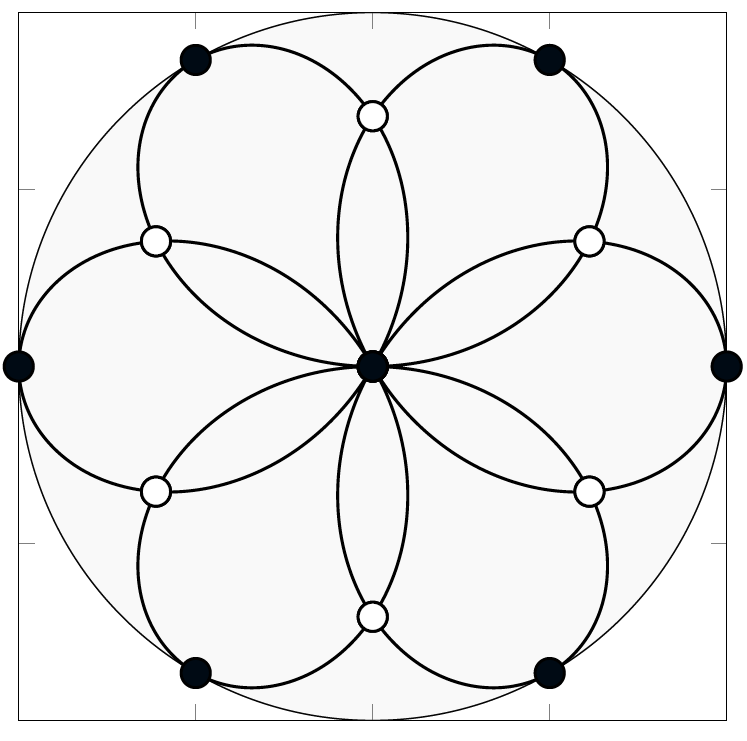
Fig. 5: The interpolation nodes of spherical Lissajous curves on the unit sphere (left) and of rhodonea curves on the disk (right).
Similar to the theory of polynomial interpolation on Lissajous-Chebyshev points, it is possible to derive interpolation schemes in spherical and polar coordinates. The generating curves in these geometries are spherical Lissajous curves on the unit sphere and the rhodonea curves on the unit disk. The corresponding interpolation spaces are not spanned by polynomials, but by parity-modified double Fourier series adapted to the underlying geometries. The resulting interpolation schemes can be implemented very efficiently by fast Fourier methods.
Software
- LSphere: This software package contains a Matlab implementation for spectral interpolation on the nodes of spherical Lissajous curves.
- RDisk: A software package that contains a Matlab implementation for spectral interpolation on the disk at the nodes of rhodonea curves.
Publications
- Erb, W. A spectral interpolation scheme on the unit sphere based on the nodes of spherical Lissajous curves. IMA J. Numer. Anal. 40:2 (2020), 1330–1355 (Preprint)
- Erb, W. Rhodonea curves as sampling trajectories for spectral interpolation on the unit disk. Constr. Approx. 53:2, 281-318 (2021) (Preprint)
5. Shape-driven interpolation with discontinuous kernels
If an image with sharp edges is interpolated by smooth basis functions, as for instance radial basis functions (RBFs) or polynomials, ringing artifacts appear close to the edges. These effects are commonly referred to as Gibbs phenomenon. In order to improve the resolution of discontinuities in the interpolation of scattered data sets, we studied the usage of variably scaled discontinuous kernels (VSDKs). For these discontinuous kernels, we obtained characterizations and theoretical Sobolev type error estimates for the native spaces. Further, we could show in experiments that in the presence of edges convergence is faster and Gibbs artifacts can be avoided if the VSDK interpolation scheme is used. By estimating unknown edges of an image with machine learning tools, this adaptive meshless method can be applied also as an interpolation tool in Magnetic Particle Imaging.






Fig. 6: Interpolation (upper right) with variably scaled discontinuous kernels of a painting of P. Mondrian (upper left) using image samples along a Lissajous curve (upper middle) and additional edge information for the three color channels (below).
Publications
- De Marchi, S., Erb, W., Marchetti, F., Perracchione, E. and Rossini, M. Shape-Driven Interpolation with Discontinuous Kernels: Error Analysis, Edge Extraction and Applications in MPI. SIAM J. Sci. Comput. 42:2 (2020), B472-B491 (Preprint) (Poster)
6. Iterative solvers for linear inverse problems
Linked to an interdisciplinary project in magnetic resonance elastography (MRE), I studied mathematical problems related to inverse problems in medical imaging. We
introduced and investigated accelerated Landweber methods for
linear ill-posed problems obtained by an alteration of the coefficients in the
three-term recurrence relation of the semi-iterative methods. The residual polynomials
of the methods under consideration are linked to a family of
co-dilated ultraspherical polynomials. This connection makes it possible to
control the decay of the residual polynomials at the origin by means of a
dilation parameter. Depending on the data, the approximation error of the
semi-iterative methods can be improved by altering this dilation parameter. The asymptotic convergence
order of the new semi-iterative methods turns out to be the same as for the original methods. We tested these new algorithms and developed a
simple adaptive scheme in which the dilation parameter is optimized in every iteration step.
In collaboration with Dr. Semenova these semi-iterative solvers were combined with adaptive discretization methods. We showed that
such an adaptive discretization approach in combination with a stopping criterion as the discrepancy
principle or the balancing principle yields an order optimal regularization scheme and allows
to reduce the computational costs.
Publications
- Erb, W. Accelerated Landweber methods based on co-dilated orthogonal polynomials Numer. Alg. 68, 2 (2015) 229-260
- Erb, W. and Semenova, E.V. On adaptive discretization schemes for the solution of ill-posed problems with semiiterative methods Appl. Anal. 94, 10 (2015) 2057-2076
7. Space-frequency analysis for orthogonal expansions
Based on the uncertainty principles constructed in my Ph.D. thesis, we developed a time-frequency theory for orthogonal
polynomials that runs parallel to the time-frequency
analysis of bandlimited functions developed by Landau, Pollak and Slepian. For this purpose, the spectral decomposition of a particular compact time-frequency-
operator is studied. This decomposition and its eigenvalues are
closely related to the theory of orthogonal polynomials. Results from both
theories, the theory of orthogonal polynomials and the Landau-Pollak-Slepian
theory, can be used to prove localization and approximation properties of the
corresponding eigenfunctions. Furthermore, an uncertainty principle was proven that
reflects the limitation of coupled time and frequency locatability.
In a second work, this theory was extended successfully to spherical polynomials on the sphere.
Using weak limits related to the structure of spherical harmonics provided us with information on the
proportion of basis functions needed to approximate localized functions. One big advantage of the developed theory
is the fact that the localized basis functions can be represented and computed efficiently with orthogonal polynomials.
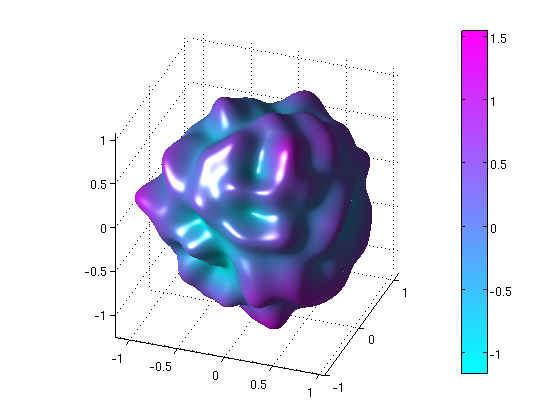
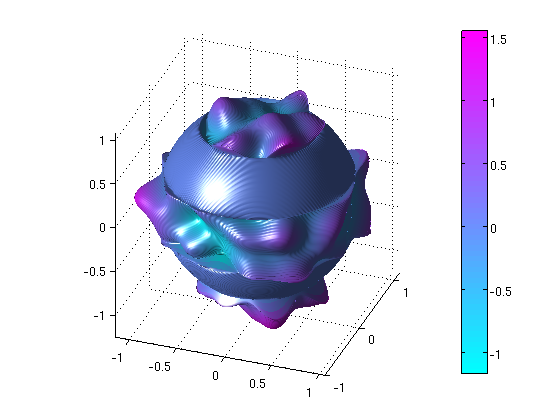

Fig. 7: Decomposition of a function on the unit sphere with localized polynomial basis functions.
Publications
- Erb, W. An orthogonal polynomial analogue of the Landau-Pollak-Slepian time-frequency analysis J. Approx. Theory 166 (2013) 56-77
- Erb, W. and Mathias, S. An alternative to Slepian functions on the unit sphere - A space-frequency analysis based on localized spherical polynomials Appl. Comput. Harmon. Anal. 38, 2 (2015) 222-241
8. Uncertainty principles on manifolds and graphs
Uncertainty principles form important theoretical cornerstones in signal analysis. They describe the inherent impossibility of a signal to be localized in space and frequency at the same time. Uncertainty relations can be formulated in a multitude of ways. The first uncertainty principle discovered by Heisenberg can for instance be written in terms of a commutator relation of a position with a momentum operator. In other contexts, uncertainty relations are described in terms of inequalities, by the space-frequency support or the smoothness of functions, or in form of boundary curves for an uncertainty region.
8.1. Uncertainty principles on Riemannian manifolds
As a PhD student, I was mainly interested in uncertainty principles on Riemannian manifolds. I showed that the product of a space and a frequency variance for functions on a Riemannian manifold is always larger than a particular constant. The key ingredient for the proof of this uncertainty principle is a commutator relation for particular Dunkl operators. In particular, these uncertainties turn out to be sharp. For 2-point homogeneous spaces, the space variance of the uncertainty product can be used to construct optimally space localized polynomials on symmetric spaces as the unit sphere.



Fig. 8: Illustrations of optimally space localized polynomials on the unit sphere in different spaces of spherical harmonics.
8.2. Uncertainty principles on graphs
The discrete harmonic structure in spectral graph theory allows to formulate uncertainty relations on graphs as well. The space and frequency localization of a graph signal in our general framework is measured in terms of suitable space and frequency filters. The resulting uncertainty relations can be characterized as the boundaries of an admissibility region and can be computed as the convex numerical range of a matrix.
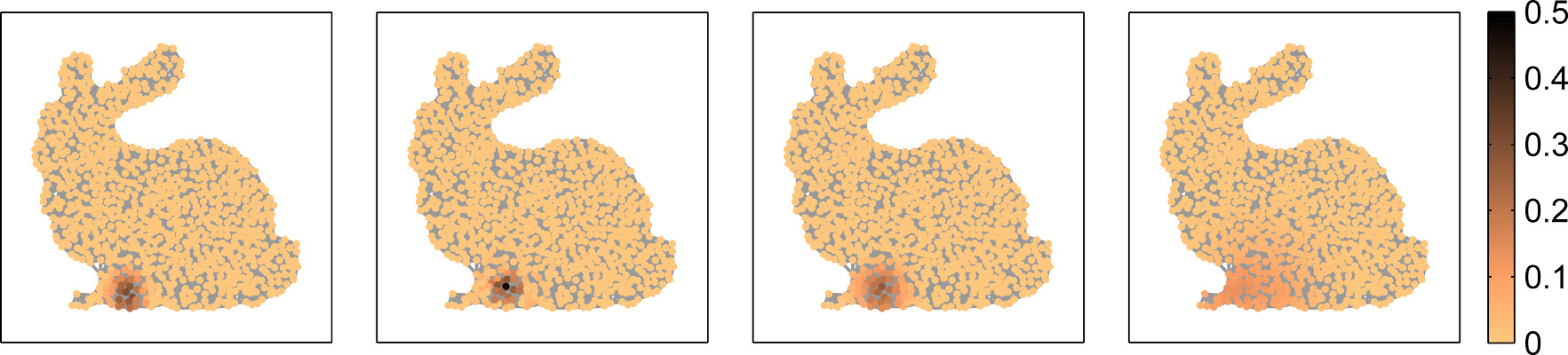
Fig. 9: Illustration of optimally space-frequency localized signals on a graph for different space-frequency filters generated with (GUPPY).
Publications
- Erb, W. Uncertainty principles on compact Riemannian manifolds Appl. Comput. Harmon. Anal. 29, 2 (2010) 182-197
- Erb, W. Uncertainty principles on Riemannian manifolds Logos Verlag Berlin (2010) Dissertation TU München
- Erb, W. Optimally space localized polynomials with applications in signal processing J. Fourier Anal. Appl. 18, 1 (2012) 45-66
- Erb, W. Shapes of Uncertainty in Spectral Graph Theory arXiv:1909.10865 (2019) (Preprint) (Software GUPPY)
9. Anisotropic approximation with gaussian mixtures
In this joint work with T. Hangelbroek and A. Ron, we showed that a representation system based on translated, dilated and rotated Gaussians yields essentially the same N-term approximation rate for cartoon class functions as a standard curvelet or shearlet system. The common construction principle for all these representation systems is to use one (or several) basic generating functions from which the entire system is generated by applying affine operations, as for instance the mentioned rotations, translations and dilations, to the generators. The idea of this work is to use adaptive Gaussian approximations of a given generator curvelet as new generating functions for a system of anisotropic Gaussian mixtures.
Publications
- Erb, W., Hangelbroek, T. and Ron, A. Anisotropic Gaussian approximation in $L_2(\mathbb{R}^2)$. arXiv:1910.10319 (2019) (Preprint)
10. Graph Interpolation and classification with graph basis functions (GBF's)
Graph basis functions (GBF's) are graph analogs of radial basis functions in the euclidean space and of spherical basis functions on the unit sphere. Linear combinations of generalized GBF shifts allow to approximate any signal on a graph. In this way, interpolation, regression and classification problems on graphs can be solved in a simple and efficient way. GBF's allow to include geometric information of the graph structure into these solutions and give simple characterizations of the involved approximation spaces in terms of the graph Fourier transform. Further, for kernel-based classification, GBF's offer a surprisingly simple possibility to construct feature-augmented kernels for semi-supervised learning on graphs. A more detailed introduction to graph basis functions can be found in this tutorial, or in the two publications below.
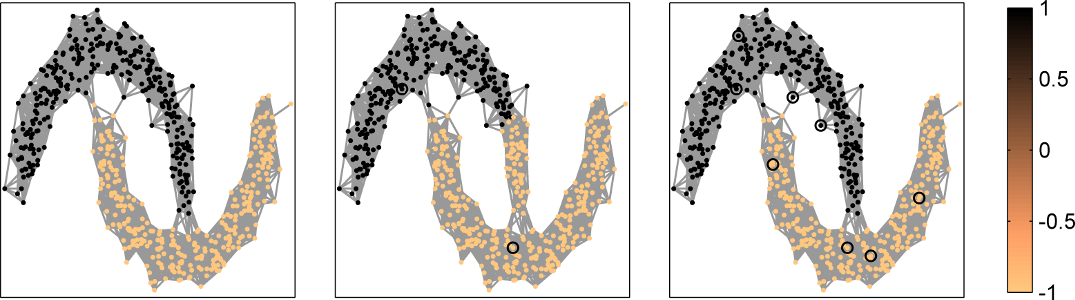
Fig. 10: Supervised classification of a two-moon data set (left) using a GBF regularized least squares method with 2 (middle) and 8 (right) labeled nodes (see implementation in GBFlearn).
Publications
- Erb, W. Graph Signal Interpolation with Positive Definite Graph Basis Functions. arXiv:1912.02069 (2019) (Preprint)
- Erb, W. Semi-Supervised Learning on Graphs with Feature-Augmented Graph Basis Functions. arXiv:2003.07646 (2020) (Preprint)
Software
- GBFlearn: A software package for the interpolation and classification of data on graphs with graph basis functions.
Further links
- CAA: Padova-Verona research group on "Constructive Approximation and Applications"
for further information and references on Padua points and polynomial approximation on Lissajous curves - Gruppo di lavoro UMI: Teoria dell'Approssimazione e Applicazioni - T.A.A., a working group on approximation theory and its applications.
- GNCS-INdAM, a working group on scientific computing at INdAM.
- The Institute of Biomedical Imaging at the UKE in Hamburg
- Mathematical methods for Magnetic Particle Imaging (MathMPI)
for further information on the DFG-funded interdisciplanary scientific network MathMPI - International Workshop on Mathematical Imaging and Emerging Modalities (MIEM2016),
27-30/06/2016 in Osnabrück, Germany - Have a look at the Portfolio of Elio A. Farina if you require professional latex typesetting
 University of Padova
University of Padova University of Hawaii
University of Hawaii University of Lübeck
University of Lübeck arXiv Preprints
arXiv Preprints ResearchGate
ResearchGate