The Partitioned Toy Example: Concurrency View
This part of the tutorial describes the application of the model transformation to the Partitioned Toy Example, introduced in section 3 and recalled in figure 8.5. Note that this example is different from the Distributed Toy Example which has been used in the previous sections. The main difference is that the system modeled in the Partitioned Toy Example is not distributed. The application of model transformation to the Distributed Toy Example is slightly more complex, and it is discussed separately
- Partition P1: POS and GNC;
- Partition P2: TMTC;
- Partition P3: PRO.
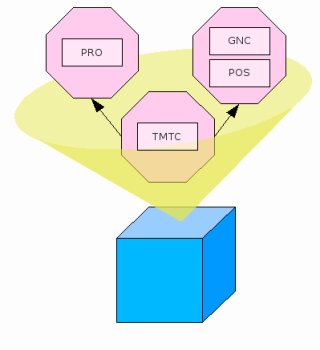
Figure 8.5: The Partitioned Toy Example
Partition P1: POS, GNC
POS APLC
As shown in Figure 5.2, the POS APLC has three elementary PI which are all of type immediate:
-
Read is private (in that in the Functional View it is not included in any public port cluster) and provides read-protected access rights to the functional state of POS.
-
Write provides mutual-exclusive access to the functional state of POS.
-
Read_X_Write is a composite operation (that is, one whose execution entails the invocation of at least one RI) with transactional access and thus holds mutually-exclusive access rights over the functional state of POS during its entire execution.
POS also has an elementary RI typed to the Compute operation of the GNC APLC. That elementary RI is attached to the Read_X_Write operation and it is thus attributed to the VMLC product of the transformation that includes Read_X_Write in its PI. The model transformation of POS places all elementary PI in one and the same group since all of them use the same set of variables. This group generates a single protected VMLC (shown in Figure 8.6) which thus realizes the whole POS APLC. The type of the resulting VMLC is determined by the grammar rules presented in [Var06, CV06].
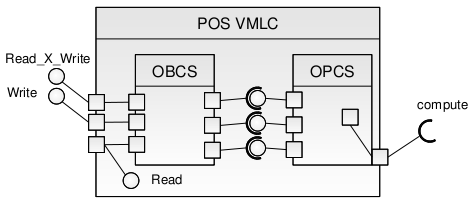
Figure 8.6: The POS VMLC
GNC APLC
The GNC APLC has two elementary PI as follows:
-
GNC_op, which is private and cyclic
-
Compute, which is public and unprotected
and one elementary RI whihc requires the Read_X_Write operation. Model transformation places those two elementary PI in two groups since their respective attributes make them incompatible.
Model transformation places those two elementary PI
of in two distinct groups since their respective attributes make them
incompatible. Each group (which in this case includes a single
elementary PI) generates one VMLC. A cyclic threaded VMLC realizes the
GNC op operation, whereas a passive VMLC realizes the Compute
operation. Since the GNC op operation exhibits a requirement for
the Read_X_Write RI, that elementary RI is attributed to the cyclic
threaded VMLC which provides the GNC_op operation. The result of the
transformation is shown in Figure 8.7
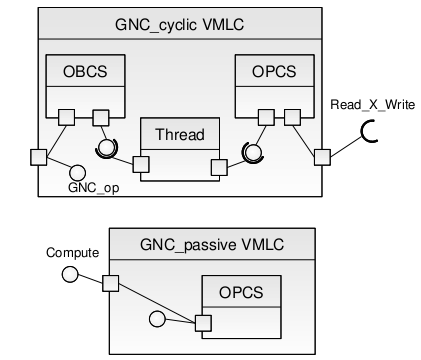
Figure 8.7: The GNC VMLC
Partition P2: TMTC
The TMTC APLC has two elementary PI as follows:
-
Dispatch, which is public and sporadic
-
Send, which is public and sporadic, too
and four elementary RI, typed POS_Writer and PRO_Boost, which emanate from the implementation of the Send and Dispatch operations, respectively. The RCM grammar states that an interface group can contain only one deferred elementary PI which is set to denote the nominal operation. Model transformation of the TMTC APLC places each individual elementary PI in a single interface group, which maps to a sporadic threaded VMLC where they denote the nominal operation of the thread embedded in the VMLC. As we have seen earlier, the PI of every VMLC that results from the transformation determines the RI of that VMLC in accord with what specified in the Functional View (and reflected in the Interface View). Figure 8.8 shows the sporadic threaded VMLC that results from the model transformation of the TMTC APLC for the part that realizes the Dispatch operation. Figure 8.9 zooms in the sporadic threaded VMLC which realizes the Send operation.
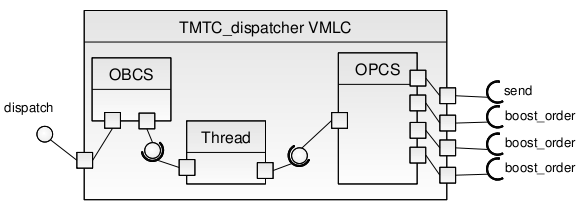
Figure 8.8: The sporadic threaded VMLC that realizes the Dispatch operation of the TMTC APLC
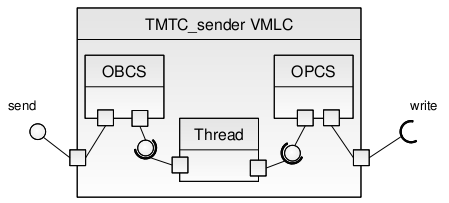
Figure 8.9: The sporadic threaded VMLC that realizes the Send operation of the TMTC APLC
Partition P3: PRO
The PRO APLC exhibits two elementary PI as follows:
-
Pro_OP, which is private and deferred, tagged nominal and cyclic
-
Boost_Order, which is public and deferred, tagged modifier to the nominal deferred behavior of the component.
The RCM grammar states that an interface group can contain only one nominal elementary PI and that group must also contain all of the modifiers specified to it. Therefore, model transformation of the PRO APLC places all elementary PI in one and the same interface group where Boost_Order is the modifier of the nominal cyclic elementary PI PRO_op. The PRO APLC is thus realized by a single cyclic threaded VMLC as shown in Figure 8.10.
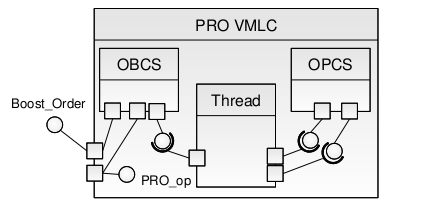
Figure 8.10: The PRO VMLC