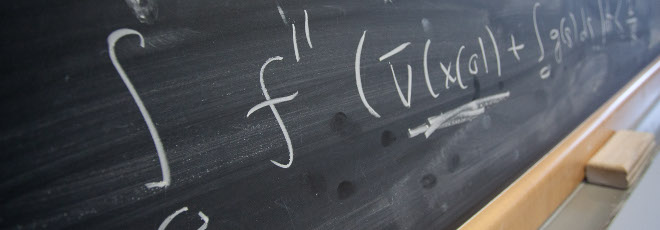
“The Grunwald Problem for solvable groups”
Martedì 4 Novembre 2025, ore 14:30 - Aula 2AB45 - Julian Demeio (Università di Hannover)
Abstract
Let $K$ be a number field. The Grunwald problem for a finite group (scheme) $G/K$ asks what is the closure of the image of $H^1(K,G) \to \prod_{v \in M_K} H^1(K_v,G)$. For a general $G$, there is a Brauer-Manin obstruction (BMO) to the problem, and this is conjectured to be the only one. In 2017, Harpaz and Wittenberg introduced a technique that managed to give a positive answer (BMO is the only one) for supersolvable groups. I will present a new fibration theorem over quasi-trivial tori that, combined with the approach of Harpaz and Wittenberg, gives a positive answer for all solvable groups.




