|
Questa pagina è dedicata al corso di Geometria 2 per il corso di Laurea in Matematica per l'anno accademico 2024/2025. Vi si troveranno file in formato pdf contenenti appunti ed esercizi relativi alle lezioni. Vi compariranno anche testi e risultati degli esami (dopo che saranno stati svolti). Il corso di Geometria 2 (14 crediti) si svolge nel primo semestre per 8 crediti (parte A) e nel secondo per 6 crediti (parte B); il docente responsabile sono io (Maurizio Cailotto, e qui siete nella mia home page). Durante i semestri si terranno delle prove scritte parziali. Alla fine del primo semestre si terra` un parziale della parte A. Alla fine del secondo semestre si terranno i due appelli scritti ufficiali (su tutto il programma) e le prove orali (obbligatorie per tutti e che verranno svolte su appuntamento in giorni fissati, una volta superate le parti scritte). Ulteriori appelli (scritti e orali) si terranno nelle sessioni di recupero (agosto e settembre). Ad ogni appello scritto lo studente puo` decidere se affrontare solo la parte A, solo la parte B, o entrambe. L'orale e` unico su tutto il programma; alla fine dell'orale viene proposto un voto complessivo che tiene conto dei voti sulle parti scritte A e B, e dell'orale stesso. |
|
Scopo del corso di Geometria 2 nel primo semestre è completare le conoscenze di Geometria 1, introducendo le nozioni fondamentali sugli oggetti geometrici di secondo grado (forme bilineari, quadratiche, coniche, quadriche). Gli strumenti introdotti e utilizzati rientrano nell'ambito dell'Algebra Lineare, e saranno usati in vari corsi (Analisi Matematica 2, corsi del terzo anno). Argomenti: - inizieremo con un ripasso di geometria proiettiva/affine/euclidea; - il primo argomento nuovo sara` lo studio delle forme bilineari e quadratiche, che generalizza e rende indipendente dalla base scelta la nozione di prodotto scalare; tutte le nozioni (ortogonalita`, decomposizioni e proiezioni ortogonali, basi ortogonali e ortonormali) saranno estese ad un ambiente piu` generale, in cui le funzioni non sono necessariamente definite positive [questi argomenti saranno poi usati in Analisi 2 per lo studio di massimi e minimi di funzioni di piu` variabili reali]. - il secondo argomento, geometria e classificazione di coniche e quadriche (gli oggetti piu` semplici dopo gli iperpiani: sono quelli definiti da equazioni di secondo grado) verra` svolto nelle geometrie proiettiva, affine, euclidea e sara` apprezzato solo avendo ottime basi per tutte, specie nel caso euclideo (si useranno matrici e riferimenti ortogonali per ottenere le equazioni canoniche e i vari invarianti: semiassi, fuochi,...). ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ Esempi: ballata delle due rette (proiezioni in piani affini diversi delle stesse due rette nel piano proiettivo) e ballata di una conica (perche' le coniche irriducibili affini sono proiettivamente equivalenti):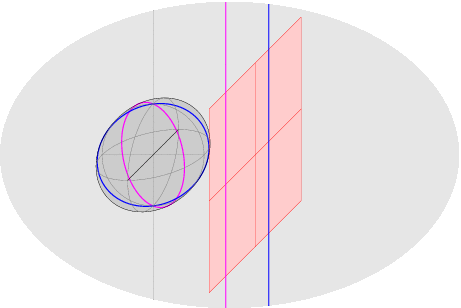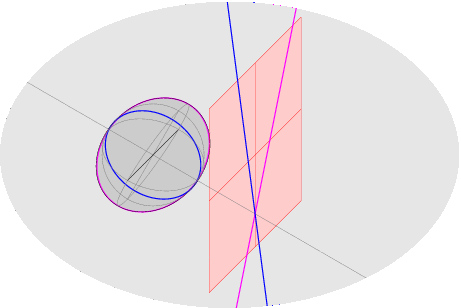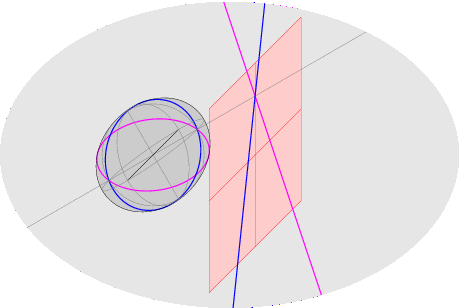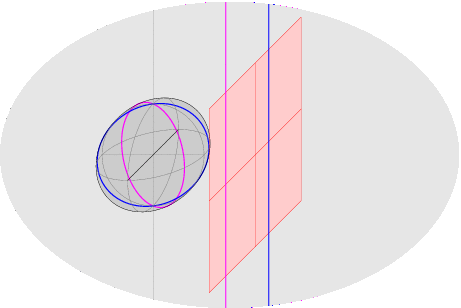 
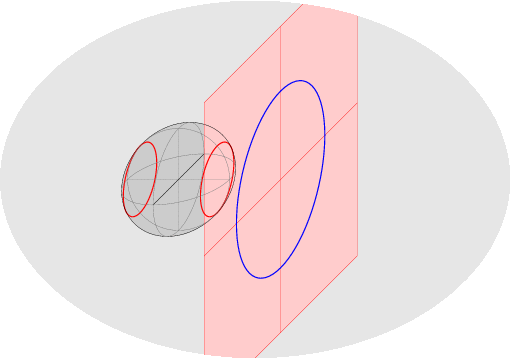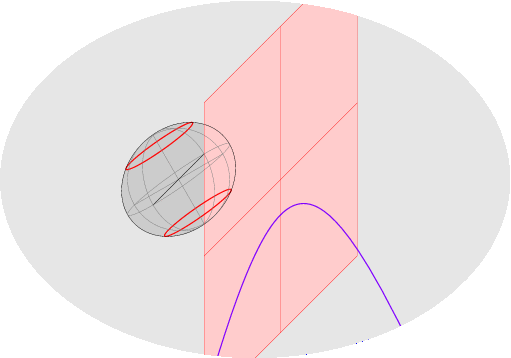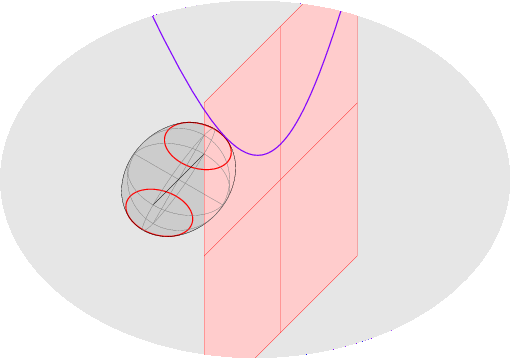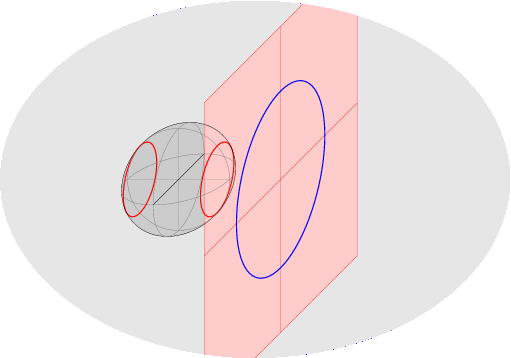
Altro esempio: la quadrica rigata immagine della mappa di Segre: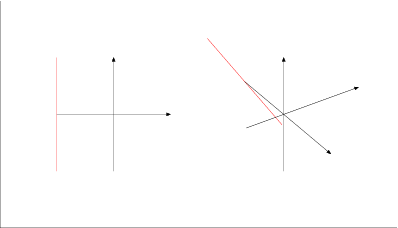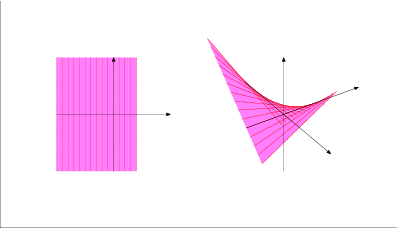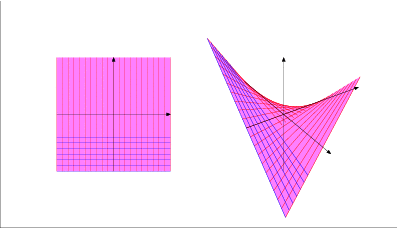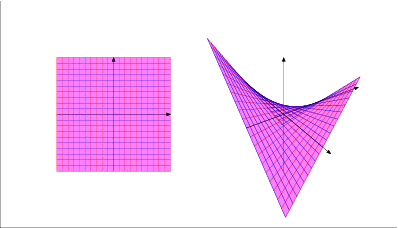 
|
|
Nel secondo semestre si studiera` la geometria differenziale delle curve e delle superficie, specie immerse nel piano e nello spazio; poi le nozioni elementari di topologia generale, in parte gia` incontrate nei corsi di analisi e geometria, finendo con la classificazione delle superficie reali compatte: - si inizia lo studio della geometria differenziale delle curve (lunghezza, curvatura, torsione, riferimenti ed equazioni di Frenet...), -e delle superficie immerse in R^3 (regolarita`, forme fondamentali, mappe di Gauss e Weingarten, curvature, teorema egregium, curve sulle superficie e geodetiche...). ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ Qualche curva classica: rotolando una circonferenza 
(il punto della circonferenza descrive un cicloide); rotolando una parabola qui (il fuoco descrive una catenaria); far rotolare una ellisse e` piu` complicato perche' il parametro d'arco non si esprime con funzioni elementari: qui. Far rotolare una iperbole e` piu` deludente (perche'?). Far rotolare una spirale logaritmica porta il centro a descrivere una retta (che interseca la tangente asintoticamente); che traiettoria descrivono i punti della spirale? Dopo aver provato a immaginarlo, si puo` vedere qui. Far rotolare una circonferenza lungo un'altra circonferenza da` luogo a epicicloidi (rotolamento esterno) o ipocicloidi (rotolamento interno); sono curve algebriche se il rapporto dei raggi delle due circonferenze e` razionale, per esempio: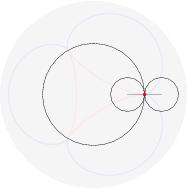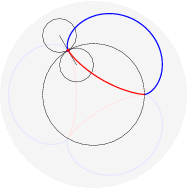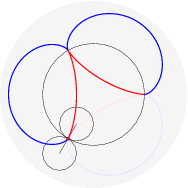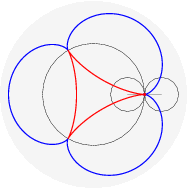 
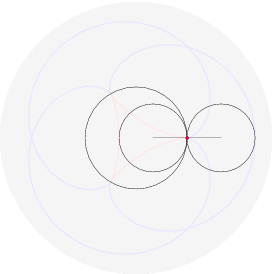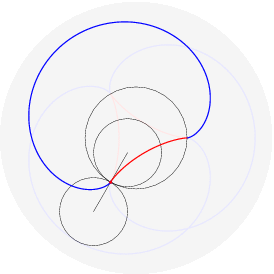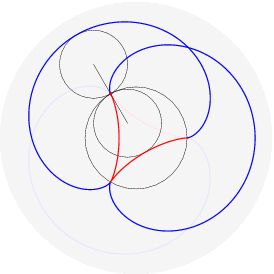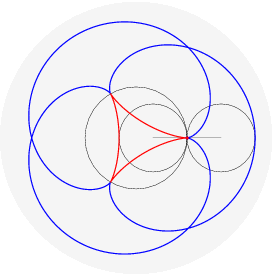
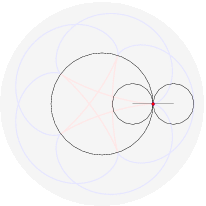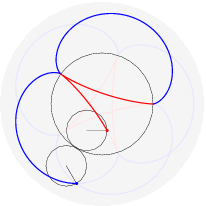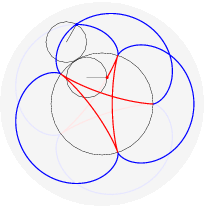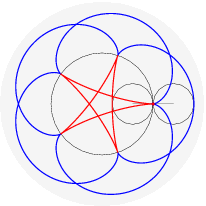
nelle figure per uno stesso rapporto sono disegnati sia l'epicicloide, sia l'ipocicloide: 1/1, 1/2, 1/3, 1/4, 1/5, 2/1, 2/3, 2/5, 3/1, 3/2, 3/4, 3/5, 4/3, 4/5, 5/2, 5/3, 5/4, 5/6, 6/5. Qualche esempio di cerchi osculatori e curva dei centri osculatori (di coniche):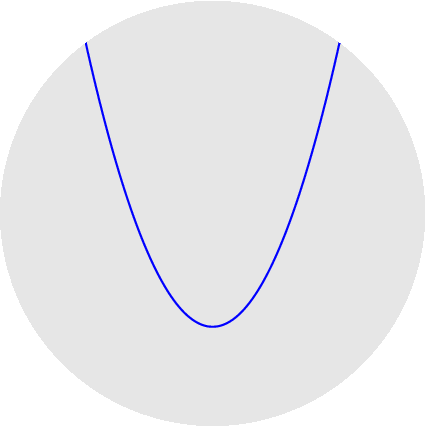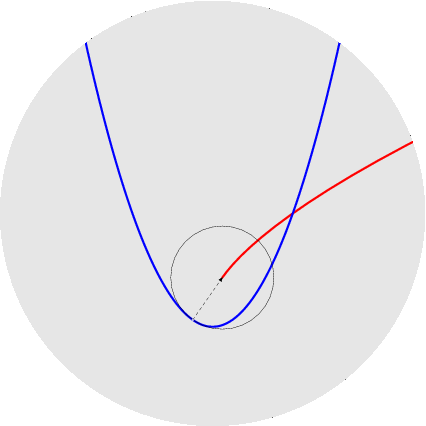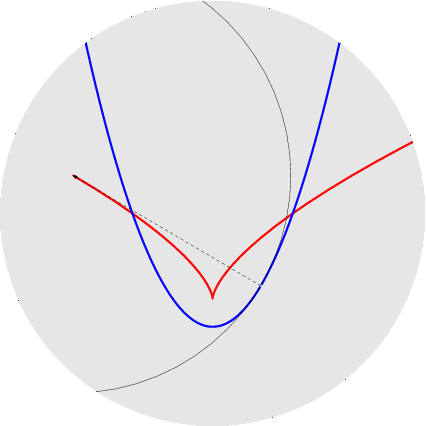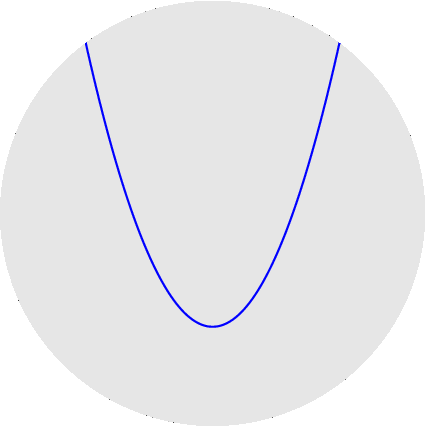 
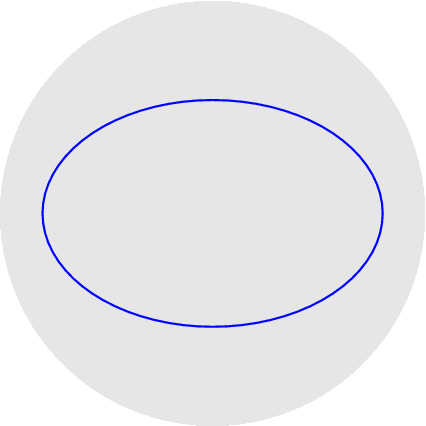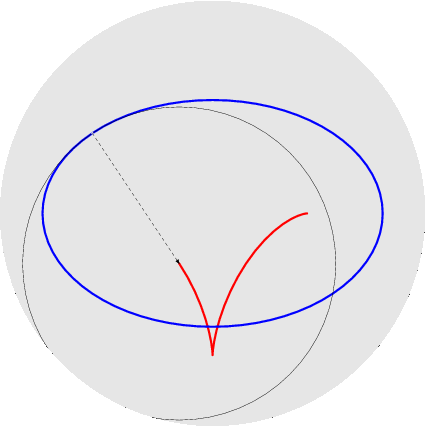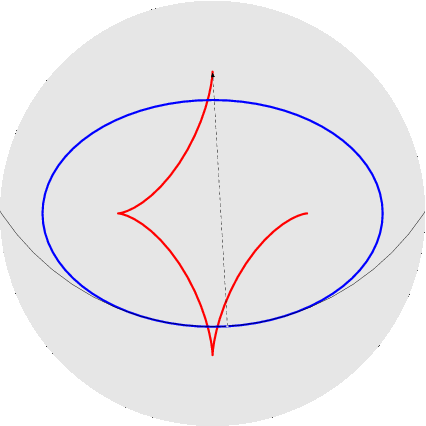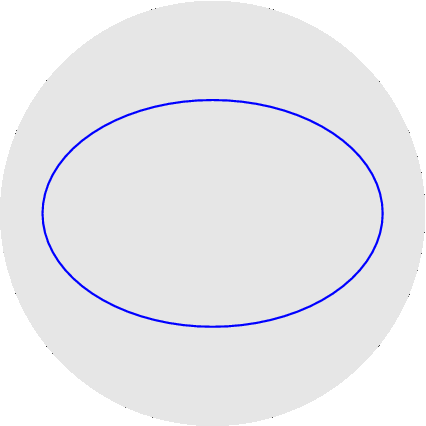
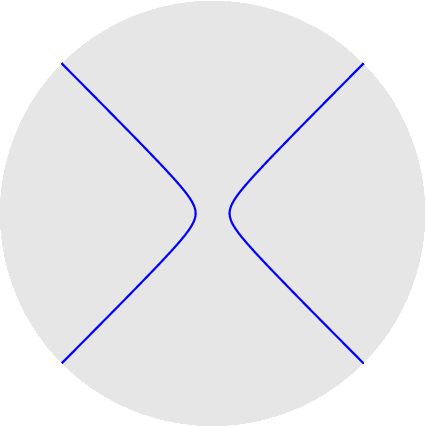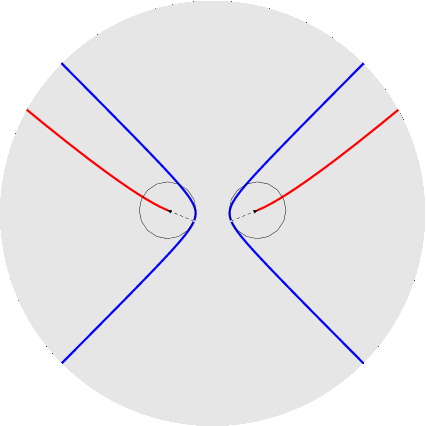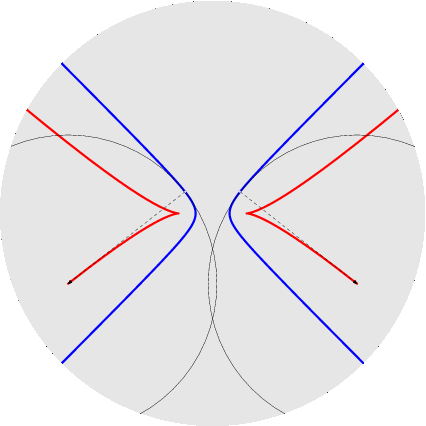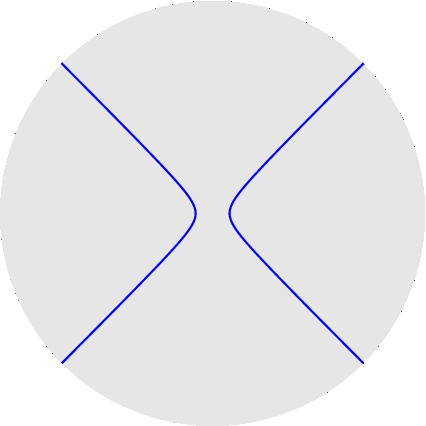
Per non appesantire la pagina metto semplicemente i link ad altri esempi: cicloide, seno, seno iperbolico, coseno iperbolico, spirale di Archimede, eliche circolari. ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ Tutti conoscono l'immersione del toro (quadrato con i lati opposti opportunamente identificati) nello spazio tridimensionale, con l'effetto pero` di deformare le lunghezze (i paralleli tutti uguali tra loro, i meridiani no); si puo` invece immergere in R^4 senza deformazioni (toro piatto): qui si vede cosa succede di un reticolo regolare di punti sul quadrato: 
(varie proiezioni da R^4 sul foglio) e qui cosa succede di meridiani e paralleli (si vede bene che non e` il toro tridimensionale); la figura e` piuttosto pesante (circa 6Mb). Il piano proiettivo reale si ottiene anch'esso identificando opportunamente i lati di un quadrato, oppure i punti antipodali di un disco, ma e` una superficie che non si puo` immergere nello spazio tridimensionale senza autointersezioni (ma in R^4 si`). Qui abbiamo dei filmati di immersioni ingenue in R^3 (un disco nel piano XZ viene fatto ruotare di a/2 attorno a X, e di a attorno a Z: questo da` una superficie di cui si vedono varie proiezioni qui) e in R^4 (seconda rotazione attorno al quarto asse: diverse viste qui e qui). Tutti i file sono abbastanza pesanti (circa 5Mb), ma da alcuni fotogrammi si intravvedono le proiezioni delle costruzioni classiche delle superficie di Boy e di quella romana di Steiner. - si introducono le nozioni di base di topologia (aperti, chiusi, funzioni continue, assiomi di separazione, connessione, compattezza...), e infine si studia la classificazione topologica delle superficie reali compatte. ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ Tutti conoscono la costruzione dell'insieme di Cantor: 
Esempi di insiemi di Cantor 2-dimensionali: 
Cubo di Menger e complementare: 
|
|
Orari del corso Parte A (primo semestre 30 settembre 2024 - 18 gennaio 2025): Lunedì 14.30-16.15, Martedì 14.30-16.15, Giovedì 15.30-17.15. Aula 1A/150 (Torre Archimede); Parte B (secondo semestre 24 febbraio 2025 - 12 giugno 2025): da decidere |
|
Qui di seguito si potranno trovare gli appunti del corso; si tratta di note non definitive, soggette a variazioni (inoltre sono spesso sovrabbondanti rispetto a quanto sarà effettivamente svolto a lezione). Chi trovasse errori di stampa, inesattezze o altro è pregato di comunicarmeli; anche i commenti sono ben accetti. NOTA : tutti questi file saranno aggiornati a fine settembre 2024 ! (A) Per Geometria 2 parte A: si puo` seguire la seconda parte di AGLQ (Algebra e Geometria Lineari e Quadratiche) in cui vi sono quattro capitoli (Forme bilineari, quadratiche ed hermitiane, Coniche e Quadriche, Geometria di Minkowski, Geometrie Piane non-Euclidee); purtroppo per mancanza di tempo mancano ancora i capitoli sulle geometrie tridimensionali non euclidee e sull'algebra multilineare... per chi preferisse altri riferimenti, e` circa equivalente usare gli appunti corrispondenti di M.Candilera. (B) Per Geometria 2 parte B: gli argomenti del corso sono una parte degli appunti G&Te (i primi 4 capitoli, tranne alcuni punti, gli altri argomenti appartengono al corso di Topologia del terzo anno, ma ho preferito lasciarli perche' legati ai nostri argomenti); > per la parte di geometria differenziale di curve e superficie si possono consultare i primi capitoli del libro di Do Carmo ("differential geometry of curves and surfaces"), o anche i primi capitoli del libro di Klingenberg ("A course in Differential Geometry"). > per la parte di topologia generale si puo` fare riferimento anche, per esempio, a: Checcucci-Tognoli-Vesentini (Lezioni di topologia generale), Tullio Valent (appunti ciclostilati di Istituzioni di Analisi Superiore a.a.75/76 rivisti, primi due paragrafi). (P) Il programma dettagliato dell'orale (a.a. 2019/20): pdf (verra` aggiornato a fine anno). (E) Si cerchera` di rendere disponibili i testi degli esami degli anni precedenti: ecco un file pdf (nota: ho aggiunto qualche suggerimento/risultato negli appunti per geometria differenziale e topologia, ma consiglierei di provare da soli a risolvere gli esercizi prima); altri si possono trovare (qualcuno risolto) nell'archivio appunti, tra gli esami 'storici'. |
|
Qui di seguito si troveranno date, risultati e testi degli esami di Geometria 2. Ricordiamo che durante gli esami scritti non puo` essere consultato alcun tipo di materiale tranne un foglio protocollo personale in cui possono essere riportate le formule ritenute utili della parte di geom.diff. Non è consentito l'uso di dispense, libri, enciclopedie, appunti personali, e naturalmente nemmeno l'uso di strumenti quali calcolatrici, computer, telefonini, compagni di corso, amici, ecc. L'orale sara` obbligatorio per tutti gli studenti (domande su definizioni ed enunciati su tutto il programma del corso; saper esporre le dimostrazioni fondamentali che saranno indicate nel programma); vi si accede avendo una valutazione positiva sulle due parti del corso (ottenute con compitini e/o appelli) ed e` unico; terminato l'orale si propone un voto finale tenendo conto degli scritti nelle due parti e dell'orale stesso. Date compitini: 25 novembre, PP1-G2A-2024.pdf (PP1-G2A-2024-s.pdf) 17 gennaio, PP2-G2A-2024.pdf (PP2-G2A-2024-s.pdf) 28 aprile, 12 giugno Date appelli (scritti): 29 gennaio (solo parte A) A1-G2A-2024.pdf (A1-G2A-2024-s.pdf) 19 febbraio (solo parte A) A1R-G2A-2024.pdf (A1R-G2A-2024-s.pdf) 25 giugno 14 luglio 25 agosto 12 settembre NOTA: per gli orali ci saranno liste di iscrizione sulla pagina moodle del corso. se ci sono pochi studenti si fanno in ufficio, altrimenti si prenotera` un'aula; l'orale consiste in 4 domande, 2 sulla parte A e due sulla parte B del programma; e` necessario conoscere definizioni ed enunciati del programma; per aumentare il voto rispetto agli scritti e` necessario saper esporre le dimostrazioni del programma, o saper rispondere a qualche domanda inerente gli argomenti del corso. Il voto finale puo` variare di qualche punto rispetto ai punteggi degli scritti, e non e` la media pesata di alcunche'. NOTA: in linea di massima i risultati degli esami scritti vengono inseriti nella pagina moodle, e non in UniWeb che useremo solo per la registrazione del voto finale; e` buona norma venire a ritirare i propri compiti, in modo da vedere gli errori commessi ed evitare di ripeterli in futuro... |
|
Considerazioni finali su corso ed esami (anno 2014/15): il programma di Geometria 2 e` piuttosto intensivo rispetto al numero di ore a disposizione per svilupparlo, specie nel secondo semestre, in cui al mattino c'e` spazio per pochi esempi/esercizi, e si usano le ore pomeridiane per studiare esempi importanti per avere una buona comprensione degli argomenti trattati (si tratta comunque di esempi, cioe` quel tipo di 'applicazioni delle definizioni' che ci si puo` aspettare che gli studenti del secondo anno sappiano fare con un po' di autonomia). Mentre le parti piu` standard (geometria proiettiva, coniche e quadriche, curve e superficie diferenziali) sono piu` facilmente seguite, o si prestano meglio ad un apprendimento meccanico, la parte di topologia si dimostra sempre qualitativamente diversa. E` vero che c'e` poco tempo a disposizione (ma non che gli altri argomenti abbondassero di tempo...), e` vero che si tratta di nozioni in parte o in casi particolari gia` incontrate in analisi (ma questo non sembra aiutare molto...), ma si nota sempre nella parte di topologia degli esami uno iato tra chi fa bene e chi fa molto poco o commette molti errori. Come ho detto a lezione, la mia impressione e` che negli argomenti di topologia sia essenziale formarsi una 'nuova' intuizione usando le definizioni e controllando i risultati in molti esempi diversi, e qui non aiuta molto la passivita` di veder fatti gli esempi: o si prova a ragionarci da soli, oppure e` difficile sviluppare questo 'nuovo senso'. Prima o poi scrivero` qualche soluzione degli esami, ma per il momento ho poco tempo; e sono anche convinto che lasciare che ciascuno debba trovarsi una soluzione sia una buona strategia... Aggiornamento (anno 2015/16): sono stato convinto dagli eventi che scrivere alcuni 'risultati' degli esami di topologia generale sia utile, e li ho inseriti nell'aggiornamento del file G&Te. Aggiunta: Sono stato ad una riunione/conferenza per i 'nuovi metodi didattici', in cui qualcuno spiegava cosi` le lezioni 'tradizionali': il docente copia dal libro alla lavagna, gli studenti copiano dalla lavagna al quaderno, e in tutto questo non si usa il cervello dello studente (e, io sospetto, nemmeno quello del docente). Sono d'accordo che se uno fa lezione all'universita` copiando da un libro, e` buona cosa che provi a cambire metodo di insegnamento (ma troverei imbarazzante che il nuovo metodo sia far fare lezione agli studenti). Forse mi e` capitato di avere qualche vecchio docente che recitava il proprio o qualche altrui libro, ma devo dire che per fortuna mi sembrano eccezioni nel campo della matematica; e in particolare io non ho mai inteso che una lezione sia la recita di un libro, e nemmeno dei miei appunti... La lezione dovrebbe servire per trasmettere le idee importanti e mettere l'accento sulle cose nuove da imparare e come sono collegate con le cose gia` note; questo e` difficile ottenerlo leggendo un libro... Aggiornamento (anno 2016/17): Visto che alcuni rappresentanti degli studenti avevano dichiarato in una riunione della CPDS della Scuola di Scienze che tutti gli studenti di matematica preferivano l'uso del tablet rispetto all'uso della lavagna, ho chiesto agli studenti del corso di indicare la loro preferenza tra queste possibilita`: dalle risposte ho contato 10 preferenze per il tablet, 15 indifferenti e 30 preferenze per la lavagna. Devo ammettere che io ho una preferenza per la lavagna: scrivere su un tablet, a parte che rende piu` noiose le lezioni, ha lo svantaggio di avere "meno spazio" per vedere piu` cose contemporaneamente e cercare di spiegare/capire le idee di base e le relazioni tra queste. E` vero che si rischia di andare piu` veloci, ma penso che per il momento continuero` ad usare la lavagna. Soprattutto perche' mi sembra che le lezioni debbano servire per trasmettere le idee di base, e nel caso siano nuove le tecniche di dimostrazione, per permettere poi di leggere meglio un testo su quegli argomenti, anche non necessariamente scritto dal docente; trasformare queste in un ulteriore file pdf da leggere mi sembra eccessivo: le lezioni non servono per produrre un ulteriore libro, ma per mettere in grado di capire i libri su quell'argomento... Aggiornamento (anno 2017/18): Quest'anno alla CPDS della Scuola di Scienze, sulla base di un questionario organizzato dai rappresentanti degli studenti, e` stato detto che il 60% degli studenti di matematica preferisce l'uso dei 'dispositivi multimediali' (20% preferisce la lavagna e 20% dipende/indifferente, per un totale di circa 120 questionari). Alla stessa domanda fatta nel corso di Geometria 2 ho avuto, su 52 questionari compilati, 10 preferenze per il tablet, 10 indifferenti, 32 per la lavagna. Avevo chiesto anche chi avesse compilato il questionario on-line dei rappresentanti: e` risultato che 17 studenti l'avevano compilato e 35 no (di cui 20 non sapevano che ci fosse stato). Secondo me la risposta generale dovrebbe essere sempre "dipende dal corso e dal docente"; ho concluso anche che il campione di chi risponde ad un questionario on-line e` piu` propenso a preferire cose multimediali. Alla domanda "se non fosse obbligatorio, avreste seguito lo stesso questo corso?" le risposte sono state 3 'no' e 47 'si'. La critica piu` frequente riguarda l'assenza di esami/esercizi completamente svolti e qualche volta di dimostrazioni dettagliate di certi argomenti; un po' alla volta, man mano che mi rendo conto di cosa viene considerato un ostacolo, cerco di rimediare aumentando o riorganizzando il file degli appunti: comunque resto sempre dell'idea che gli argomenti trattati possono essere assimilati solo con un buon lavoro personale, trovare tutto scritto nei dettagli da` solo l'illusione di aver capito; la sicurezza che un risultato o un ragionamento sia giusto puo` darla solo il fatto di controllare di aver usato definizioni e risultati in modo corretto, ed e` uno stato che e` meglio raggiungere da soli, eventualmente con qualche suggerimento, ma non leggendo una soluzione gia` fatta (spesso ci sono vari modi di risolvere un problema, non ce n'e` uno solo corretto). Aggiornamento (anno 2018/19): Alla solita domanda quest'anno ho ricevuto 6 'no', 2 astensioni e 38 'si'. Ho avuto anche piu` commenti del solito, di cui cerchero` di tenere conto. Mi resta anche l'impressione di non aver mai avuto un cosi` grande iato tra l'impressione generale della classe e dell'interesse mostrato durante le lezioni, e i risultati delle prove parziali, specie nel secondo semestre, con quasi tutta la classe bloccata davanti a difficolta` che insisto a ritenere ragionevoli. Mi spiego questi risultati solo cosi`: che si studia solo in modo locale e settoriale, e appena si chiede di usare qualcosa del primo anno o di altri corsi casca il palco. Una visione piu` generale delle cose che si studiano e` essenziale, altrimenti si sapranno risolvere solo i problemi che sono gia` stati risolti, e neanche tutti perche' uno se li dimentica... |
